Proyecciones ortogonales
La proyección ortogonal de un punto P sobre una recta r es el punto donde la perpendicular trazada desde P corta a la recta.
Por ejemplo, consideremos un punto P y una recta r.
La proyección ortogonal es el punto P', donde la perpendicular desde P intersecta la recta r.
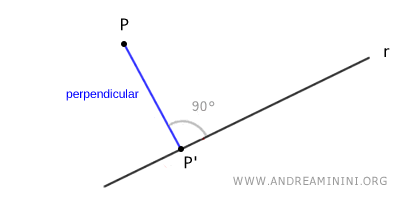
En este caso, la proyección ortogonal de P sobre r es el punto P'.
El segmento \( PP' \), que une el punto con su proyección, representa la distancia más corta entre P y la recta.
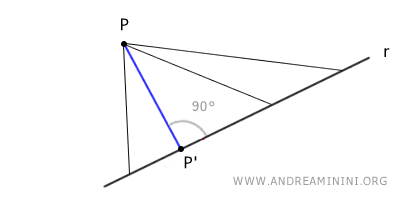
Por un punto exterior a una recta pasa una única perpendicular. Es decir, existe una sola recta perpendicular a r que pasa por P.
Una perpendicular es una recta o segmento que pasa por un punto y corta a otra formando un ángulo recto (90°). En el plano, representa la menor distancia entre el punto y la recta.
Demostración
Para demostrar la existencia y unicidad de la perpendicular desde un punto P a una recta r, consideremos dos puntos A y B equidistantes del pie de la perpendicular, de modo que \( AP' \cong BP' \).
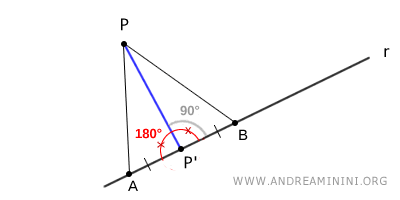
La perpendicular corta a r en un ángulo recto y biseca el ángulo llano \( \angle A\hat{P'}B = 180^\circ \).
Como un ángulo llano solo admite una única bisectriz, la perpendicular desde P a r debe ser única.
Proyección ortogonal de un segmento
El procedimiento para proyectar ortogonalmente un segmento es similar.
Supongamos que tenemos el segmento AB y la recta r.
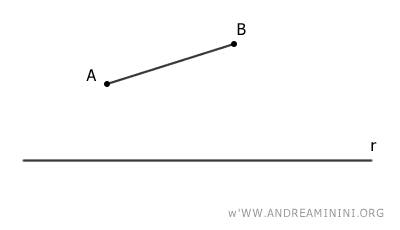
Proyectamos ortogonalmente los extremos A y B sobre la recta y unimos sus proyecciones.
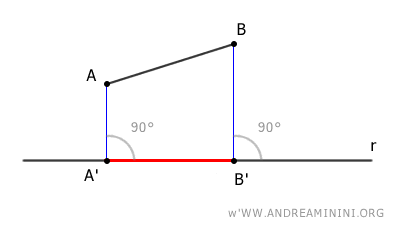
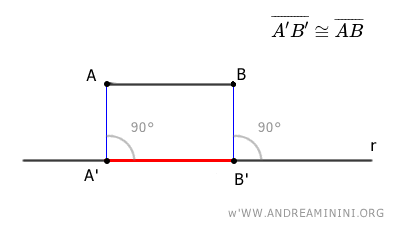
Así, la proyección ortogonal del segmento AB sobre r es el segmento A'B'.
Nota: La proyección ortogonal A'B' de un segmento sobre una recta es congruente con el segmento AB únicamente cuando el segmento es paralelo a la recta.
En todos los demás casos, la longitud de la proyección ortogonal es siempre menor que la del segmento original: $$ \overline{A'B'} \le \overline{AB} $$ En el caso particular en que el segmento es perpendicular a la recta, su proyección ortogonal se reduce a un solo punto.
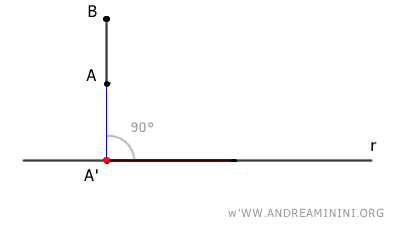
Y así sucesivamente.