Ecuación de la Recta que Pasa por Dos Puntos

La ecuación de una recta que pasa por dos puntos distintos \( (x_1, y_1) \) y \( (x_2, y_2) \) en el plano se puede determinar mediante la siguiente fórmula: $$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$ Por dos puntos distintos en el plano pasa una única recta.

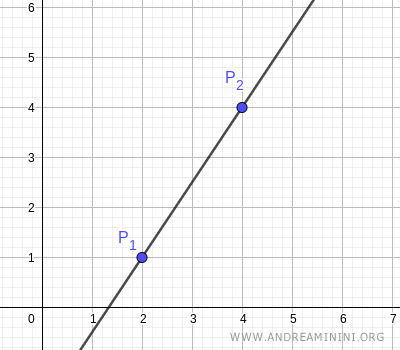
Si en lugar del plano estamos en el espacio tridimensional, para dos puntos distintos \( (x_1, y_1, z_1) \) y \( (x_2, y_2, z_2) \), la ecuación de la recta que los une se expresa así: $$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} = \frac{z - z_1}{z_2 - z_1} $$ lo que también se puede escribir de forma equivalente: $$ \begin{cases} \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} \\ \\ \frac{y - y_1}{y_2 - y_1} = \frac{z - z_1}{z_2 - z_1} \end{cases} $$ siempre que los puntos sean distintos, es decir, $ x_1 \ne x_2 $, $ y_1 \ne y_2 $ y $ z_1 \ne z_2 $.

A esta representación se la conoce como la forma fraccionaria de la ecuación de la recta.

Se puede emplear para deducir la ecuación de la recta en la forma general:

$$ ax + by + c = 0 $$

También recibe el nombre de condición de colinealidad, ya que permite verificar si tres puntos \( (x, y) \), \( (x_1, y_1) \) y \( (x_2, y_2) \) se hallan alineados sobre la misma recta.

• Si el punto $ (x, y) $ satisface esta proporción, entonces pertenece a la recta determinada por $ (x_1, y_1) $ y $ (x_2, y_2) $.
• Si no la cumple, el punto no es colineal con los otros dos.

Ejemplo

Queremos hallar la ecuación de la recta que pasa por dos puntos distintos A y B en el plano.

El punto A tiene coordenadas \( (x_1, y_1) = (1, 2) \) y el punto B está en \( (x_2, y_2) = (4, 5) \).

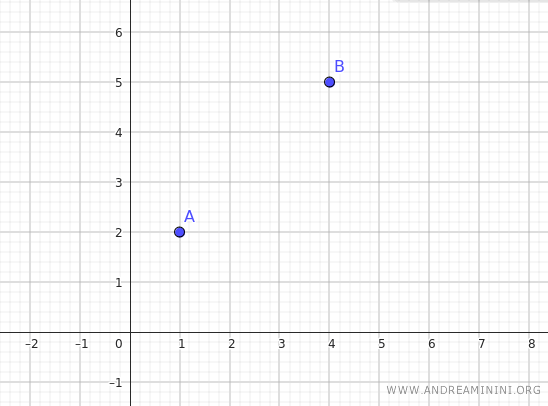
Aplicamos la fórmula de la recta que pasa por dos puntos:

$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$

En este caso, los valores son \( x_1 = 1 \), \( y_1 = 2 \) y \( x_2 = 4 \), \( y_2 = 5 \).

$$ \frac{y - 2}{5 - 2} = \frac{x - 1}{4 - 1} $$

$$ \frac{y - 2}{3} = \frac{x - 1}{3} $$

Multiplicando ambos lados por 3, simplificamos la ecuación:

$$ \frac{y - 2}{3} \cdot 3 = \frac{x - 1}{3} \cdot 3 $$

$$ y - 2 = x - 1 $$

Reordenamos los términos para obtener la forma implícita:

$$ y - 2 - x + 1 = 0 $$

$$ y - x - 1 = 0 $$

Así, obtenemos la ecuación implícita de la recta: y - x - 1 = 0, que pasa por los puntos (1, 2) y (4, 5).

Para expresarla en forma explícita, despejamos y en función de x:

$$ y = x + 1 $$

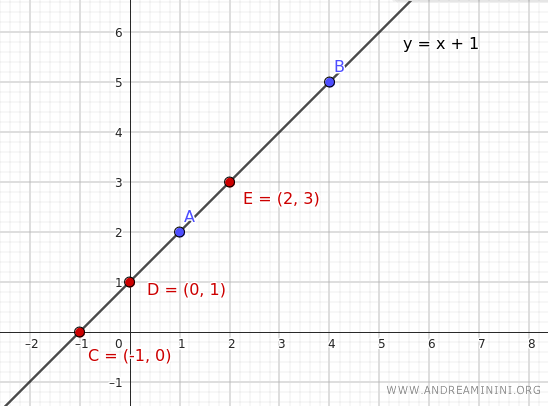
Podemos comprobarlo asignando diferentes valores a la variable independiente x y obteniendo los correspondientes valores de y:

$$ \begin{array}{c|c} x & y = x + 1 \\ \hline -1 & 0 \\ 0 & 1 \\ 1 & 2 \\ 2 & 3 \end{array} $$

Esto nos proporciona varios puntos que se encuentran sobre la recta.

 

Solución Alternativa

Otra forma de resolverlo es calcular la pendiente (m) de la recta a partir de las coordenadas de los dos puntos. La pendiente se obtiene con:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

Esta fórmula indica cuánto se “eleva” o “desciende” la recta al desplazarse de izquierda a derecha a lo largo del eje x.

Con los valores \( x_1 = 1 \), \( y_1 = 2 \), y \( x_2 = 4 \), \( y_2 = 5 \):

$$ m = \frac{5 - 2}{4 - 1} $$

$$ m = \frac{3}{3} $$

$$ m = 1 $$

Una vez conocida la pendiente, podemos usar la ecuación punto-pendiente:

$$ y - y_1 = m \cdot (x - x_1) $$

Sustituyendo \( m = 1 \):

$$ y - y_1 = 1 \cdot (x - x_1) $$

$$ y - y_1 = x - x_1 $$

Con \( x_1 = 1 \) y \( y_1 = 2 \):

$$ y - 2 = x - 1 $$

Despejamos y para obtener la ecuación explícita:

$$ y = x - 1 + 2 $$

$$ y = x + 1 $$

Como era de esperar, el resultado coincide.

Por ejemplo, la ecuación de la recta que pasa por los puntos \( (1, 2) \) y \( (3, 8) \) sería \( y = 3x - 1 \).

Ejemplo 2

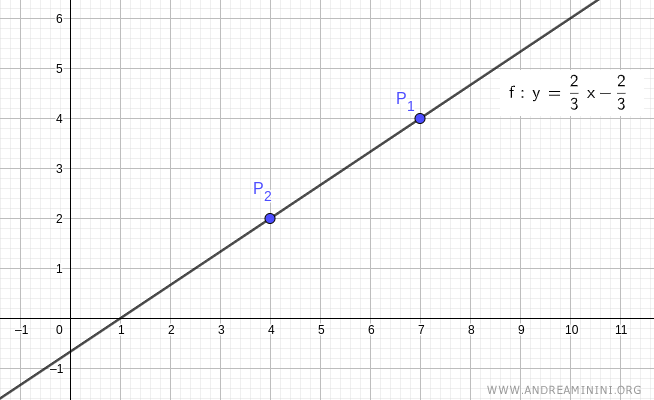
Consideremos dos puntos distintos en el plano: P₁(7,4) y P₂(4,2).

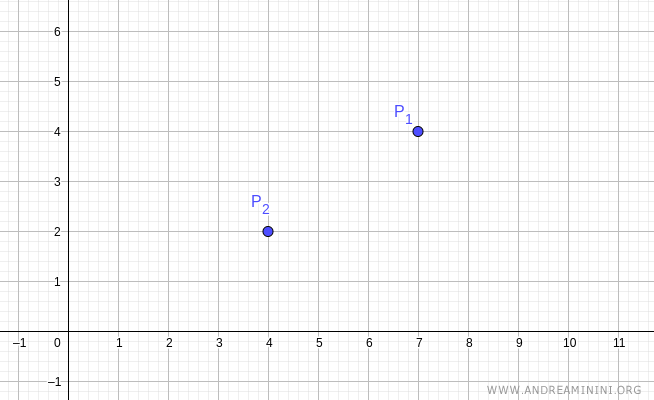
La ecuación de la recta que pasa por los puntos P₁ y P₂ es:

$$ \frac{x - x_1}{x_2 - x_1} = \frac{y - y_1}{y_2 - y_1} $$

En este caso, (x₁, y₁) = (7,4) y (x₂, y₂) = (4,2).

Sustituyendo los valores \( x_1 = 7 \), \( x_2 = 4 \), \( y_1 = 4 \) y \( y_2 = 2 \), obtenemos:

$$ \frac{x - 7}{4 - 7} = \frac{y - 4}{2 - 4} $$

$$ \frac{x - 7}{-3} = \frac{y - 4}{-2} $$

Procedemos ahora a despejar y:

$$ \frac{x}{-3} + \frac{-7}{-3} = \frac{y}{-2} + \frac{-4}{-2} $$

$$ \frac{y}{-2} = \frac{x}{-3} + \frac{-7}{-3} - 2 $$

$$ y = (-2) \cdot \left[ \frac{x}{-3} + \frac{7 - 6}{3} \right] $$

$$ y = (-2) \cdot \left[ \frac{x}{-3} + \frac{1}{3} \right] $$

$$ y = \frac{2}{3}x - \frac{2}{3} $$

Esta es la ecuación explícita de la recta que pasa por los puntos P₁(7,4) y P₂(4,2).

Al variar el valor de x, podemos encontrar todos los puntos que se sitúan sobre dicha recta.

Ejemplo 3

Consideremos ahora tres puntos en el plano:

$$ A(1,2), \quad B(3,6), \quad C(5,10). $$

Queremos determinar si los puntos $A$, $B$ y $C$ son colineales.

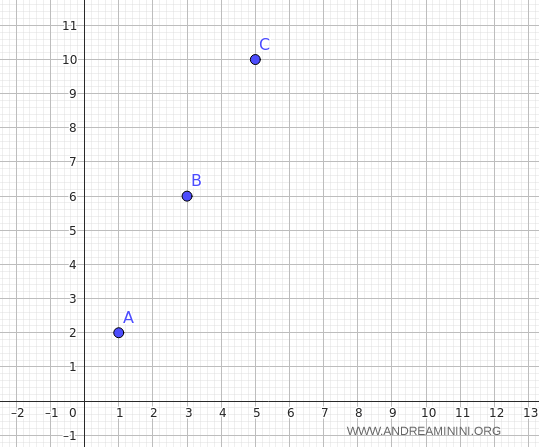
Para comprobarlo, podemos recurrir a la forma fraccionaria de la ecuación de la recta.

Primero, consideremos los puntos $A$ y $B$:

$$ x_1 = 1, \; y_1 = 2, \quad x_2 = 3, \; y_2 = 6. $$

La condición para que el punto $C(x,y) = (5,10)$ se encuentre en la misma recta que $A$ y $B$ es:

$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$

Sustituyendo las coordenadas, se obtiene:

$$ \frac{10 - 2}{6 - 2} = \frac{5 - 1}{3 - 1} $$

$$ \frac{8}{4} = \frac{4}{2} \quad \Rightarrow \quad 2 = 2 $$

Dado que la igualdad se cumple, los tres puntos son colineales. Es decir, existe una única recta que pasa por todos ellos.

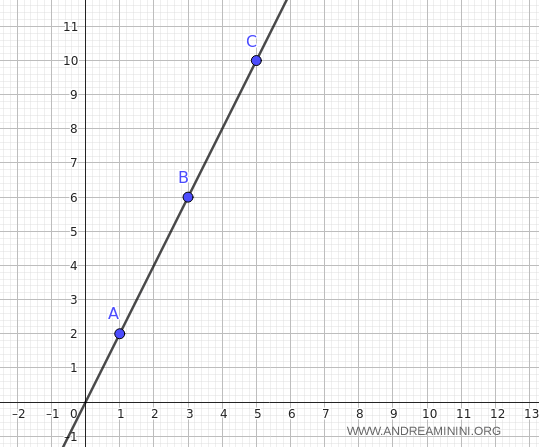
¿Cuál es la ecuación de esta recta? Vamos a determinarla utilizando los puntos $$ A(1,2) $$ y $$ B(3,6) $$. Primero calculamos la pendiente \( m \): $$ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2 $$ A continuación, escribimos la ecuación en forma punto-pendiente a partir del punto $A(1,2)$: $$ y - y_1 = m(x - x_1) $$ Sustituyendo los valores: $$ y - 2 = 2(x - 1) $$ Simplificando: $$ y = 2(x - 1) + 2 $$ $$ y = 2x - 2 + 2 $$ $$ y = 2x $$ Así, la ecuación explícita de la recta que pasa por los tres puntos es $ y = 2x $. Para expresarla en forma general \( ax + by + c = 0 \), reordenamos términos: $$ y - 2x = 0 $$ Opcionalmente, podemos multiplicar por $ -1 $ para que el coeficiente de $ x $ sea positivo: $$ 2x - y = 0 $$ Por tanto, la ecuación en forma general (implícita) de la recta es: $$ 2x - y = 0 $$

Solución alternativa

Otra forma de comprobar la colinealidad es comparar las pendientes.

Primero, calculamos la pendiente \( m_{AB} \):

$$ m_{AB} = \frac{6 - 2}{3 - 1} = \frac{4}{2} = 2 $$

Luego, calculamos la pendiente \( m_{BC} \):

$$ m_{BC} = \frac{10 - 6}{5 - 3} = \frac{4}{2} = 2 $$

Como \( m_{AB} = m_{BC} \), los tres puntos están alineados sobre la misma recta.

Método 3 (Usando el área del triángulo). Una tercera forma de verificar la colinealidad consiste en calcular el área del triángulo $ABC$: $$ \text{Área} = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| $$ Sustituyendo los valores: $$ \begin{align} \text{Área} &= \frac{1}{2} \left| 1(6 - 10) + 3(10 - 2) + 5(2 - 6) \right| \\ &= \frac{1}{2} \left| -4 + 24 - 20 \right| \\ &= \frac{1}{2} \times 0 = 0 \end{align} $$ Dado que el área es cero, los puntos son colineales.

Ejemplo 4

Analicemos ahora dos puntos en el espacio tridimensional \( \mathbb{R}^3 \):

$$ P_1(1,2,3), \quad P_2(5,6,7) $$

Queremos encontrar la ecuación de la recta que pasa por los puntos $P_1$ y $P_2$.

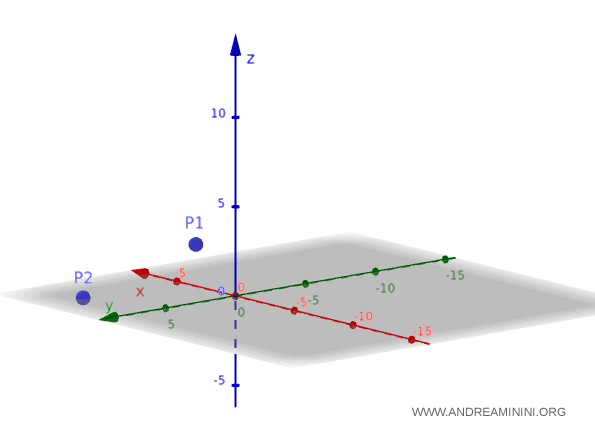
Planteamos el siguiente sistema de ecuaciones:

$$ \begin{cases} \dfrac{y - y_1}{y_2 - y_1} = \dfrac{x - x_1}{x_2 - x_1} \\ \\ \dfrac{y - y_1}{y_2 - y_1} = \dfrac{z - z_1}{z_2 - z_1} \end{cases} $$

Sustituyendo las coordenadas de $ P_1(1,2,3) $ y $ P_2(5,6,7) $, tenemos:

$$ \begin{cases} \dfrac{y - 2}{6 - 2} = \dfrac{x - 1}{5 - 1} \\ \\ \dfrac{y - 2}{6 - 2} = \dfrac{z - 3}{7 - 3} \end{cases} $$

$$ \begin{cases} \dfrac{y - 2}{4} = \dfrac{x - 1}{4} \\ \\ \dfrac{y - 2}{4} = \dfrac{z - 3}{4} \end{cases} $$

Multiplicamos ambos lados de cada ecuación por 4 y simplificamos:

$$ \begin{cases} y - 2 = x - 1 \\ \\ y - 2 = z - 3 \end{cases} $$

Despejando x e y, obtenemos:

$$ \begin{cases} x = y - 1 \\ \\ y = z - 1 \end{cases} $$

Por lo tanto, la recta se describe mediante el siguiente sistema reducido:

$$ \begin{cases} x = y - 1 \\ \\ y = z - 1 \end{cases} $$

A continuación, se muestra una representación gráfica de la recta que pasa por los puntos $ P_1 $ y $ P_2 $ en el espacio tridimensional.

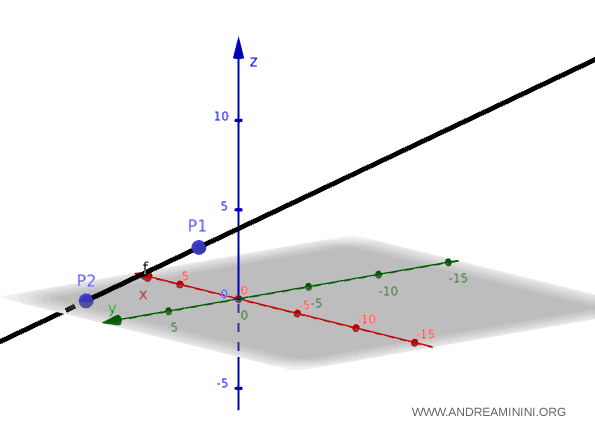
Nota. Para verificar si un punto, como $ Q(9,10,11) $, pertenece a la recta, basta con sustituir sus coordenadas en el sistema y comprobar si se cumplen las igualdades: $$ \begin{cases} x = y - 1 \\ \\ y = z - 1 \end{cases} $$ $$ \begin{cases} 9 = 10 - 1 \\ \\ 10 = 11 - 1 \end{cases} $$ $$ \begin{cases} 9 = 9 \\ \\ 10 = 10 \end{cases} $$ Dado que ambas igualdades se cumplen, el punto $ Q $ pertenece a la recta.

Demostración

Para demostrar la fórmula de la recta que pasa por dos puntos, consideremos tres puntos en el plano: \( (x_1, y_1) \), \( (x_2, y_2) \) y \( (x, y) \).

Suponemos que dichos puntos se hallan sobre la misma recta.

Por lo tanto, podemos plantear el siguiente sistema de ecuaciones:

$$ \begin{cases} ax_1 + by_1 + c = 0 \\ ax_2 + by_2 + c = 0 \\ ax + by + c = 0 \end{cases} $$

Aplicando el método de reducción, restamos la primera ecuación de la segunda y de la tercera:

$$ \begin{cases} a(x_2 - x_1) + b(y_2 - y_1) = 0 \\ a(x - x_1) + b(y - y_1) = 0 \end{cases} $$

$$ \begin{cases} a(x_2 - x_1) = - b(y_2 - y_1) \\ a(x - x_1) = - b(y - y_1) \end{cases} $$

$$ \begin{cases} \frac{x_2 - x_1}{y_2 - y_1} = - \frac{b}{a} \\ \frac{x - x_1}{y - y_1} = - \frac{b}{a} \end{cases} $$

Comparando estas dos expresiones, se advierte que ambas equivalen a \(-b/a\).

De ello se deduce la siguiente igualdad:

$$ \frac{x_2 - x_1}{y_2 - y_1} = \frac{x - x_1}{y - y_1} $$

Finalmente, tras un sencillo paso algebraico, se obtiene la condición de colinealidad:

$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$

Esto concluye la demostración de la fórmula para la ecuación de la recta que pasa por dos puntos distintos \( (x_1, y_1) \) y \( (x_2, y_2) \) en el plano.

Enfoque Alternativo

Analicemos ahora dos puntos distintos en el plano: P₁(x₁, y₁) y P₂(x₂, y₂).

Para deducir la ecuación de la recta que pasa por P₁, utilizaremos el concepto de haz de rectas.

$$ y - y_1 = m(x - x_1) $$

Aquí, \( m \) es la pendiente de la recta, que puede asumir infinitos valores, uno por cada posible inclinación de la recta, salvo el caso particular de las rectas paralelas al eje y.

La pendiente de la recta que pasa por los puntos P₁ y P₂ se determina mediante:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

Si sustituimos esta pendiente en la ecuación del haz de rectas que pasan por P₁, obtenemos:

$$ y - y_1 = m(x - x_1) $$

$$ y - y_1 = \frac{y_2 - y_1}{x_2 - x_1}(x - x_1) $$

Separando términos en ambos lados, se llega a:

$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$

Así se deduce la ecuación de la recta que pasa por dos puntos.

La Recta que Pasa por Dos Puntos en Álgebra Lineal

Otra forma de demostrar la ecuación de la recta que pasa por dos puntos consiste en abordarla desde el marco de la álgebra lineal.

Este método requiere conocimientos básicos sobre vectores y operaciones matriciales.

Demostración

Consideremos dos puntos en el plano:

$$ P_1 \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} \quad P_2 \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} $$

La recta que pasa por P₁ y P₂ puede describirse mediante el siguiente vector director \(\overrightarrow{P_1P_2}\):

$$ v_r \equiv \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \end{pmatrix} $$

Utilizando dicho vector director, podemos escribir la ecuación vectorial de la recta:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} + t \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \end{pmatrix} $$

De ella se derivan las ecuaciones paramétricas de la recta, tomando como punto inicial P₁:

$$ \begin{cases} x = x_1 + t \cdot (x_2 - x_1) \\ y = y_1 + t \cdot (y_2 - y_1) \end{cases} $$

Nota: Partir de P₂ conduciría a otro sistema de ecuaciones paramétricas, aunque el resultado geométrico sería el mismo. Por lo tanto, para esta demostración, se puede elegir cualquiera de las dos formulaciones: $$ \begin{cases} x = x_2 + t \cdot (x_2 - x_1) \\ y = y_2 + t \cdot (y_2 - y_1) \end{cases} $$

Para un punto genérico \( P \) situado sobre la recta, podemos construir el siguiente vector respecto a P₁:

$$ \overrightarrow{P_1P} = P - P_1 = \begin{pmatrix} x - x_1 \\ y - y_1 \end{pmatrix} $$

Este vector \(\overrightarrow{P_1P}\) ha de ser paralelo y proporcional al vector director \(\overrightarrow{P_1P_2}\), puesto que ambos comparten la misma dirección de la recta \( r \).

Por tanto, los vectores \(\overrightarrow{P_1P}\) y \(\overrightarrow{P_1P_2}\) deben ser linealmente dependientes.

Si colocamos ambos vectores como columnas de una matriz, el determinante de dicha matriz debe anularse:

$$ det \begin{pmatrix} x - x_1 & x_2 - x_1 \\ y - y_1 & y_2 - y_1 \end{pmatrix} = 0 $$

Al desarrollar el determinante, se obtiene:

$$ (x - x_1)\cdot(y_2 - y_1) - (x_2 - x_1)\cdot(y - y_1) = 0 $$

Mediante unos pasos algebraicos adicionales, se llega a la ecuación cartesiana de la recta:

$$ (x - x_1)\cdot(y_2 - y_1) = (x_2 - x_1)\cdot(y - y_1) $$

$$ \frac{x - x_1}{x_2 - x_1} = \frac{y - y_1}{y_2 - y_1} $$

Así se obtiene la fórmula general para la ecuación de la recta que pasa por dos puntos.

Con esto se concluye la demostración.

Ejemplo Práctico

Veamos un caso concreto con dos puntos en el plano: P₁ y P₂.

$$ P_1 \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} = P_1 \begin{pmatrix} 7 \\ 4 \end{pmatrix} $$

$$ P_2 \begin{pmatrix} x_2 \\ y_2 \end{pmatrix} = P_2 \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$

Su representación gráfica es la siguiente:

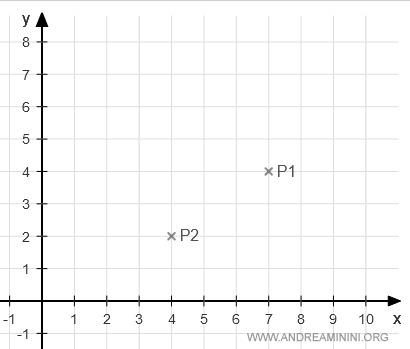
Si tomamos la dirección desde P₁ hacia P₂, obtenemos el vector \(\overrightarrow{P_1P_2}\):

$$ \overrightarrow{P_1P_2} = P_2 - P_1 = \begin{pmatrix} 4 \\ 2 \end{pmatrix} - \begin{pmatrix} 7 \\ 4 \end{pmatrix} = \begin{pmatrix} 4 - 7 \\ 2 - 4 \end{pmatrix} = \begin{pmatrix} -3 \\ -2 \end{pmatrix} $$

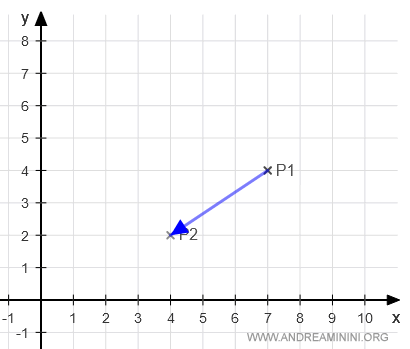
La ecuación vectorial de la recta es:

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \end{pmatrix} + t \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 7 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} 4 - 7 \\ 2 - 4 \end{pmatrix} $$

$$ \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 7 \\ 4 \end{pmatrix} + t \cdot \begin{pmatrix} -3 \\ -2 \end{pmatrix} $$

De ahí se obtiene la ecuación paramétrica de la recta:

$$ \begin{cases} x = 7 - 3t \\ y = 4 - 2t \end{cases} $$

Mediante esta ecuación paramétrica, es posible obtener cualquier punto de la recta variando el parámetro \( t \).

Así, un punto genérico sobre la recta puede expresarse como:

$$ P \begin{pmatrix} 7 - 3t \\ 4 - 2t \end{pmatrix} \quad \text{con} \quad t \in \mathbb{R} $$

Si \( t = 0 \), obtenemos el punto P₁, que es el origen del vector \(\overrightarrow{P_1P_2}\).

A medida que \( t \) aumenta, el punto se desplaza hacia P₂.

Cuando \( t = 1 \), se alcanza exactamente el punto P₂, extremo del vector \(\overrightarrow{P_1P_2}\).

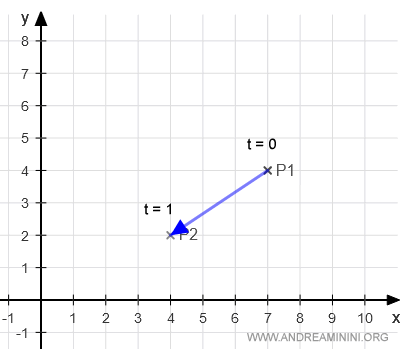
Veamos ahora cómo hallar la ecuación cartesiana.

La recta \( r \) pasa también por los puntos P₁ y P₂.

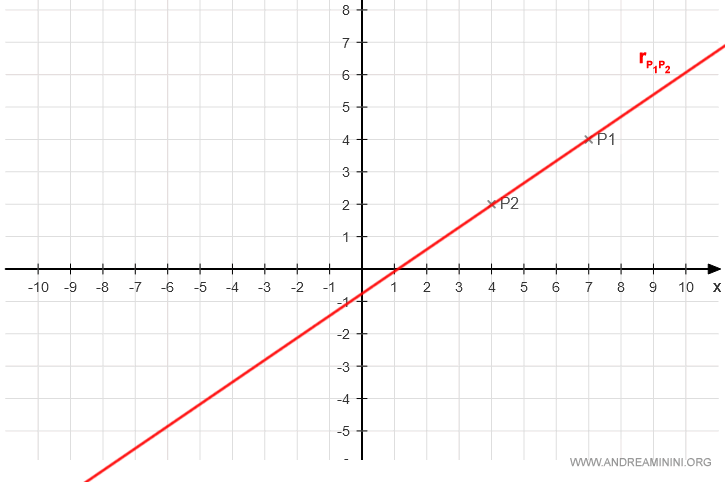
Para un punto genérico \( P \) en la recta \( r \):

$$ P \begin{pmatrix} x \\ y \end{pmatrix} $$

Los puntos P y P₁ determinan el vector \(\overrightarrow{P_1P}\):

$$ \overrightarrow{P_1P} = \begin{pmatrix} x \\ y \end{pmatrix} - \begin{pmatrix} 7 \\ 4 \end{pmatrix} $$

$$ \overrightarrow{P_1P} = \begin{pmatrix} x - 7 \\ y - 4 \end{pmatrix} $$

Este vector \(\overrightarrow{P_1P}\), que está contenido en la recta \( r \), es proporcional al vector geométrico \(\overrightarrow{P_2P_1}\) calculado previamente (es decir, \( v_r \)), ya que comparten la misma dirección.

$$ \overrightarrow{P_1P} = \begin{pmatrix} x - 7 \\ y - 4 \end{pmatrix} $$

$$ \overrightarrow{P_1P_2} = \begin{pmatrix} -3 \\ -2 \end{pmatrix} $$

Para que ambos vectores sean proporcionales, deben ser linealmente dependientes.

Para comprobarlo, el determinante de la matriz formada por estos vectores debe ser nulo:

$$ det \begin{pmatrix} x - 7 & -3 \\ y - 4 & -2 \end{pmatrix} = 0 $$

Calculando el determinante, obtenemos la ecuación cartesiana de la recta:

$$ (x - 7)(-2) - (-3)(y - 4) = 0 $$

$$ -2x + 14 + 3y - 12 = 0 $$

$$ -2x + 3y + 2 = 0 $$

Podemos despejar una variable en función de la otra:

$$ y = \frac{2x - 2}{3} $$

¿Por qué es útil conocer la ecuación cartesiana? Porque nos permite verificar si un punto con coordenadas (x, y) pertenece o no a la recta.

Y así sucesivamente.