Teorema de Tales

Cuando un conjunto de rectas paralelas corta dos rectas transversales, r y s, los segmentos determinados sobre ellas son directamente proporcionales.  $$ AB:CD = A'B':C'D' $$

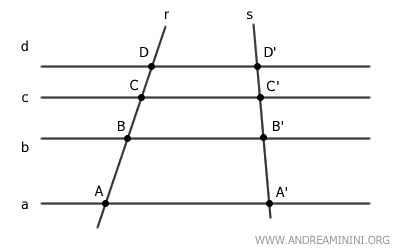
Por ejemplo, si sobre la transversal r tenemos los segmentos AB y CD, entonces en la transversal s existirán los segmentos correspondientes A'B' y C'D' que guardan la misma proporción. Es decir, AB está a CD como A'B' está a C'D'.

$$ AB:CD = A'B':C'D' $$

Esta relación expresa la proporcionalidad directa entre los pares de segmentos sobre ambas transversales.

Existe también la recíproca del teorema de Tales.

Si para cada par de segmentos AB y CD sobre una transversal r existe un par correspondiente A'B' y C'D' sobre otra transversal s tal que se cumple $$ AB:CD = A'B':C'D' $$, entonces las rectas que generan esas intersecciones son necesariamente paralelas.

El teorema de Tales y su recíproco proporcionan las condiciones necesarias y suficientes para que varias rectas sean paralelas, a partir del criterio de proporcionalidad directa.

El Teorema de Tales (o correspondencia de Tales) constituye un pilar fundamental de la geometría plana. Se atribuye tradicionalmente a Tales de Mileto, uno de los primeros matemáticos y filósofos griegos, aunque es probable que el principio ya fuera conocido en épocas anteriores.

Un ejemplo práctico

Consideremos un conjunto de rectas paralelas que intersectan dos transversales, r y s, en distintos puntos.

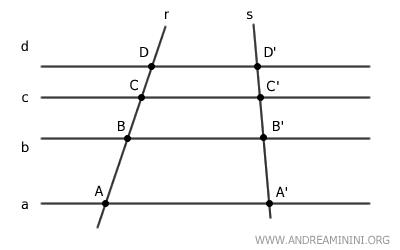
En esta configuración, los segmentos AB y CD sobre la recta r y sus correspondientes A'B' y C'D' sobre la recta s cumplen la proporción directa:

$$ AB:CD = A'B':C'D' $$

Es decir, el cociente entre las longitudes de los segmentos sobre una transversal es igual al cociente entre los segmentos correspondientes sobre la otra.

La recíproca del teorema de Tales

Si existen dos pares de segmentos AB y CD sobre una recta r, y A'B' y C'D' sobre otra recta s, tales que $$ AB:CD = A'B':C'D' $$ y además los segmentos AA' y BB' son paralelos, entonces los segmentos CC' y DD' también son paralelos.

Dicho de otra forma, si los extremos de los primeros segmentos se unen mediante rectas paralelas, y la proporción de longitudes se mantiene entre los pares, entonces las uniones de los extremos del segundo par también serán paralelas.

Ejemplo

Tomemos los segmentos AB y CD sobre la recta r, y los correspondientes A'B' y C'D' sobre la recta s.

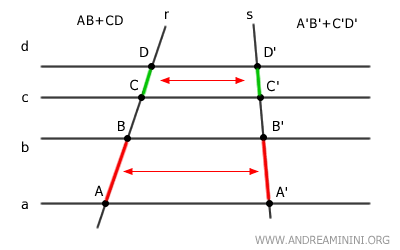
Se cumple la proporción:

$$ AB:CD = A'B':C'D' $$

Y los segmentos que conectan los extremos de los primeros pares son paralelos:

$$ AA' \parallel BB' $$

Entonces, según la recíproca del teorema de Tales, también se verifica:

$$ CC' \parallel DD' $$

Demostración

Supongamos que disponemos de un conjunto de rectas paralelas: a, b, c, d.

$$ a \parallel b \parallel c \parallel d $$

Y que dos transversales, r y s, cortan este conjunto de rectas.

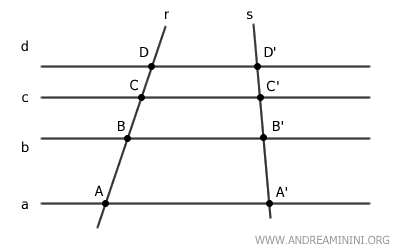
Queremos demostrar que para cualquier par de segmentos AB y CD sobre la transversal r, existen segmentos A'B' y C'D' sobre la transversal s tales que:

$$ AB:CD = A'B':C'D' $$

Denotamos por R el conjunto de segmentos sobre la recta r y por S los segmentos sobre la recta s:

$$ R = \{ \text{segmentos sobre r} \}, \quad S = \{ \text{segmentos sobre s} \} $$

Según un principio básico de la geometría, cada punto de intersección sobre la transversal r tiene un punto correspondiente sobre s, ya que ambas cortan al mismo conjunto de paralelas.

Es decir, existe una correspondencia biunívoca entre los puntos de r y los puntos de s.

Por ejemplo, al punto A le corresponde A', al punto B le corresponde B', etc.

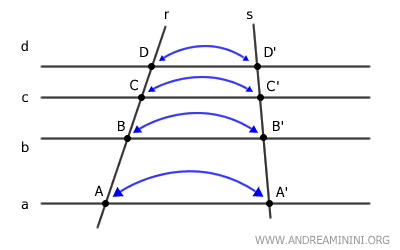
Esta correspondencia entre puntos implica una correspondencia única entre los segmentos de ambas transversales: AB corresponde a A'B', BC a B'C', etc.

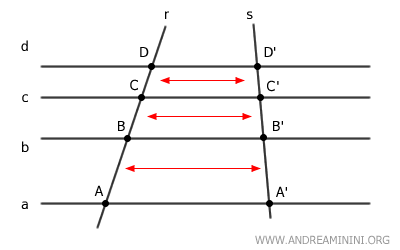
Nota: Esta correspondencia se fundamenta en que toda intersección de una transversal con una recta paralela tiene su homóloga sobre cualquier otra transversal que cruce las mismas rectas.

Para que se cumpla la proporcionalidad directa entre segmentos se deben verificar dos condiciones:

1. Por cada par de segmentos congruentes sobre r, existe un par congruente sobre s.
   
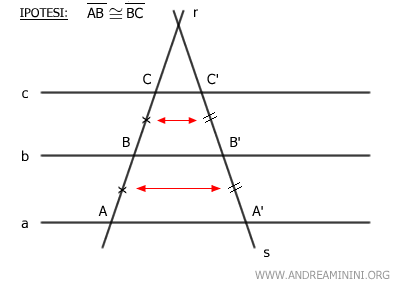
2. La suma de dos segmentos sobre r equivale a la suma de los correspondientes sobre s: AB + CD = A'B' + C'D'.
   

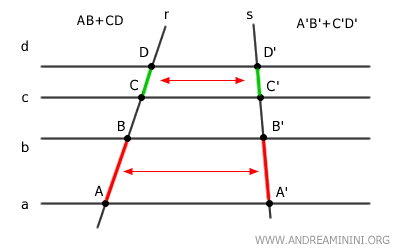
Ambas condiciones se cumplen como consecuencia de la correspondencia entre las rectas transversales.

Por lo tanto, los segmentos correspondientes sobre r y s son directamente proporcionales.

Observaciones

Algunas observaciones y corolarios relacionados con el teorema de Tales:

• Teorema de la recta paralela a un lado del triángulo
  Si una recta es paralela a un lado de un triángulo y corta a los otros dos, los divide en segmentos proporcionales, y viceversa. Es un corolario directo del teorema de Tales.

  Ejemplo: La recta r es paralela al lado AB y corta los lados AC y BC del triángulo.
  
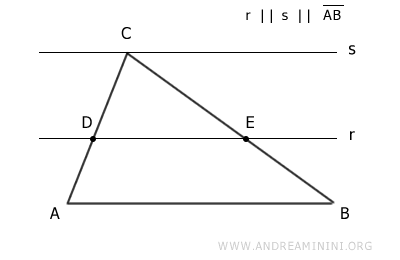
  Según Tales, se cumple la proporción: $$ \overline{AD} : \overline{DC} = \overline{BE} : \overline{EC} $$, lo que implica que los segmentos resultantes son directamente proporcionales.

• Teorema de la bisectriz
  La bisectriz de un ángulo interior de un triángulo divide el lado opuesto en dos segmentos proporcionales a los otros dos lados. $$ \overline{BD} : \overline{CD} = \overline{AB} : \overline{AC} $$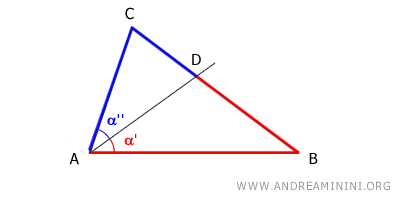

Y así sucesivamente.