Teorema de la bisectriz de un ángulo interior de un triángulo
La bisectriz de un ángulo interior de un triángulo divide el lado opuesto en dos segmentos que son proporcionales a los otros dos lados del triángulo. $$ \overline{BD} : \overline{CD} = \overline{AB} : \overline{AC} $$ 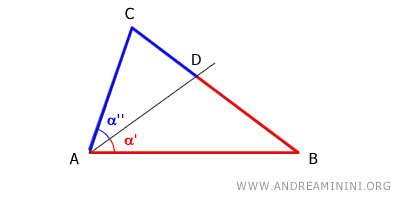
En otras palabras, si en un triángulo ABC se traza la bisectriz del ángulo en el vértice A y esta intersecta al lado opuesto BC en el punto D, entonces los segmentos BD y CD guardan entre sí la misma proporción que los lados AB y AC, respectivamente.
Expresado en forma matemática:
$$ \overline{AB} : \overline{AC} = \overline{BD} : \overline{CD} $$
o bien:
$$ \frac{\overline{AB}}{\overline{AC}} = \frac{\overline{BD}}{\overline{CD}} $$
Este teorema es especialmente útil en la resolución de problemas geométricos, ya que permite establecer relaciones métricas entre lados y segmentos de un triángulo cuando se conocen ciertas longitudes o ángulos.
También se cumple la recíproca: Si un punto divide un lado de un triángulo en dos segmentos proporcionales a los otros dos lados, entonces el segmento que une ese punto con el vértice opuesto es la bisectriz del ángulo correspondiente.
Ejemplo práctico
Consideremos un triángulo cuyos lados miden: AB = 4, BC = 5 y AC = 3.
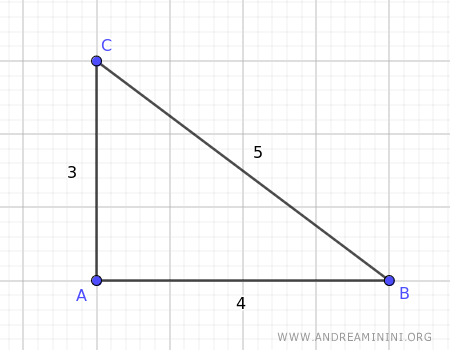
Se traza la bisectriz del ángulo en el vértice A.
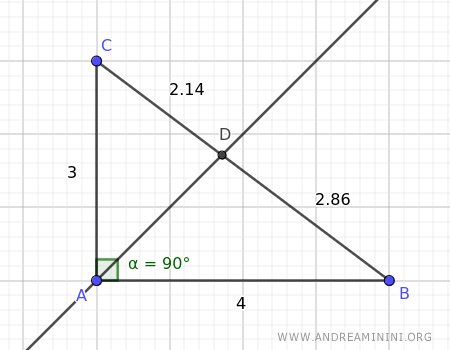
Esta bisectriz divide el lado opuesto BC en los segmentos BD = 2.86 y CD = 2.14.
La razón entre BD y CD es:
$$ \frac{\overline{BD}}{\overline{CD}} = \frac{2.86}{2.14} \approx 1.33 $$
Comparamos esta razón con la de los lados AB y AC:
$$ \frac{\overline{AB}}{\overline{AC}} = \frac{4}{3} \approx 1.33 $$
Como ambas razones coinciden, se concluye que los segmentos BD y CD son proporcionales a los lados AB y AC del triángulo.
Demostración
Sea ABC un triángulo cualquiera.
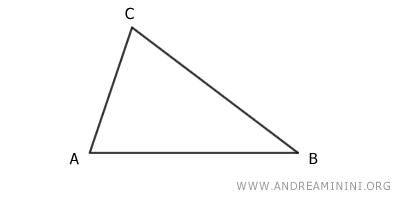
Se traza la bisectriz del ángulo $\hat{A}$, que corta al lado BC en el punto D, generando los segmentos BD y CD.
Dicha bisectriz divide el ángulo A en dos partes iguales: $\alpha' \cong \alpha''$.
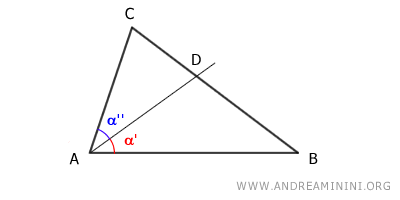
El objetivo es demostrar que:
$$ BD : CD = AB : AC $$
Es decir, que los segmentos BD y CD son proporcionales a los lados AB y AC.
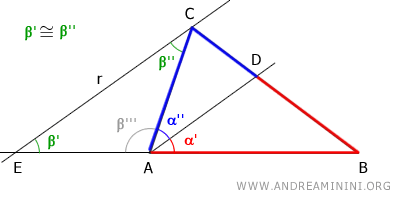
Para ello, trazamos por el vértice C una recta r paralela a la bisectriz AD.
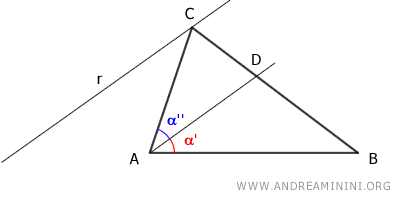
Prolongamos el lado BA hasta que corte a la recta r en un punto E.
Se forma así el triángulo EAC dentro del triángulo mayor EBC.
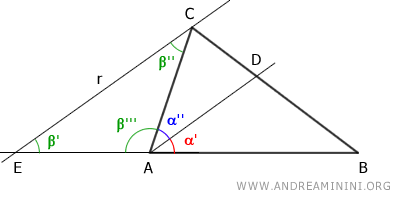
La recta AD, al ser paralela al lado EC del triángulo EBC, divide a los otros dos lados del triángulo en segmentos proporcionales, según el teorema de la recta paralela a un lado de un triángulo:
$$ BD : CD = AB : AE $$
Los ángulos $\alpha''$ y $\beta''$ son alternos internos respecto a las paralelas AD y EC cortadas por la transversal AC, y por tanto son congruentes:
$$ \alpha'' \cong \beta'' $$
De igual modo, los ángulos $\alpha'$ y $\beta'$ son correspondientes, y también son congruentes:
$$ \alpha' \cong \beta' $$
Como la bisectriz divide el ángulo A en dos ángulos iguales, se deduce que $\beta' \cong \beta''$, y por tanto el triángulo EAC es isósceles con base EC.
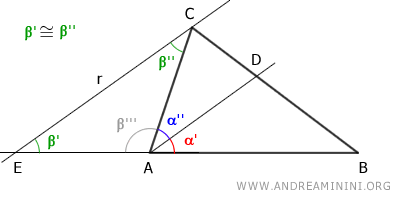
En consecuencia, los lados EA y AC son iguales:
$$ \overline{EA} \cong \overline{AC} $$
Volviendo a la proporción obtenida en el triángulo EBC:
$$ BD : CD = AB : AE $$
Y como $AE = AC$, se concluye:
$$ BD : CD = AB : AC $$
Lo que demuestra la afirmación inicial.
Por tanto, los segmentos BD y CD, generados al trazar la bisectriz del ángulo A, son proporcionales a los lados adyacentes AB y AC del triángulo.
Nota: Como el teorema de la recta paralela a un lado de un triángulo se deduce del teorema de Tales, el teorema de la bisectriz puede considerarse también un corolario de éste.
Y así sucesivamente.