Lado más largo y ángulo mayor en los triángulos
En cualquier triángulo no equilátero, el lado más largo se encuentra siempre frente al ángulo mayor, y viceversa.
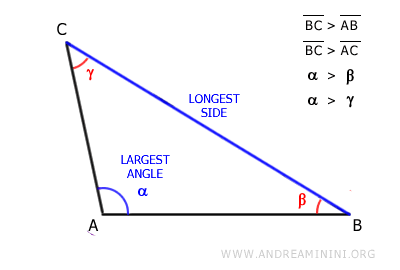
Este teorema se cumple en todos los triángulos, salvo en los equiláteros.
No aplica al triángulo equilátero, ya que en él los tres lados y los tres ángulos son iguales, por lo que no existe un lado más largo ni un ángulo mayor.
Un ejemplo práctico
Consideremos como ejemplo un triángulo escaleno y obtusángulo.
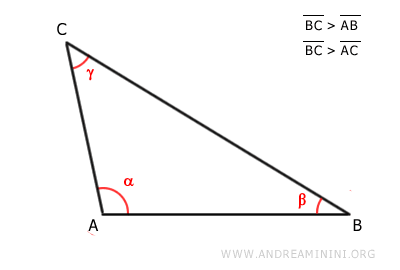
El ángulo más grande es el ángulo α en el vértice A.
$$ \alpha > \beta $$
$$ \alpha > \gamma $$
El lado opuesto al ángulo mayor α es el lado BC, que resulta ser el lado más largo del triángulo.
$$ \overline{BC} > \overline{AB} $$
$$ \overline{BC} > \overline{AC} $$
Y también se cumple el recíproco.
Demostración
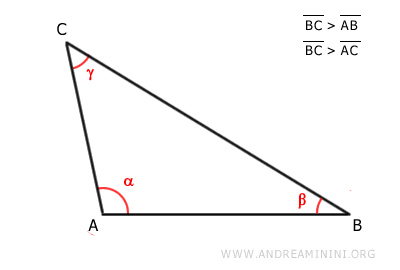
Partimos de la hipótesis de que el lado BC es el lado más largo del triángulo ABC.
$$ \overline{BC} > \overline{AC} $$
$$ \overline{BC} > \overline{AB} $$
Queremos demostrar que el ángulo opuesto al lado más largo BC, es decir, el ángulo α, es mayor que los otros dos ángulos.
Con centro en el vértice C y radio igual a CA, se traza un arco que corta al lado CB.
Llamamos a este punto de intersección punto D.
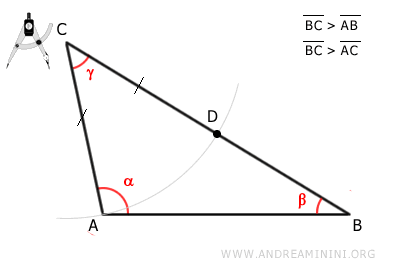
Por construcción, el segmento CD es congruente al segmento AC.
$$ \overline{CD} \cong \overline{AC} $$
Se traza el segmento AD.
Los puntos A, C y D forman un triángulo isósceles, ya que los lados AC y CD son congruentes.
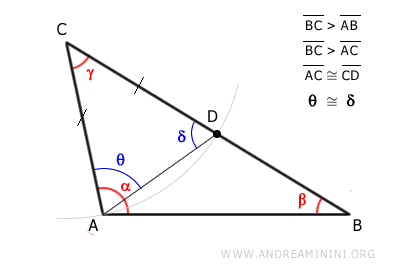
Al ser isósceles, el triángulo ACD posee dos ángulos iguales, δ y θ, adyacentes a la base AD.
$$ \delta \cong \theta $$
El ángulo δ es un ángulo exterior del triángulo ABD.
Según el teorema del ángulo exterior, el ángulo exterior δ es mayor que cualquiera de los ángulos internos no adyacentes β y α − θ del triángulo ABD.
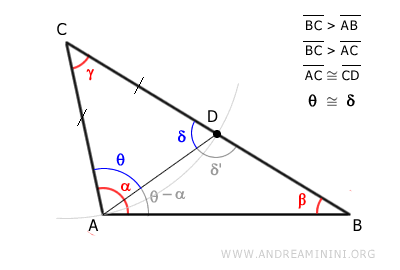
En particular, es importante destacar que el ángulo δ es mayor que β:
$$ \delta > \beta $$
Como los ángulos δ y θ son congruentes (δ ≅ θ), el ángulo θ también es mayor que β:
$$ \theta > \beta $$
Sin embargo, el ángulo θ es menor que el ángulo α (es decir, θ < α), ya que comparte uno de sus lados con α y su otro lado está contenido dentro del ángulo α.
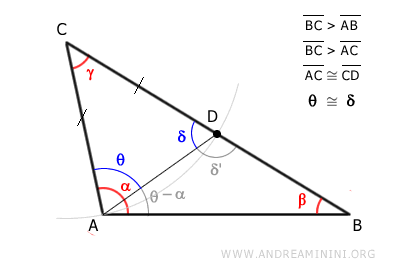
Por lo tanto, el ángulo α es mayor que el ángulo β:
$$ \alpha > \beta $$
Ahora debemos demostrar que el ángulo α también es mayor que el ángulo γ.
Volvemos al triángulo inicial ABC. Con centro en el punto B y radio igual a AB, se traza un arco que corta al lado AC.
Este arco determina el punto E.
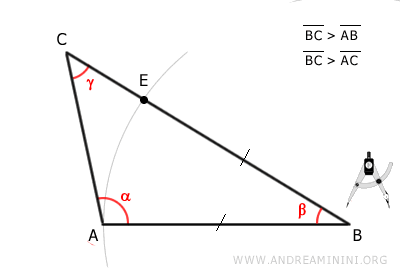
Así, el segmento EB es congruente al segmento AB.
$$ \overline{EB} \cong \overline{AB} $$
Se traza el segmento AE.
Los puntos A, B y E forman un triángulo isósceles, ya que los lados AB y EB son congruentes.
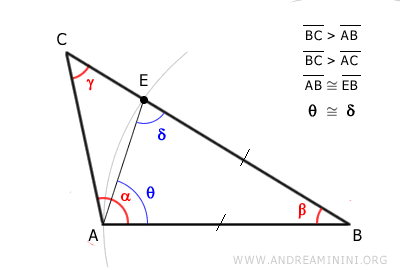
El triángulo ABE también posee dos ángulos iguales, δ y θ, adyacentes a la base AE.
$$ \delta \cong \theta $$
El ángulo δ es un ángulo exterior del triángulo ACE.
Por el teorema del ángulo exterior, el ángulo exterior δ es mayor que los ángulos internos no adyacentes γ y α − θ del triángulo ACE.
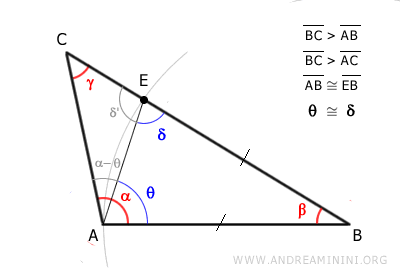
Es importante destacar que el ángulo δ es mayor que γ:
$$ \delta > \gamma $$
Como δ y θ son congruentes (δ ≅ θ), el ángulo θ también es mayor que γ:
$$ \theta > \gamma $$
El ángulo θ, sin embargo, es menor que el ángulo α (es decir, θ < α).
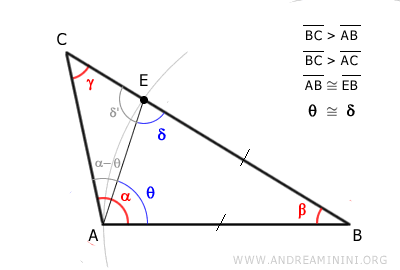
Por lo tanto, el ángulo α es mayor que el ángulo γ:
$$ \alpha > \gamma $$
En conclusión, el ángulo α, opuesto al lado más largo BC, es mayor que tanto el ángulo β como el ángulo γ.
Por lo tanto, el ángulo α es el mayor ángulo del triángulo ABC.
Observaciones
A continuación, algunas observaciones y corolarios derivados de este teorema:
- En un triángulo rectángulo, la hipotenusa es siempre el lado más largo en comparación con los catetos.
- En un triángulo obtusángulo, el lado opuesto al ángulo obtuso es siempre el más largo respecto a los otros dos lados.
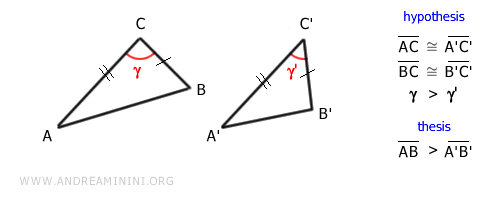
- Corolario
Si dos triángulos tienen dos lados congruentes en el mismo orden (por ejemplo, AC ≅ A'C' y BC ≅ B'C'), pero distintos ángulos comprendidos, el que tenga el ángulo mayor (por ejemplo, γ > γ') también tendrá el lado opuesto más largo (es decir, AB > A'B').
Y así sucesivamente.