Triángulo isósceles

Un triángulo isósceles es una figura triangular que presenta dos lados de igual longitud, conocidos como lados iguales o lados isósceles.

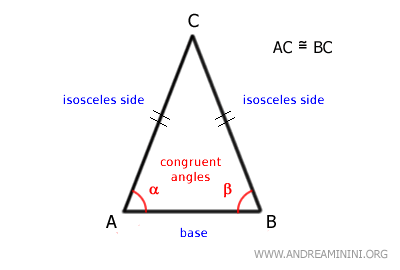
El tercer lado se denomina base del triángulo.

Los lados iguales forman dos ángulos en la base, que también son iguales entre sí.

El ángulo opuesto a la base recibe el nombre de ángulo del vértice.

¿Por qué se llama isósceles? La palabra “isósceles” proviene del griego antiguo: “isos” significa “igual” y “skelos” quiere decir “pierna” o “lado”. Por tanto, isósceles significa literalmente “lados iguales”, una descripción perfecta de este tipo de triángulo.

Un ejemplo práctico

Observa el triángulo ABC.

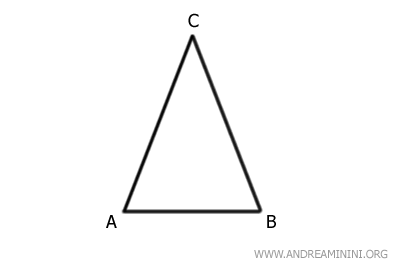
Los lados AC y BC son congruentes, es decir, tienen la misma longitud.

Estos constituyen los lados iguales o lados isósceles del triángulo.

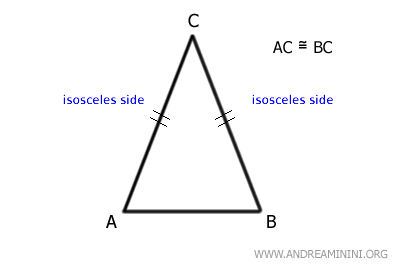
El lado restante, AB, que no es congruente con los otros dos, se considera la base.

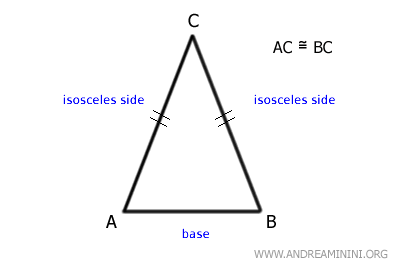
Los lados isósceles determinan dos ángulos iguales, ubicados junto a la base.

Estos se conocen como los ángulos de la base.

Al triángulo isósceles ABC también se le puede llamar “triángulo isósceles con vértice en C”.

Observaciones

Estas son algunas propiedades importantes de los triángulos isósceles:

• Un triángulo isósceles tiene dos lados congruentes (AC≅BC)
  

  

• Teorema del triángulo isósceles

  Un triángulo es isósceles si, y solo si, posee dos ángulos iguales (α≅β).

  Esto se debe a que, en cualquier triángulo, los lados opuestos a ángulos iguales también son iguales.
  

  Nota. Dicho de forma simple: si un triángulo tiene dos ángulos iguales, entonces es isósceles. Y al revés: todo triángulo isósceles presenta siempre dos ángulos iguales.

• Los ángulos de la base de un triángulo isósceles siempre son agudos
  
  Esto ocurre porque, al ser iguales, no pueden ser rectos ni obtusos. En un triángulo, no pueden existir dos ángulos rectos u obtusos al mismo tiempo.
  

  Explicación. Si ambos ángulos de la base fueran rectos u obtusos, se contradiría el teorema sobre la suma de los ángulos interiores, que afirma que en todo triángulo debe haber al menos dos ángulos agudos. Por tanto, un triángulo no puede tener más de un ángulo que no sea agudo.

• La bisectriz en un triángulo isósceles

  En un triángulo isósceles, la bisectriz del ángulo opuesto a la base coincide con la mediana, la altura y la mediatriz de la base.

  
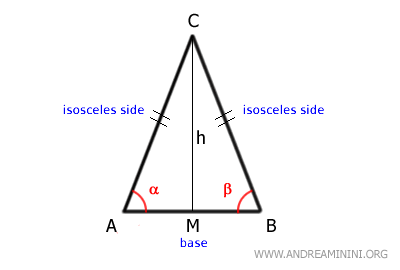
  Esta altura (h), trazada desde el vértice hasta la base, genera dos triángulos rectángulos congruentes (AMC≅BCM) y divide la base en dos segmentos iguales (AM≅BM).
• Un triángulo equilátero es un caso particular de triángulo isósceles en el que los tres lados son iguales. Por tanto, todo triángulo equilátero es isósceles, pero no todo triángulo isósceles es equilátero. En el equilátero, cualquier lado puede considerarse base, y sus tres ángulos miden 60°.
  
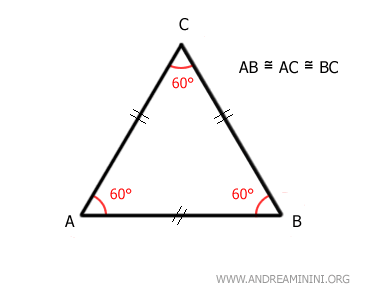
• La suma de los ángulos interiores de cualquier triángulo, incluido el isósceles, es siempre de 180 grados.
• Un triángulo isósceles puede ser acutángulo, rectángulo u obtusángulo.
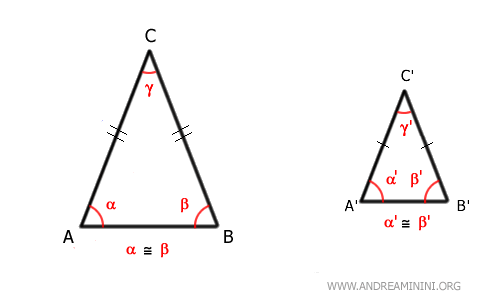
• Dos triángulos isósceles son semejantes si comparten el mismo ángulo del vértice
  Dos triángulos isósceles son semejantes si tienen el mismo ángulo del vértice, es decir, el ángulo comprendido entre los lados iguales. Esto se debe a que la suma de los ángulos interiores en cualquier triángulo es 180 grados. Si los ángulos del vértice γ≅γ' son iguales, los ángulos de la base en ambos triángulos serán iguales a (180° - γ) ÷ 2. Por tanto, los tres ángulos de ambos triángulos son congruentes y, según el primer criterio de semejanza de triángulos, son semejantes: tienen la misma forma, aunque no necesariamente el mismo tamaño.
  

Y así sucesivamente.