Primer Teorema de Euclides
En un triángulo rectángulo, el área del cuadrado construido sobre uno de sus catetos es igual al área del rectángulo que se obtiene al proyectar dicho cateto sobre la hipotenusa, tomando como altura la longitud de la hipotenusa.
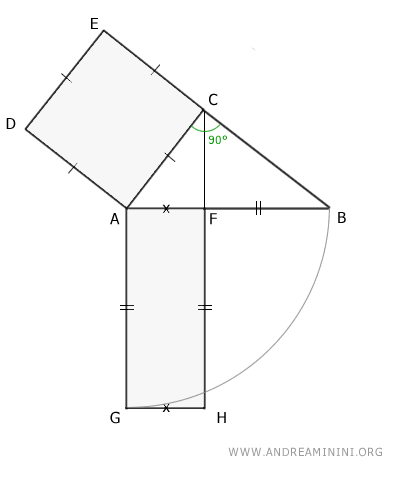
Dicho de otro modo, si proyectamos los catetos AC o BC de un triángulo rectángulo sobre la hipotenusa AB, se generan dos segmentos, AF y BF, tales que:
$$ \overline{AF} + \overline{BF} = \overline{AB} $$
El teorema de Euclides establece que el área del cuadrado construido sobre el cateto AC, es decir AC2, coincide con el área del rectángulo cuyos lados miden AB y AF.
$$ \overline{AC}^2 = \overline{AB} \cdot \overline{AF} $$
Y de manera análoga, se cumple lo mismo para el otro cateto.
Nota. El primer teorema de Euclides describe las relaciones proporcionales entre los lados de un triángulo rectángulo, las proyecciones de sus catetos sobre la hipotenusa y la propia hipotenusa. Esto lo diferencia del Teorema de Pitágoras, que expresa una igualdad entre áreas: la suma de las áreas de los cuadrados construidos sobre los catetos equivale al área del cuadrado construido sobre la hipotenusa.
Como corolario, puede afirmarse también que, en un triángulo rectángulo, cada cateto es media proporcional entre la hipotenusa y su proyección sobre ella.
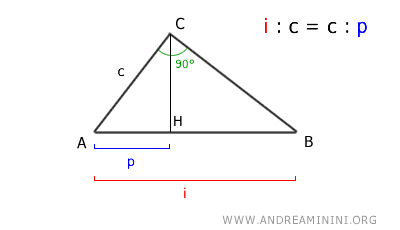
Es decir, la hipotenusa (i) guarda la misma proporción con el cateto (c) que ese cateto (c) con su proyección (p) sobre la hipotenusa.
Nota. La proporción i:c = c:p es completamente equivalente al primer teorema de Euclides: $$ i : c = c : p \rightarrow c^2 = i \cdot p $$ Se trata simplemente de dos formas distintas de expresar el mismo principio.
Un Ejemplo Práctico
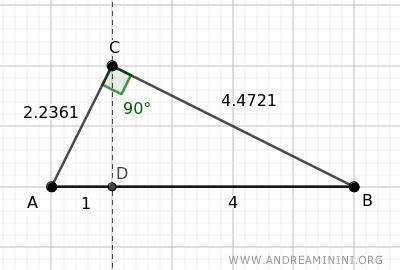
Consideremos un triángulo rectángulo con las siguientes medidas: AB=5, BC=4.4721 y AC=2.2361.
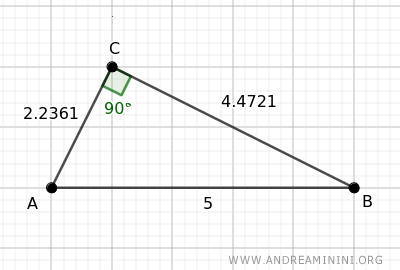
Proyectamos el cateto AC sobre la hipotenusa AB.
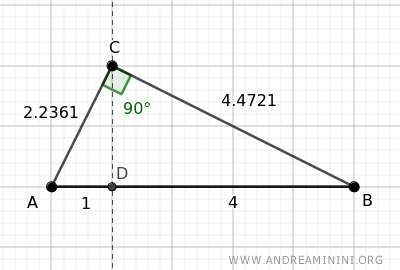
La proyección divide la hipotenusa AB=5 en dos segmentos: AD=1 y BD=4.
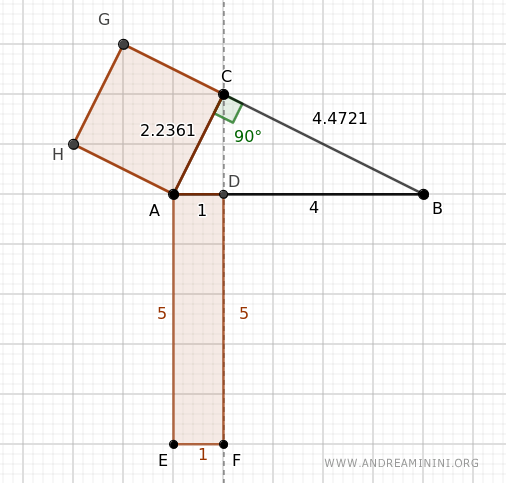
Calculamos ahora el área del cuadrado construido sobre el cateto AC:
$$ \overline{AC}^2 = 2.2361^2 = 5 $$
A continuación, hallamos el área del rectángulo formado por la proyección del cateto AC sobre la hipotenusa, que es AD=1, y cuyo otro lado mide lo mismo que la hipotenusa AB=5.
$$ \overline{AD} \cdot \overline{AB} = 1 \cdot 5 = 5 $$
Como podemos ver, ambas áreas coinciden perfectamente, tal y como predice el teorema de Euclides.
Ejemplo 2
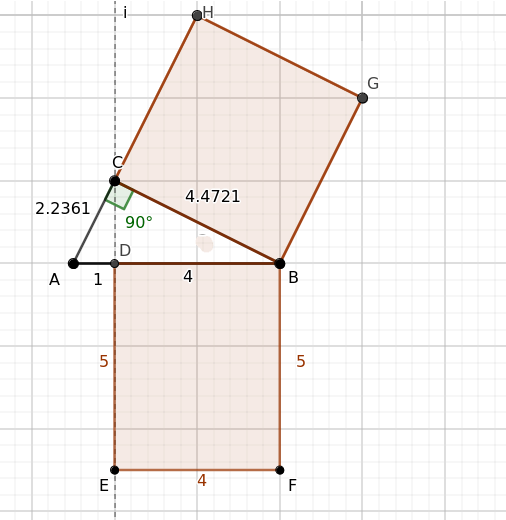
Para completar el ejercicio, calculemos ahora el cuadrado construido sobre el otro cateto, BC.
En este caso, el cuadrado sobre el lado BC=4.4721 tiene un área de:
$$ \overline{BC}^2 = 4.4721^2 = 20 $$
Después, calculamos el área del rectángulo cuya base es la proyección del cateto BC sobre la hipotenusa, que es BD=4, y cuya altura mide lo mismo que la hipotenusa AB=5.
$$ \overline{BD} \cdot \overline{AB} = 4 \cdot 5 = 20 $$
Nuevamente, el resultado confirma exactamente lo establecido por el teorema.
La Demostración
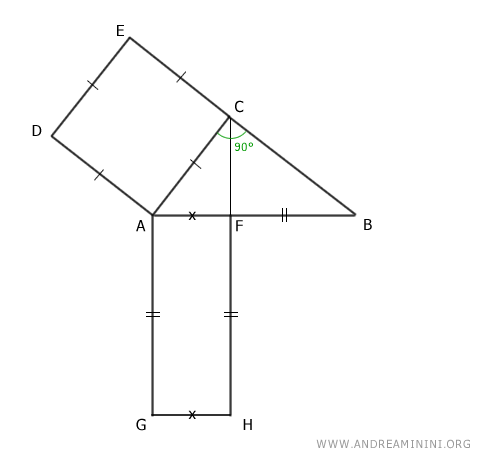
Consideremos el triángulo rectángulo ABC.
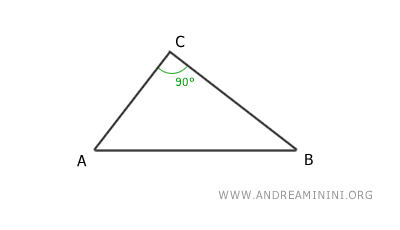
Construyamos sobre el cateto AC el cuadrado ACED.
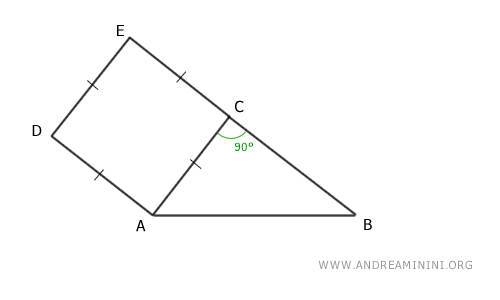
Proyectamos el cateto AC sobre la hipotenusa AB, dividiéndola en dos segmentos, AF y BF.
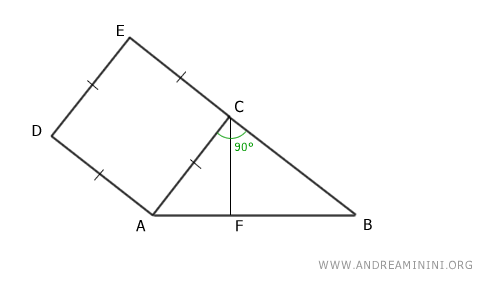
Construimos un rectángulo cuya base sea la proyección del cateto sobre la hipotenusa y cuya altura coincide con la hipotenusa.
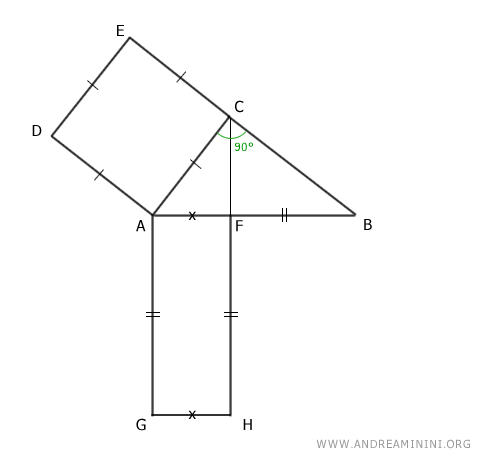
Así, este rectángulo posee lados congruentes a la hipotenusa.
$$ \overline{AF} \cong \overline{AG} \cong \overline{FH} $$
Se trazan rectas que prolongan los lados del rectángulo y la recta opuesta del cuadrado respecto al cateto.
Se designan los puntos de intersección como K y L.
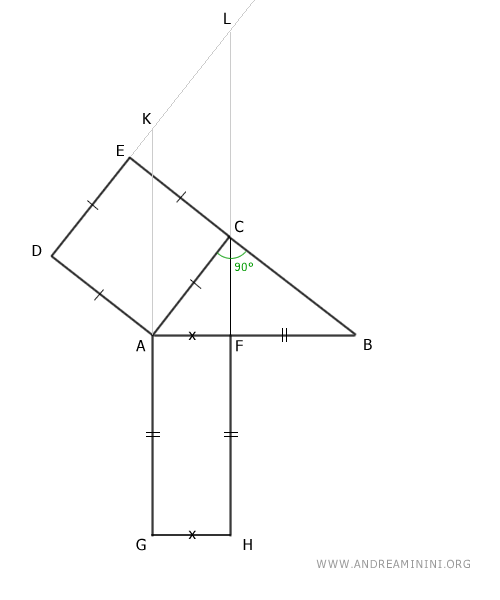
Observamos ahora los ángulos formados en el cuadrado sobre el cateto AC y su relación con la hipotenusa.
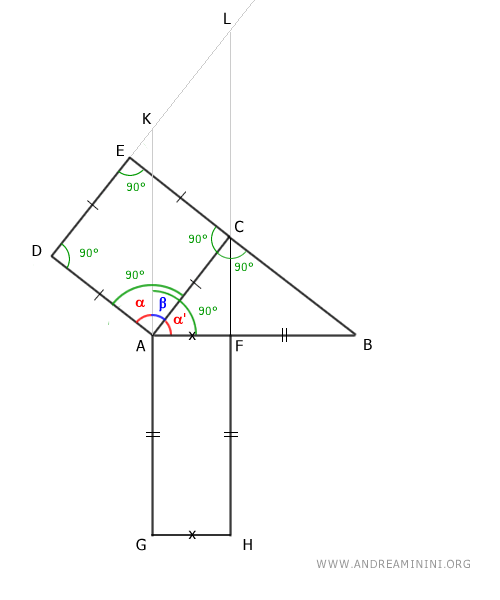
Los ángulos α y α' son congruentes (α≅α') porque ambos son complementarios del ángulo β, dado que tanto el cuadrado como el rectángulo tienen ángulos rectos (90°).
$$ \alpha + \beta = 90° $$
$$ \alpha ' + \beta = 90° $$
Por lo tanto, se concluye que son congruentes:
$$ \alpha + \beta = \alpha ' + \beta $$
$$ \alpha = \alpha ' $$
Los triángulos AKD y ABC son congruentes según el segundo criterio de congruencia de triángulos, ya que comparten un lado congruente AC≅AD y presentan ángulos adyacentes iguales: uno recto de 90° y otro α≅α'.
$$ AKD \cong ABC $$
Al ser congruentes, los triángulos AKD y ABC poseen todos sus lados y ángulos correspondientes iguales.
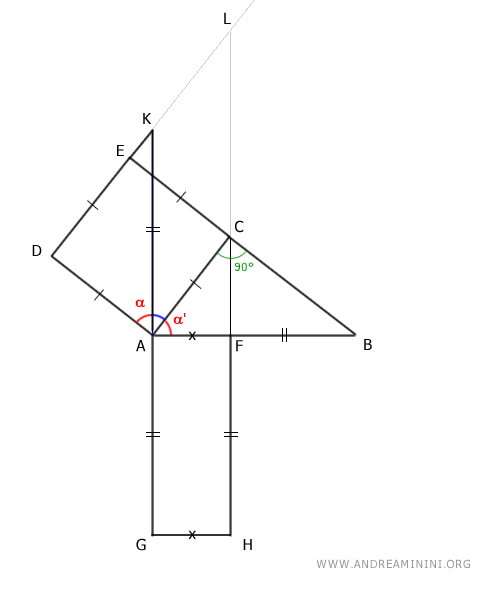
Un detalle relevante es que los lados AK y AB resultan congruentes.
$$ \overline{AK} \cong \overline{AB} $$
Por construcción, el cuadrilátero ACLK es un paralelogramo, ya que presenta lados opuestos paralelos.
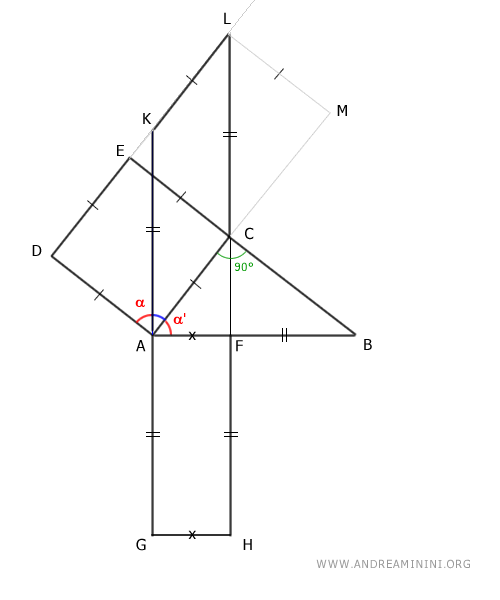
Según el principio de equivalencia de paralelogramos, el cuadrado ACED y el paralelogramo ACLK son equivalentes en área, pues comparten la misma base AC y poseen alturas congruentes EA≅LM.
$$ ACED \doteq ACLK $$
De igual forma, el rectángulo AFHG y el paralelogramo ACLK son equivalentes, ya que tienen bases congruentes AG≅AK y comparten la misma altura AH.
$$ AFHG \doteq ACLK $$
Por la propiedad transitiva, se deduce que el cuadrado ACED y el rectángulo AFHG son equivalentes en área.
$$ ACED \doteq ACLK \doteq AFHG $$
$$ ACED \doteq AFHG $$
Así queda demostrado que el área del cuadrado construido sobre el cateto AC es igual al área del rectángulo construido sobre su proyección en la hipotenusa, siendo esta última uno de sus lados.
Esto prueba el primer teorema de Euclides para triángulos rectángulos.
Nota. Del mismo modo, esta propiedad puede demostrarse para el otro cateto BC del triángulo rectángulo.
Corolario
En un triángulo rectángulo, cada cateto (c) es media proporcional entre la hipotenusa (i) y su proyección (p) sobre ella.
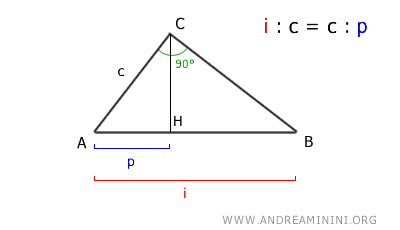
Es decir, la hipotenusa se relaciona con el cateto del mismo modo que el cateto con su proyección sobre la hipotenusa.
$$ i:c = c:p $$
En términos algebraicos, esto implica que el cuadrado del cateto (c) es igual al producto de la hipotenusa (i) por la proyección (p) del cateto sobre la hipotenusa.
$$ \frac{i}{c} = \frac{c}{p} $$
$$ c^2 = i \cdot p $$
Esto nos conduce nuevamente al primer teorema de Euclides, el cual establece que el área del cuadrado construido sobre un cateto en un triángulo rectángulo equivale al área del rectángulo formado por su proyección sobre la hipotenusa y la propia hipotenusa.
Ejemplo
Retomemos el ejemplo anterior del triángulo rectángulo ABC, cuyas dimensiones ya conocemos.
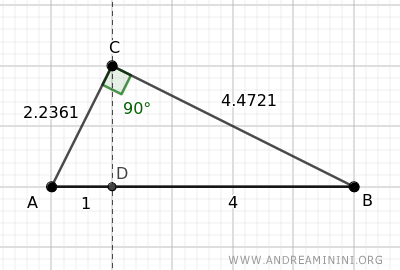
El cateto AC mide aproximadamente 2.2361, su proyección sobre la hipotenusa (AD) mide 1, y la hipotenusa AB mide 5.
Según el corolario, el cateto AC es media proporcional entre la hipotenusa AB y su proyección AD sobre la hipotenusa.
$$ \overline{AB} : \overline{AC} = \overline{AC} : \overline{AD} $$
Si sustituimos los valores conocidos:
$$ 5 : 2.2361 = 2.2361 : 1 $$
En esta proporción, la longitud del cateto (2.2361) actúa efectivamente como media proporcional.
La igualdad se verifica, aunque con ligeras diferencias debidas a redondeos en las cifras decimales obtenidas mediante GeoGebra.
$$ 2.2361 = 2.2361 $$
La misma relación es válida para el otro cateto BC del triángulo rectángulo.
Aunque pueda haber mínimas diferencias por redondeo en los cálculos de GeoGebra, este ejemplo ilustra la validez del corolario con valores concretos.
Demostración
Consideremos el triángulo rectángulo ABC y el cateto AC.
El segmento AH corresponde a la proyección del cateto AC sobre la hipotenusa AB.
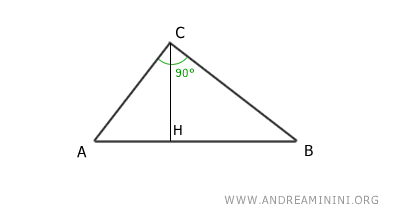
De acuerdo con el primer criterio de semejanza de triángulos, los triángulos ABC y AHC son semejantes, pues tienen dos ángulos congruentes en el mismo orden: uno recto (90°) y uno coincidente (α).
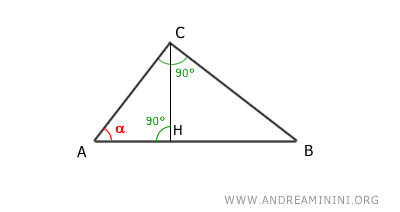
Nota. Si dos triángulos comparten dos ángulos iguales, el tercero también lo es, ya que la suma de los ángulos interiores siempre es 180°.
Por lo tanto, los triángulos ABC y AHC son semejantes.
$$ ABC \approx AHC $$
Y siendo semejantes, sus lados correspondientes guardan proporción.
$$ \overline{AB} : \overline{AC} = \overline{AC} : \overline{AH} = \overline{CB} : \overline{CH} $$
Esto demuestra el corolario: la hipotenusa (AB) está en la misma proporción con el cateto (AC) que este con su proyección (AH) sobre la hipotenusa.
$$ \overline{AB} : \overline{AC} = \overline{AC} : \overline{AH} $$
Y así sucesivamente.