Suma de los ángulos interiores de un triángulo
La suma de los ángulos interiores de un triángulo es siempre igual a un ángulo llano (180°).
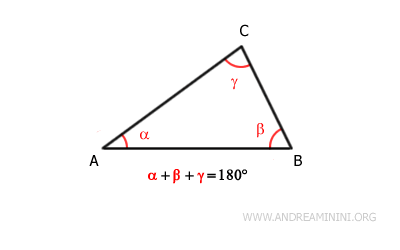
En consecuencia, la suma de los ángulos interiores de cualquier triángulo es:
$$ \alpha + \beta + \gamma = 180° $$
Demostración
Consideremos un triángulo cualquiera ABC.
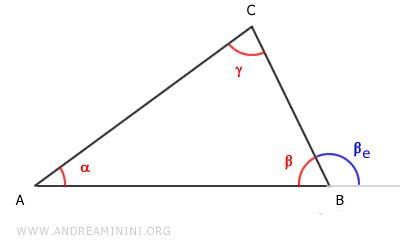
El ángulo exterior $ \beta_e $ es suplementario de $ \beta $, pues ambos suman un ángulo llano:
$$ \beta + \beta_e = 180° $$
De acuerdo con el teorema del ángulo exterior, dicho ángulo exterior es igual a la suma de los dos ángulos interiores no adyacentes:
$$ \beta_e \cong \alpha + \gamma $$
Combinando ambas relaciones:
$$ \beta + (\alpha + \gamma) = 180° $$
De donde se deduce:
$$ \alpha + \beta + \gamma = 180° $$
Queda así demostrada la propiedad: la suma de los ángulos interiores de cualquier triángulo es 180°.
Demostración alternativa
Consideremos nuevamente el triángulo ABC.
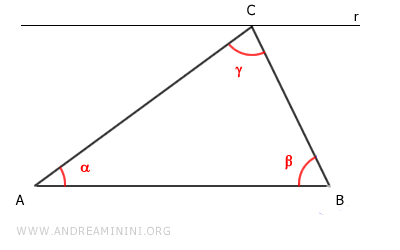
Se traza una recta paralela al lado AB que pasa por el vértice C del triángulo.
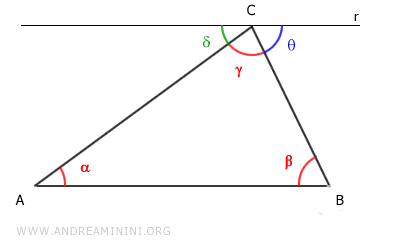
Los ángulos $ \delta + \gamma + \theta $ suman un ángulo llano:
$$ \delta + \gamma + \theta = 180° $$
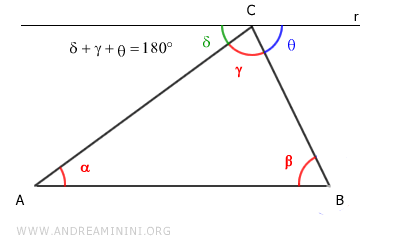
Por el teorema de las paralelas, los ángulos alternos internos son congruentes:
- $ \alpha \cong \delta $, con respecto a la transversal AC.
- $ \beta \cong \theta $, con respecto a la transversal BC.
Por tanto:
$$ \alpha + \beta + \gamma = \delta + \theta + \gamma = 180° $$
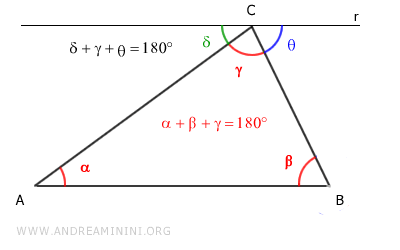
En conclusión, la suma de los ángulos interiores de un triángulo es siempre igual a 180°.
Y así sucesivamente.