Triángulo rectángulo con ángulos de 45°
Un triángulo rectángulo con ángulos agudos de 45° presenta dos lados iguales (los catetos), ya que se trata, además, de un triángulo isósceles.
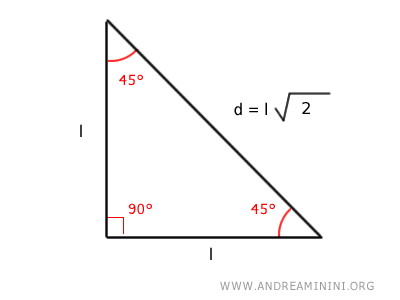
En este tipo de triángulo, la hipotenusa, opuesta al ángulo recto, se determina mediante la fórmula $$ d = l \cdot \sqrt{2} $$ Los lados que forman el ángulo recto son congruentes.
Explicación
Este caso particular de triángulo rectángulo se conoce también como "triángulo rectángulo isósceles".
Los dos ángulos agudos que flanquean la hipotenusa (a) son iguales, midiendo 45° cada uno. Esto convierte al triángulo en un triángulo isósceles.
En consecuencia, sus dos catetos son iguales b ≅ c, es decir, poseen la misma longitud, lo que confiere simetría al triángulo respecto de la hipotenusa.
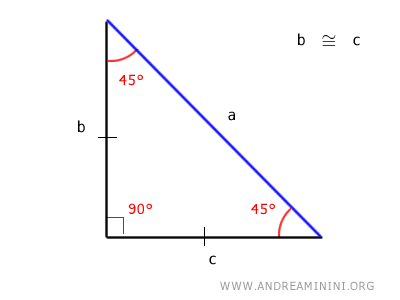
De hecho, si se duplica este triángulo, se obtiene un cuadrado perfecto.
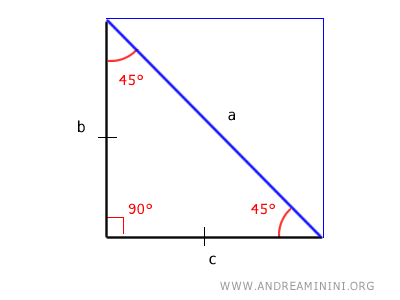
Gracias a esta propiedad tan característica, es posible calcular la longitud de todos sus lados conociendo únicamente uno de ellos.
$$ c = \frac{a}{ \sqrt{2} } = \frac{a}{2} \sqrt{2} $$
$$ a = c \cdot \sqrt{2} $$
Conviene recalcar que estas fórmulas son válidas exclusivamente para triángulos con dos ángulos de 45°.
Otra propiedad notable del triángulo rectángulo isósceles es que, si se traza una altura desde la hipotenusa hasta el vértice opuesto (el ángulo recto), dicha altura divide la hipotenusa en dos segmentos iguales y origina dos triángulos rectángulos más pequeños, ambos con ángulos de 45°.
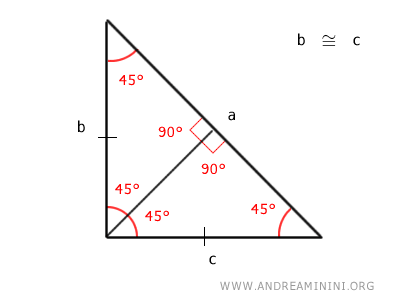
Demostración
Consideremos un triángulo rectángulo cuyos ángulos agudos midan 45°.
Los ángulos contiguos al lado "a" son congruentes, lo que hace que el triángulo rectángulo sea, a su vez, un triángulo isósceles, es decir, con dos lados iguales.
Si sabemos que el lado "a" actúa como base del triángulo isósceles, entonces los otros dos lados deben ser congruentes.
$$ b \cong c $$
Dado que b = c, podemos representar ambos catetos con una sola letra, por ejemplo, "c."
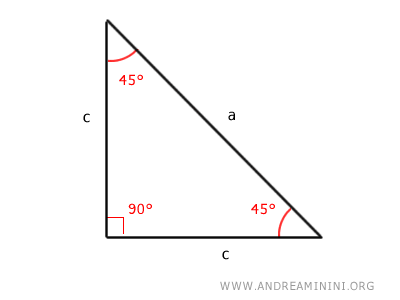
De acuerdo con el teorema de Pitágoras, en un triángulo rectángulo, el cuadrado de la hipotenusa (a2) es igual a la suma de los cuadrados de los catetos (c2 + c2).
$$ a^2 = c^2 + c^2 $$
$$ a^2 = 2c^2 $$
Esta relación permite calcular la longitud de la hipotenusa (a) si se conoce la longitud de uno de los catetos (c).
$$ a^2 = 2c^2 $$
$$ \sqrt{a^2} = \sqrt{2c^2} $$
$$ a = c \cdot \sqrt{2} $$
Si, en cambio, conocemos la longitud de la hipotenusa (a), podemos determinar la longitud de los catetos (c).
$$ a^2 = 2c^2 $$
$$ \frac{a^2}{2} = c^2 $$
$$ \sqrt{\frac{a^2}{2}} = \sqrt{c^2} $$
$$ a \cdot \frac{1}{\sqrt{2}} = c $$
$$ c = \frac{a}{\sqrt{2}} $$
Aplicando la propiedad invariativa de las fracciones, multiplicamos numerador y denominador por la raíz cuadrada de 2.
$$ c = \frac{a \cdot \sqrt{2}}{\sqrt{2} \cdot \sqrt{2}} $$
$$ c = \frac{a}{2} \sqrt{2} $$
Y así sucesivamente.