Relación entre los lados y los ángulos opuestos en un triángulo

En cualquier triángulo existe una relación esencial entre la longitud de sus lados y la medida de los ángulos opuestos.

• Si dos lados de un triángulo son congruentes, entonces los ángulos opuestos a esos lados también lo son. Por ejemplo, en un triángulo isósceles, los dos lados iguales corresponden a dos ángulos opuestos de igual medida.
  
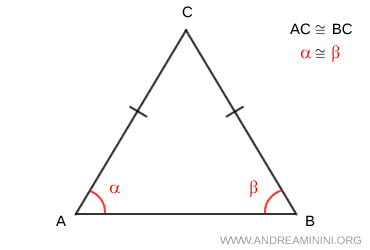
• Si un triángulo tiene dos lados de distinta longitud, los ángulos opuestos también son desiguales: el lado más largo siempre está frente al ángulo de mayor medida.
  

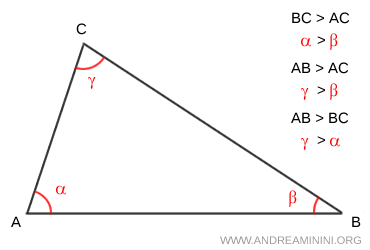
Demostración

Supongamos que tenemos un triángulo en el cual uno de sus lados es mayor que otro.

$$ BC > AC $$

Queremos demostrar que el ángulo $ \alpha $, opuesto al lado $ BC $, es mayor que el ángulo $ \beta $, opuesto al lado $ AC $.

Como $ BC $ es mayor que $ AC $, existe necesariamente un punto $ P $ sobre el segmento $ BC $ tal que $ AB \cong CP $.

Por construcción, el triángulo $ \triangle ACP $ es isósceles, pues posee dos lados congruentes: $ AB \cong CP $. Esto implica que sus ángulos en la base, a los que llamaremos $ \theta $, son iguales.

Como el segmento $ AP $ divide al ángulo $ \alpha $, se deduce que $ \alpha $ es mayor que $ \theta $.

$$ \alpha > \theta $$

Ahora, si consideramos el triángulo $ \triangle APC $, vemos que $ \theta $ es también un ángulo exterior.

Según el teorema del ángulo exterior, en cualquier triángulo un ángulo exterior es mayor que cualquiera de los ángulos interiores no adyacentes.

Por lo tanto, se concluye que $ \theta $ es mayor que $ \beta $.

$$ \theta > \beta $$

En resumen, se establece la siguiente relación de desigualdad:

$$ \alpha > \theta > \beta $$

Siendo $ \alpha $ el ángulo opuesto al lado más largo $ BC $, y $ \beta $ el ángulo opuesto al lado más corto $ AC $.

Hemos demostrado, así, que en cualquier triángulo, el lado más largo está siempre frente al ángulo de mayor medida.

Teorema recíproco

En un triángulo, si dos ángulos no son congruentes, entonces el lado opuesto al ángulo mayor es necesariamente más largo que el lado opuesto al ángulo menor.

De este principio se derivan importantes conclusiones:

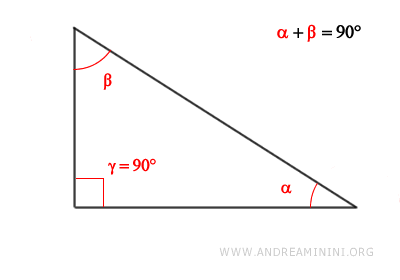
• En un triángulo rectángulo, la hipotenusa es siempre el lado más largo, ya que se encuentra opuesta al ángulo recto (90°), que es el ángulo de mayor medida en el triángulo.
  
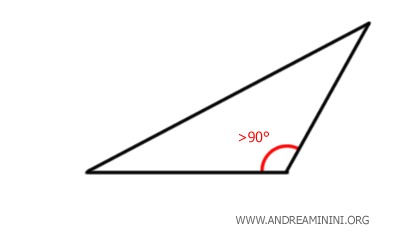
• En un triángulo obtusángulo, el lado opuesto al ángulo obtuso (mayor de 90°) es siempre más largo que cualquiera de los otros dos lados.
  

Y esta relación se cumple en todos los casos.