Criterios de congruencia de triángulos
Los tres criterios de congruencia de triángulos permiten determinar si dos triángulos son congruentes a partir de ciertos datos específicos.
En general, según la definición de congruencia, dos figuras geométricas son congruentes si pueden superponerse exactamente mediante un movimiento rígido.
Esta regla también se aplica a los triángulos, aunque en su forma más estricta exige conocer todos los elementos de la figura.
No obstante, existen tres criterios fundamentales de congruencia que permiten establecer la congruencia de dos triángulos con solo tres elementos concretos.
¿Por qué utilizar los criterios de congruencia? Estos criterios comparan lados y ángulos, evitando la necesidad de contrastar todos los pares de puntos de las figuras. Así, el procedimiento es mucho más eficiente y puede basarse en información parcial.
Primer criterio de congruencia de triángulos
Dos triángulos son congruentes si tienen dos lados y el ángulo comprendido entre ellos congruentes y dispuestos en el mismo orden.
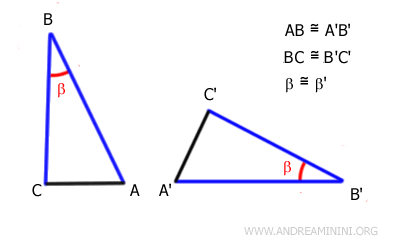
En la práctica, dos triángulos son congruentes si poseen dos lados de la misma longitud y el ángulo comprendido entre ellos es igual.
Este criterio también se conoce como criterio Lado-Ángulo-Lado (LAL) o SAS (Side-Angle-Side).
Conviene señalar que el ángulo debe ser necesariamente el comprendido entre los dos lados: si no lo es, los triángulos podrían no ser congruentes.
Por ejemplo, considera el triángulo ABC. Se traza una circunferencia de radio AC con centro en A. El arco corta la prolongación del segmento AC en el punto D, definiendo así un nuevo triángulo ACD.
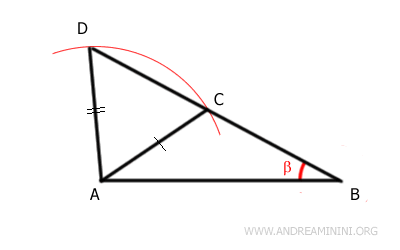
Los triángulos ABC y ABD no son congruentes. Aunque comparten dos lados congruentes AB ≅ AB y AC ≅ AD, y el ángulo β también es congruente, este ángulo no es el comprendido entre los dos lados. Por tanto, disponer de dos lados y un ángulo que no sea el comprendido entre ellos no garantiza la congruencia.
El primer criterio de congruencia se considera un postulado.
Segundo criterio de congruencia de triángulos
Dos triángulos son congruentes si tienen dos ángulos y el lado comprendido entre ellos congruentes y dispuestos en el mismo orden.
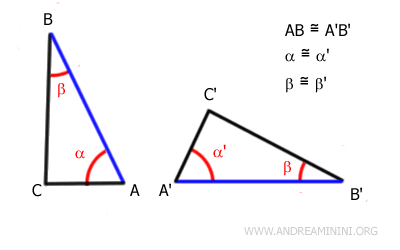
En otras palabras, dos triángulos son congruentes si presentan dos ángulos de igual medida y el lado comprendido entre dichos ángulos es congruente.
Este criterio también se conoce como criterio Ángulo-Lado-Ángulo (ALA) o ASA (Angle-Side-Angle).
A diferencia del primero, este criterio es un teorema, ya que puede demostrarse.
Según el quinto postulado de Euclides, la suma de los ángulos interiores de un triángulo siempre es igual a un ángulo llano (180°). Por tanto, si se conocen dos ángulos, se puede determinar el tercero por simple resta.
Este criterio también admite una variante más general, conocida como segundo criterio generalizado o cuarto criterio de congruencia de triángulos.
Dos triángulos son congruentes si tienen dos ángulos y un lado congruente en el mismo orden, aunque dicho lado no sea necesariamente el comprendido entre los dos ángulos.
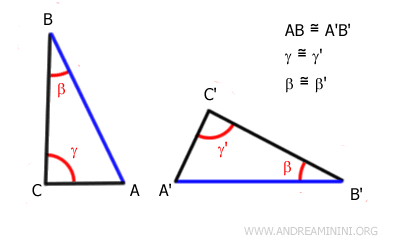
En este caso, el lado congruente puede ser cualquiera de los tres lados del triángulo.
Tercer criterio de congruencia de triángulos
Dos triángulos son congruentes si tienen los tres lados congruentes.
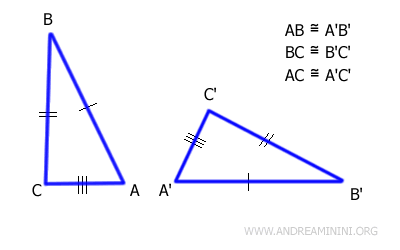
En la práctica, dos triángulos son congruentes si todos sus lados tienen la misma longitud.
Este criterio también se conoce como criterio Lado-Lado-Lado (LLL) o SSS (Side-Side-Side).
Como el anterior, es un teorema y puede ser demostrado rigurosamente.
Nota: La congruencia de ángulos (AAA) es una condición necesaria pero no suficiente para la congruencia de triángulos. Dos triángulos pueden tener ángulos iguales pero lados de longitudes diferentes. En tal caso, no son congruentes, ya que no pueden superponerse exactamente: tendrán la misma forma, pero distinta escala. En cambio, dos triángulos con lados congruentes (LLL) siempre tendrán ángulos congruentes. Por tanto, el criterio AAA no constituye un criterio válido de congruencia.
Y así sucesivamente.