Incentro de un Triángulo
El incentro de un triángulo es el punto donde se intersectan las bisectrices de sus ángulos interiores, y constituye el centro de la circunferencia inscrita en el triángulo (también llamada circunferencia inscrita).
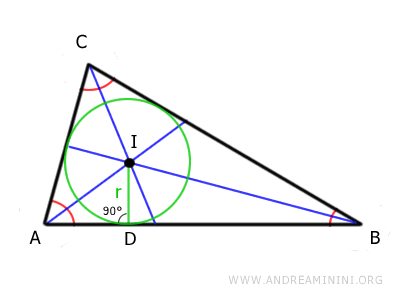
La propiedad principal del incentro (I) es que se encuentra a la misma distancia de los tres lados del triángulo.
Dicha distancia (ID) corresponde al radio de la circunferencia inscrita en el triángulo, conocida como la circunferencia inscrita.
La circunferencia inscrita es tangente a los tres lados del triángulo, es decir, los toca en un único punto sin cortarlos.
El radio de la circunferencia inscrita se denomina también inradio.
Cómo determinar el incentro
Para localizar el incentro, se deben trazar las bisectrices de cada ángulo interior del triángulo.
La bisectriz de un ángulo es la recta que divide un ángulo en dos partes exactamente iguales.
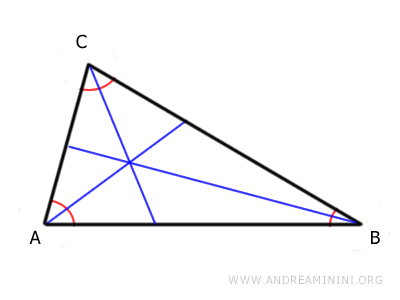
El punto en el que se cruzan las bisectrices (I) recibe el nombre de incentro y siempre se halla en el interior del triángulo.
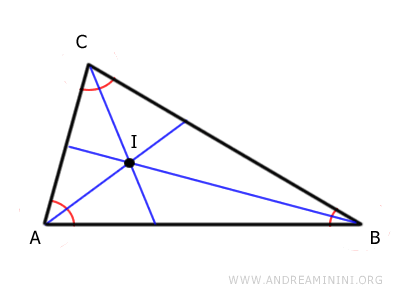
Finalmente, se traza un segmento perpendicular (ID) desde el incentro (I) hasta uno de los lados del triángulo. En este ejemplo, se ha elegido el lado AB.
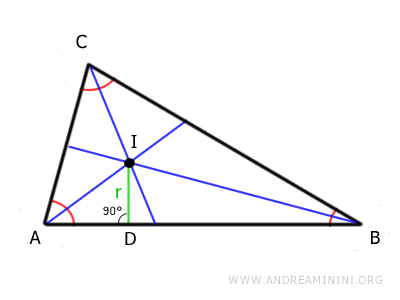
Este segmento se conoce como inradio y constituye el radio de la circunferencia inscrita en el triángulo (la circunferencia inscrita).
El centro de esta circunferencia es precisamente el incentro.
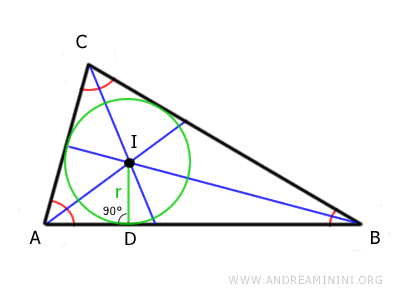
Una característica esencial de la circunferencia inscrita es que es tangente a los tres lados del triángulo.
La demostración
Consideremos el triángulo ABC.
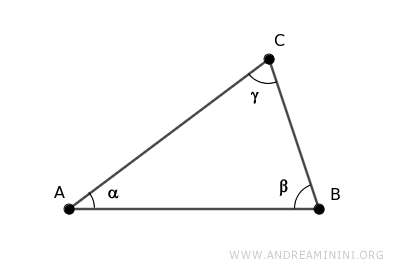
Se trazan las bisectrices de los ángulos α y β.
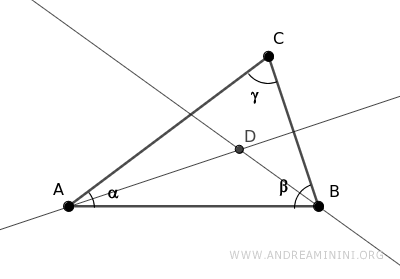
Sabemos que la suma de los ángulos de cualquier triángulo es siempre 180° (un ángulo llano),
$$ \alpha + \beta + \gamma = 180° $$
por lo que podemos concluir que la suma de los ángulos α y β es necesariamente menor que 180°.
$$ \alpha + \beta < 180° $$
En consecuencia, la suma de la mitad de los ángulos α y β también es menor que 180°, lo cual garantiza que las bisectrices de estos dos ángulos se crucen en un punto D.
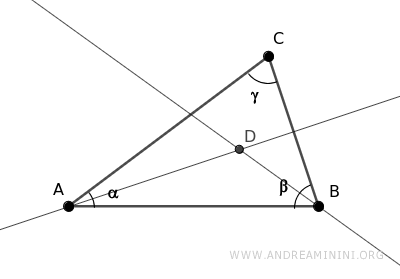
Desde el punto D se trazan segmentos perpendiculares hacia los lados del triángulo.
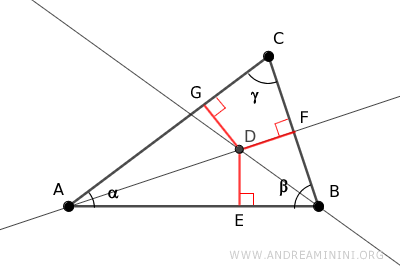
Los segmentos DE y DF son congruentes porque el punto D está situado sobre la bisectriz del ángulo β, lo cual implica que se encuentra a la misma distancia de los lados que forman dicho ángulo.
$$ \overline{DE} \cong \overline{DF} $$
De modo análogo, los segmentos DE y DG también son congruentes, ya que el punto D está sobre la bisectriz del ángulo α, por lo que se halla equidistante de sus lados.
$$ \overline{DE} \cong \overline{DG} $$
Por la propiedad transitiva, si DE ≅ DF y DE ≅ DG, entonces los segmentos DF ≅ DG también son congruentes.
$$ \overline{DF} \cong \overline{DG} $$
Esto significa que el punto D se encuentra a igual distancia de los lados que forman el ángulo γ, por lo cual pertenece a la bisectriz de dicho ángulo.
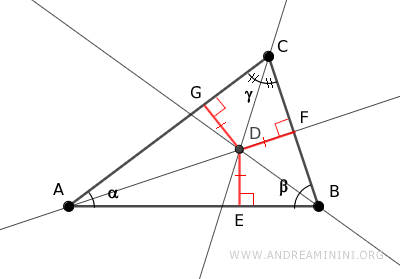
Esto demuestra que el punto D está situado sobre las tres bisectrices de los ángulos del triángulo.
Observaciones
A continuación, se presentan algunas observaciones y propiedades sobre el incentro:
- En todo triángulo es posible inscribir una circunferencia cuyo centro es el incentro.
- El incentro está a la misma distancia de los tres lados del triángulo. Esta distancia corresponde al radio de la circunferencia inscrita.
- La posición del incentro varía en función de la forma del triángulo. Por ejemplo, en un triángulo equilátero, el incentro coincide con el baricentro, el circuncentro y el ortocentro.
- El incentro divide cada bisectriz en dos segmentos cuya longitud es proporcional a los lados adyacentes al vértice correspondiente.
- La circunferencia inscrita (incircle), cuyo centro es el incentro, es tangente a los tres lados del triángulo.
Y así sucesivamente.