Triángulo

Un triángulo es un polígono de tres lados, definido por sus tres ángulos.

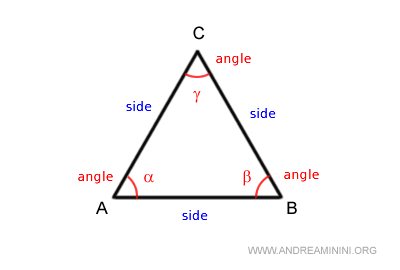
Descripción general

El triángulo, una de las figuras fundamentales de la geometría euclidiana, está delimitado por una línea poligonal cerrada que une tres puntos no colineales.

Sus vértices, denominados vértices, están representados por tres puntos distintos (A, B, C) que no se encuentran alineados.

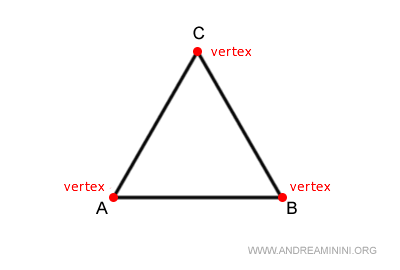
Un vértice se denomina vértice opuesto a un lado cuando no pertenece a dicho lado.

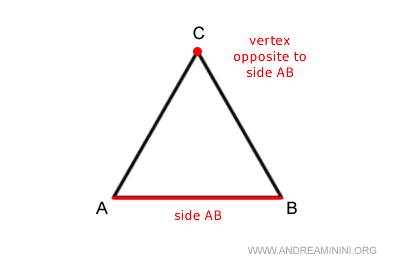
Cada par de lados de un triángulo forma un ángulo interior, cuyo vértice es común a ambos lados.

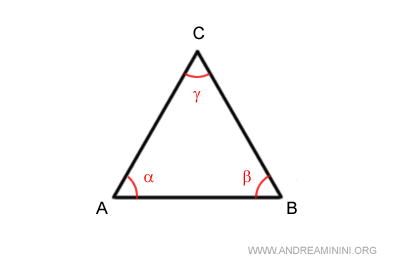
Un ángulo se considera adyacente a un lado si su vértice coincide con uno de los extremos del lado y uno de sus lados (o brazos) se extiende a lo largo de él.

Por ejemplo, el ángulo β es adyacente tanto al lado AB como al lado BC.

 

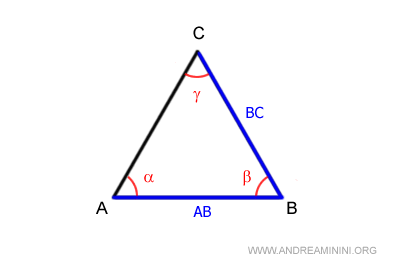
Por lo tanto, cada lado del triángulo está flanqueado por dos ángulos adyacentes.

Así, los ángulos α y β son adyacentes al lado AB.

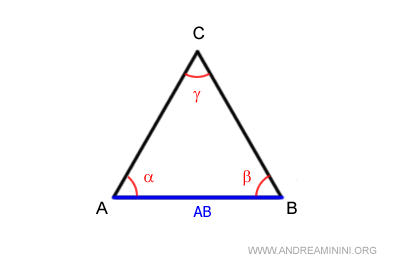
Un ángulo se denomina ángulo opuesto a un lado cuando no es adyacente a él.

Por ejemplo, el ángulo γ es opuesto al lado AB.

 

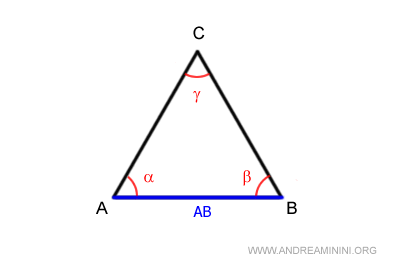
Independientemente de la forma del triángulo, la suma de sus ángulos interiores siempre es igual a 180°.

$$ \alpha + \beta + \gamma = 180° $$

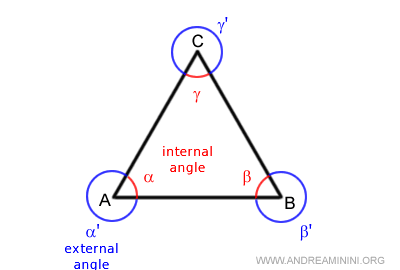
A cada ángulo interior le corresponde un ángulo exterior complementario.

El término “triángulo” proviene de los vocablos griegos que significan “tres” y “ángulo”. Se trata de una figura geométrica de gran versatilidad, presente en numerosos campos como la física y las matemáticas. Desempeña un papel esencial en la trigonometría, que estudia las relaciones entre los lados y los ángulos del triángulo.

Tipos de triángulo

Los triángulos pueden clasificarse de diversas maneras, cada una destacando propiedades y características particulares de la figura.

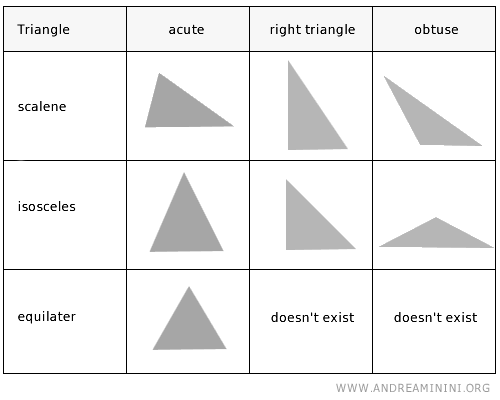
Según sus lados:

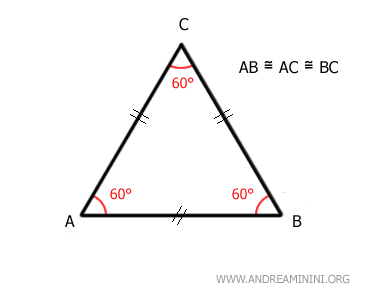
• Triángulo equilátero
  Es un triángulo cuyos tres lados son de igual longitud, lo que implica que sus tres ángulos interiores miden 60 grados.
  
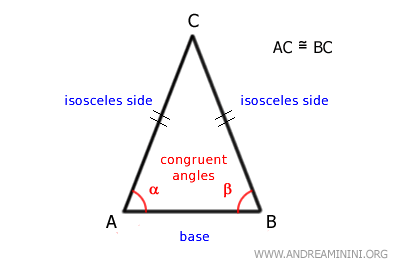
• Triángulo isósceles
  Se caracteriza por tener dos lados de igual longitud, y por lo tanto, dos ángulos adyacentes a la base también iguales.
  

  

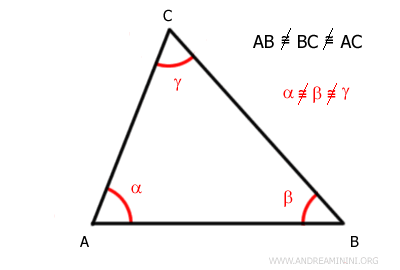
• Triángulo escaleno
  Es un triángulo cuyos tres lados son desiguales; en consecuencia, sus tres ángulos también son diferentes, lo que le confiere una forma asimétrica.
  

Según sus ángulos:

• Triángulo acutángulo
  Es aquel cuyos tres ángulos interiores son menores de 90 grados, lo que le confiere un aspecto esbelto y agudo.
  
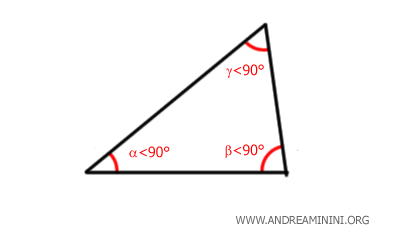
• Triángulo obtusángulo
  Se caracteriza por tener un único ángulo mayor de 90 grados, que le otorga una apariencia amplia y abierta.
  
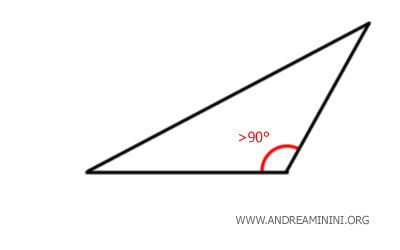
• Triángulo rectángulo
  El clásico triángulo rectángulo se reconoce por su ángulo recto (de 90 grados), y constituye la base de la trigonometría.
  

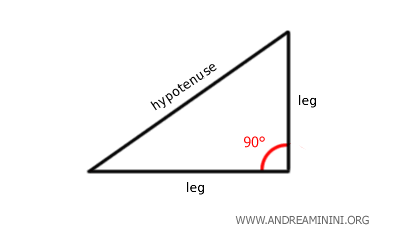
  En el triángulo rectángulo, los lados que forman el ángulo recto se denominan catetos, mientras que el lado opuesto al ángulo recto se conoce como hipotenusa.

Fórmulas del triángulo

Entre las principales fórmulas para calcular distintas propiedades de un triángulo destacan:

• Área
  El área (A) de un triángulo se obtiene multiplicando la base (b) por la altura (h) y dividiendo entre dos: $$ A = \frac{\text{b} \cdot \text{h}}{2} $$.

  Si únicamente se conocen las longitudes de los lados, se puede utilizar la fórmula de Herón: $$ A = \sqrt{p(p-l_1)(p-l_2)(p-l_3)} $$ donde \( l_1 \), \( l_2 \) y \( l_3 \) son los lados, y \( p = \frac{l_1+l_2+l_3}{2} \) es el semiperímetro del triángulo.

• Perímetro
  El perímetro (P) es la suma de las longitudes de los tres lados: $$ P = a + b + c $$, siendo a, b y c las longitudes de los lados.

Los triángulos isósceles y equiláteros disponen de fórmulas específicas para calcular su área y perímetro.

Centros del triángulo

Los triángulos poseen varios centros notables: baricentro, ortocentro, incentro y circuncentro, entre otros.

• Ortócentro
  Es el punto donde se cortan las tres alturas del triángulo.
  

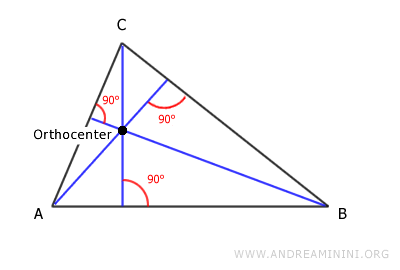
  Nota: Todo triángulo tiene tres alturas. Según el tipo de triángulo, el ortocentro puede situarse en el interior, en el exterior o en un vértice: queda en el exterior en un triángulo escaleno obtusángulo, en el interior en un escaleno acutángulo, y en el vértice del ángulo recto en un triángulo rectángulo.

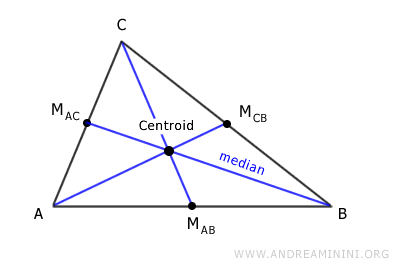
• Baricentro
  Es el punto de intersección de las tres medianas del triángulo; siempre se halla en su interior.
  
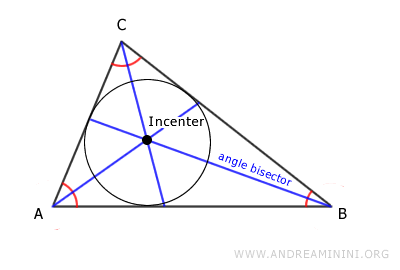
• Incentro
  Punto de intersección de las tres bisectrices de los ángulos interiores; constituye el centro de la circunferencia inscrita.
  
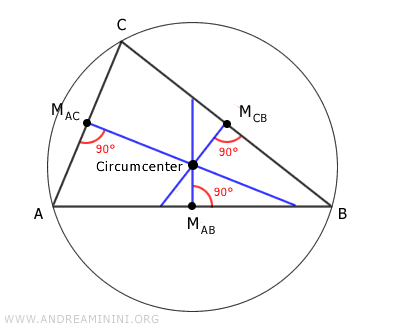
• Circuncentro
  Punto donde se cortan las tres mediatrices de los lados, que actúa como centro de la circunferencia circunscrita.
  

 

El ortocentro, el baricentro, el incentro y el circuncentro de un triángulo son puntos concíclicos que pertenecen al círculo de Euler.

Propiedades del triángulo

Veamos algunas de las principales propiedades geométricas de los triángulos:

• La suma de los ángulos interiores de cualquier triángulo es 180°
  Es decir, los tres ángulos interiores siempre suman un ángulo llano: $$ \alpha + \beta + \gamma = 180° $$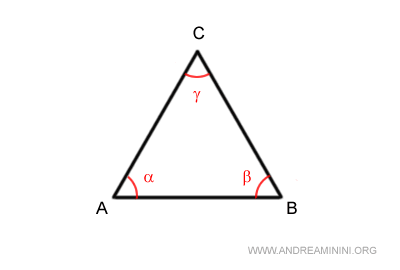

  

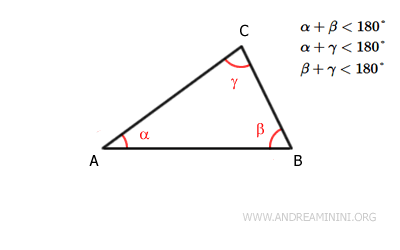
• La suma de dos ángulos interiores siempre es menor que 180°
  Cualquier par de ángulos interiores de un triángulo siempre suma menos de 180°.
  
• Todo triángulo tiene al menos dos ángulos agudos
  En cualquier triángulo, siempre hay al menos dos ángulos agudos, pues no puede haber más de un ángulo obtuso o recto. Si los hubiera, su suma excedería los 180°, contradiciendo la propiedad fundamental.

  Demostración. Si un triángulo contiene un ángulo recto (90°), los otros dos deben sumar 90°, y por tanto serán agudos. Si el triángulo tiene un ángulo obtuso, los dos restantes sumarán menos de 90°, siendo ambos agudos. Así, en cualquier triángulo al menos dos de sus ángulos deben ser agudos.

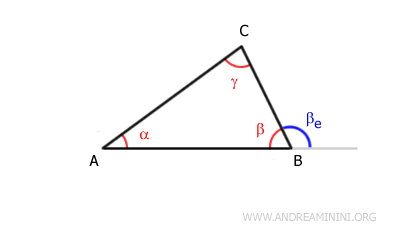
• Teorema del ángulo exterior
  Cualquier ángulo exterior (β_e) de un triángulo es mayor que cada uno de los ángulos interiores no adyacentes (α y γ).
  
• Teorema de Pitágoras
  En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
• Todo triángulo admite una circunferencia inscrita
  Las bisectrices de los ángulos interiores siempre se cortan en un punto (incentro), equidistante de los lados, centro de la circunferencia inscrita.
  
• Todo triángulo puede ser circunscrito por una circunferencia
  Las mediatrices de los lados se cortan en el circuncentro, equidistante de los vértices y centro de la circunferencia circunscrita.
  

  Nota: En un triángulo equilátero, existe una relación constante entre el radio de la inscrita (r) y el de la circunscrita (R): $$ r = \frac{1}{3} \cdot R $$ ya que en este caso baricentro, ortocentro, circuncentro e incentro coinciden en un mismo punto.
  
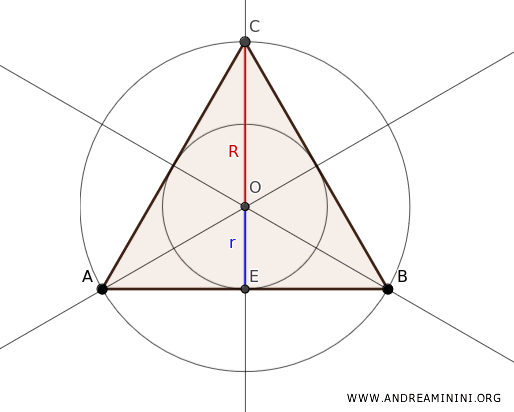
  Como el baricentro divide cada mediana en segmentos en razón 2:1, se tiene que $ R = 2r $, de modo que $ h = r + R $, y por tanto $ r = \frac{1}{3} R $.

• Todo triángulo posee un único baricentro, punto de equilibrio donde confluyen sus medianas (segmentos que unen cada vértice con el punto medio del lado opuesto).
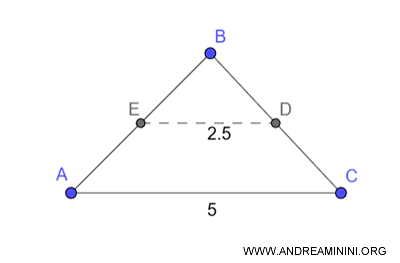
• El segmento que une los puntos medios de dos lados de un triángulo es paralelo al tercer lado y mide la mitad de su longitud
  El segmento $ED$, que conecta los puntos medios de los lados $AB$ y $BC$ de un triángulo, es paralelo al tercer lado $AC$ y tiene exactamente la mitad de su medida.
  
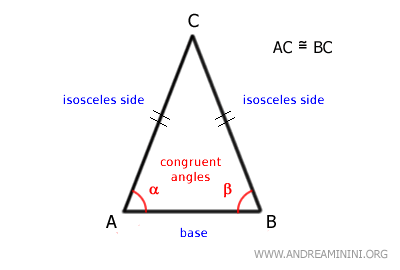
• Teorema del triángulo isósceles
  En un triángulo con dos lados congruentes, los ángulos opuestos a dichos lados también son congruentes. 

  Ejemplo. En un triángulo isósceles, la igualdad de dos lados implica la igualdad de los ángulos de la base. La altura desde el vértice opuesto a la base actúa como eje de simetría, dividiendo el triángulo en dos triángulos rectángulos congruentes.
  

Y estas son solo algunas de las muchas propiedades que caracterizan a los triángulos.