Teorema del triángulo isósceles
Un triángulo es isósceles si y solo si tiene dos ángulos de base congruentes.
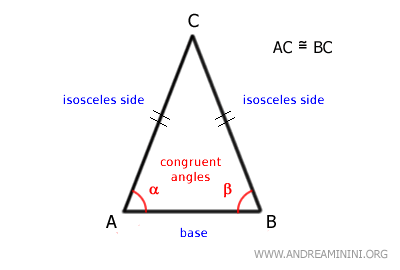
Esto se debe a que, en todo triángulo, los lados opuestos a ángulos iguales también son iguales.
Por tanto, si un triángulo es isósceles, necesariamente tiene dos ángulos congruentes.
Y viceversa: si un triángulo tiene dos ángulos iguales, entonces debe ser isósceles.
En resumen: tener dos ángulos iguales en la base constituye una condición necesaria y suficiente para que un triángulo sea isósceles.
Demostración directa
Consideremos un triángulo isósceles.
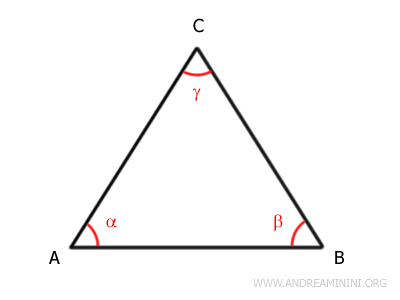
Por definición, posee dos lados de igual longitud:
$$ \overline{AC} \cong \overline{BC} $$
En este caso, AC y BC son los lados congruentes, mientras que AB es la base.
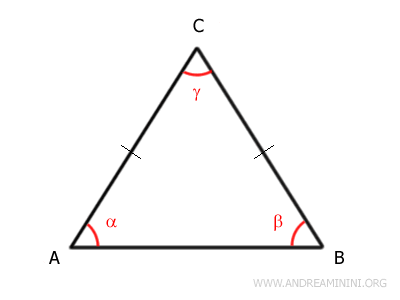
Queremos probar que los ángulos de la base también son congruentes.
Para ello, trazamos la bisectriz del ángulo del vértice, CD, dividiéndolo en dos ángulos iguales: γ1 y γ2.
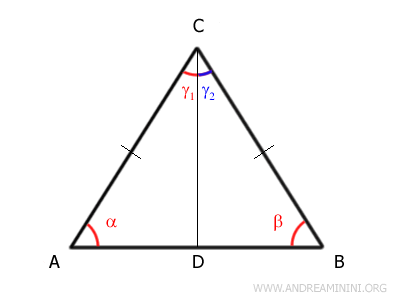
Esto genera dos triángulos rectángulos: ACD y BCD.
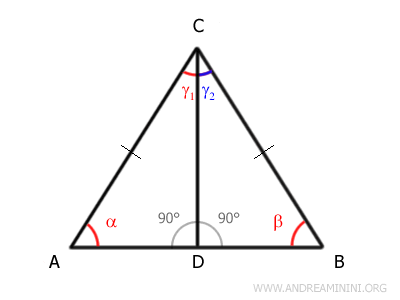
Según el primer criterio de congruencia (lado-ángulo-lado), estos triángulos son congruentes porque:
- Comparten el lado CD: $$ \overline{CD} \cong \overline{CD} $$
- Los lados AC y BC son congruentes por hipótesis: $$ \overline{AC} \cong \overline{BC} $$
- Los ángulos γ1 y γ2 son iguales por construcción: $$ \gamma_1 \cong \gamma_2 $$
De la congruencia de ACD y BCD se deduce que todos los elementos correspondientes son congruentes, incluidos los ángulos de la base:
$$ \alpha \cong \beta $$
Hemos demostrado así que todo triángulo isósceles tiene dos ángulos iguales en la base.
Demostración de la recíproca
Veamos ahora que si un triángulo tiene dos ángulos congruentes, entonces necesariamente es isósceles.
Consideramos un triángulo en el que α y β son congruentes:
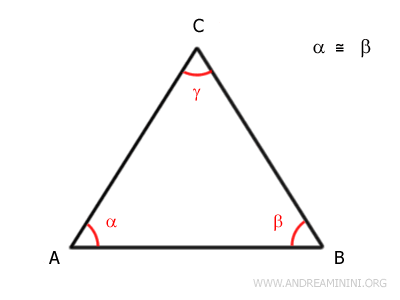
Queremos demostrar que esto implica que los lados opuestos a dichos ángulos también son iguales.
Prolongamos los lados AC y BC añadiendo segmentos congruentes: AD ≅ BE.
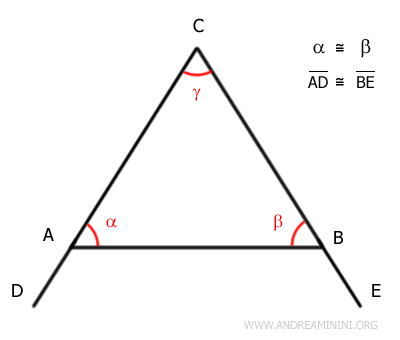
Definimos dos nuevos ángulos, α' y β', suplementarios a α y β respectivamente.
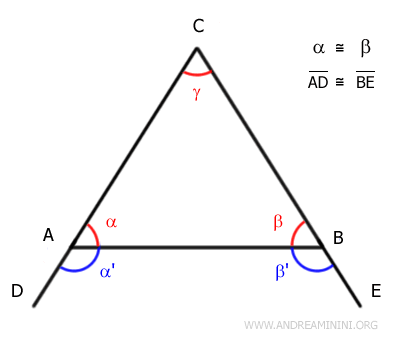
Dado que α = β, también se cumple que α' = β'.
Unimos A con E y B con D para formar los triángulos ABE y ABD.
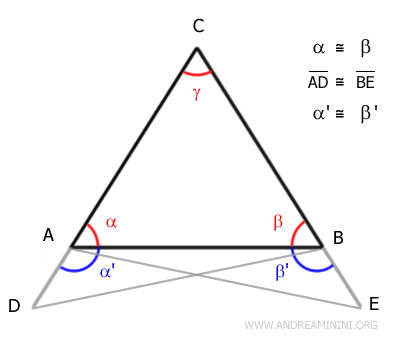
Aplicando el primer criterio de congruencia (lado-ángulo-lado), se concluye que:
$$ ABD \cong ABE $$
Por tanto, los lados BD y AE son iguales:
$$ \overline{BD} = \overline{AE} $$
También los ángulos δ y ε son congruentes:
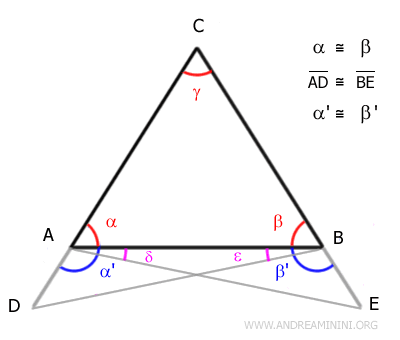
Y lo mismo ocurre con θ y σ:
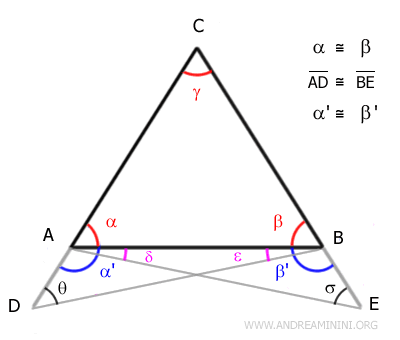
Sumando ángulos congruentes obtenemos:
$$ \alpha + \delta \cong \beta + \epsilon $$
Esto implica la congruencia de los triángulos ACE y BCD:
$$ ACE \cong BCD $$
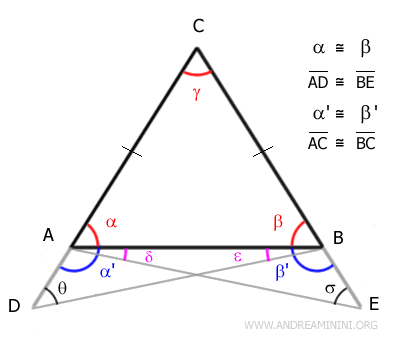
Por lo tanto, los lados AC y BC deben ser congruentes:
$$ \overline{AC} \cong \overline{BC} $$
Así queda demostrado que el triángulo ABC es isósceles.
Demostración alternativa
Tomemos un triángulo con dos ángulos iguales, \( \alpha \cong \beta \).

Se trazan las bisectrices de \( \alpha \) y \( \beta \).
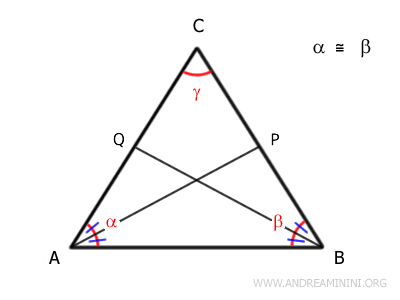
Como los ángulos son iguales, también lo son sus mitades:
\[ A\widehat{B}Q \cong C\widehat{B}Q \cong B\widehat{A}P \cong C\widehat{A}P \]
Los triángulos \( ABQ \) y \( ABP \) son congruentes por el criterio ángulo-lado-ángulo (ALA).
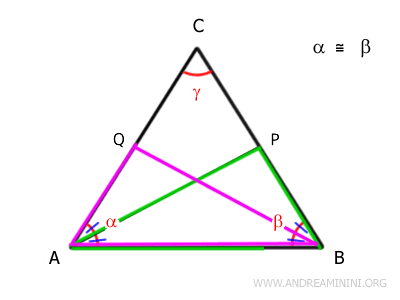
Entonces, \( AP = BQ \) y \( A\widehat{Q}B = B\widehat{P}A \).
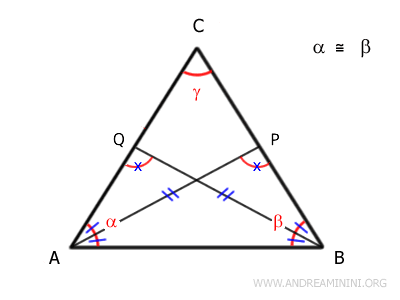
Sus ángulos suplementarios también son congruentes:
\[ C\widehat{P}A = C\widehat{Q}B \]
Examinamos ahora los triángulos \( APC \) y \( BQC \):
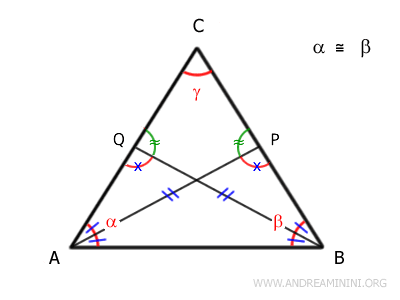
Estos son congruentes por el criterio ALA, y se deduce que:
\[ AC = BC \]
Con lo cual confirmamos nuevamente que el triángulo \( ABC \) es isósceles.

Demostración completada.