Excentro de un triángulo
El excentro es el punto en el que la bisectriz interna de un ángulo se cruza con las bisectrices externas de los otros dos ángulos no adyacentes del triángulo.
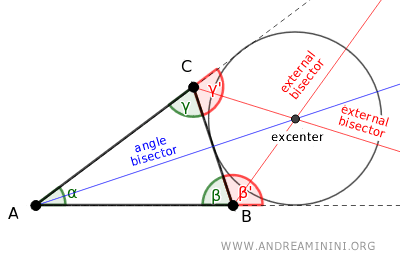
El excentro es el centro de una circunferencia que resulta tangente exteriormente a uno de los lados del triángulo y a las prolongaciones de los otros dos lados.
Todo triángulo posee tres excentros, uno asociado a cada lado.
Por lo tanto, cualquier triángulo tiene tres excircunferencias, cada una tangente exteriormente a un lado y a las prolongaciones de los otros dos.
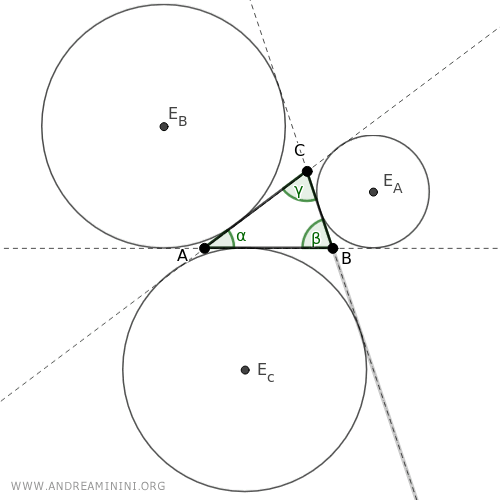
El radio de cada excircunferencia se denomina exradio.
Nota: En el caso de los triángulos equiláteros, todas las excircunferencias tienen el mismo radio.
Cómo localizar el excentro
Se puede determinar el excentro de un triángulo utilizando las bisectrices de sus ángulos.
Consideremos un triángulo ABC.
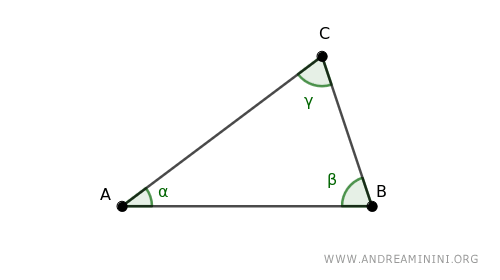
Se traza la bisectriz interna del ángulo γ.
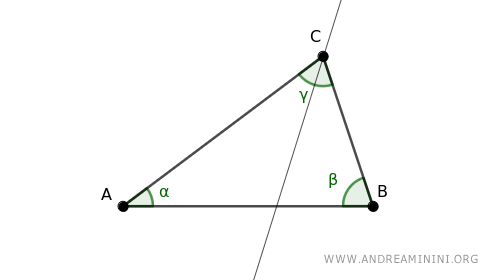
A continuación, se dibujan las bisectrices externas de los ángulos no adyacentes α' y β'.
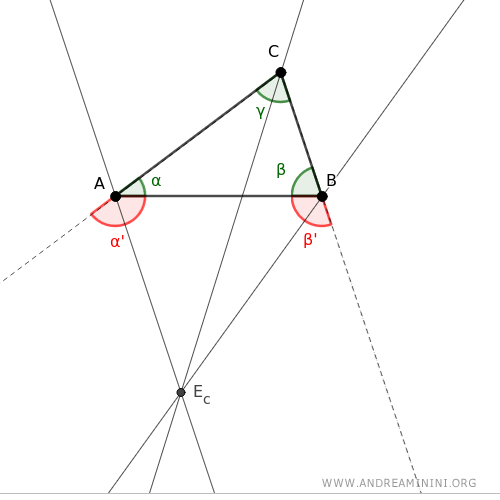
Nota: La bisectriz de un ángulo externo también se denomina bisectriz externa. En ambos casos, es el segmento que divide el ángulo suplementario (180° - α o 180° - β) en dos partes iguales. Por lo tanto, puede hablarse indistintamente de la bisectriz externa del ángulo α' = 180° - α o de la bisectriz externa del ángulo α. El significado es el mismo.
La intersección de la bisectriz interna del ángulo γ con una de las bisectrices externas de los ángulos α o β determina el excentro Ec correspondiente al ángulo γ.
Una vez hallado el excentro, se puede trazar una circunferencia con centro en Ec, tangente exteriormente al lado opuesto AB y a las prolongaciones de los lados AC y BC.
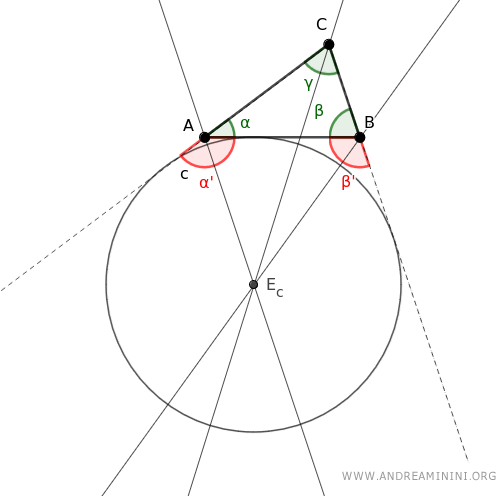
El radio de esta circunferencia se llama exradio correspondiente al ángulo γ.
Nota: En resumen, el excentro de un triángulo respecto a un ángulo concreto se localiza en el punto de intersección entre la bisectriz interna de ese ángulo y las bisectrices externas de los otros dos ángulos.
De forma análoga, los excentros correspondientes a los ángulos α y B se obtienen en los puntos de intersección entre sus respectivas bisectrices internas y las bisectrices externas de los otros dos ángulos.
Por ejemplo, aquí se muestra el excentro correspondiente al ángulo α.
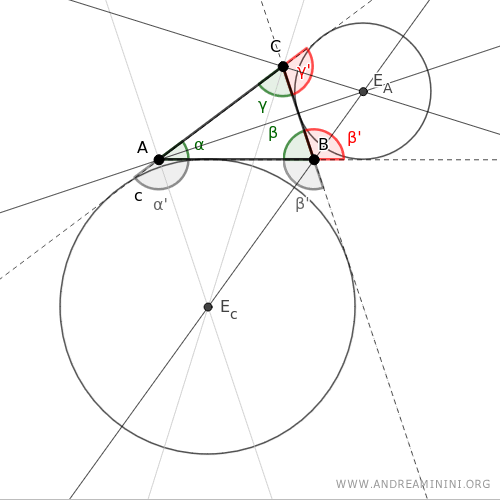
Por último, aquí se muestra el excentro correspondiente al ángulo β.
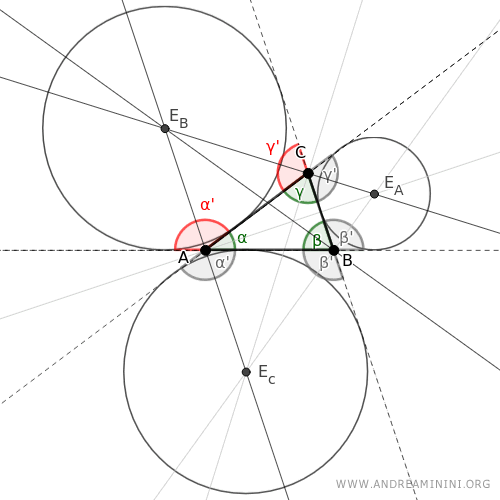
Y así sucesivamente.