Baricentro de un Triángulo

El baricentro de un triángulo es el punto interior donde se intersectan sus medianas.

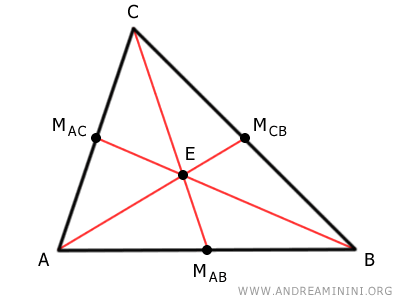
Una mediana de un triángulo es un segmento que conecta un vértice con el punto medio del lado opuesto.

Todo triángulo cuenta con tres vértices (A, B, C) y tres lados (AB, CB, AC), por lo que posee también tres medianas.

Las tres medianas AM_CB, BM_AC y CM_AB se intersectan en un punto interior (E) del triángulo, llamado baricentro.

¿Para qué sirve? El baricentro es, además, el centro de gravedad o de equilibrio del triángulo. El término “baricentro” procede del griego “barys”, que significa “pesado”, y “centro”. Por ejemplo, si se apoyara el triángulo sobre un pequeño soporte colocado exactamente en su baricentro, este permanecería perfectamente equilibrado. En general, el baricentro es de gran utilidad en el estudio del equilibrio de fuerzas sobre una figura o un objeto.

Cómo hallar el baricentro

Consideremos un triángulo cualquiera ABC.

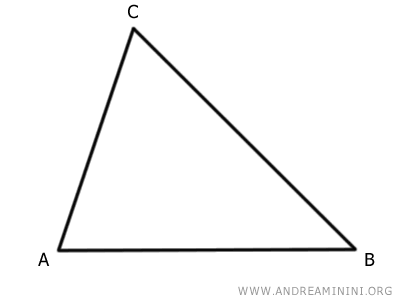
Primero, se determinan los puntos medios de cada uno de los lados del triángulo.

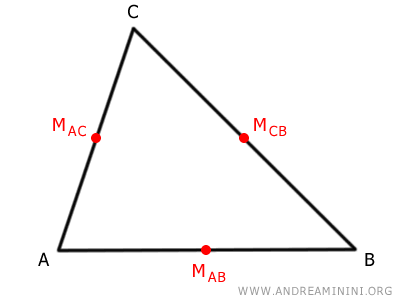
¿Qué es un punto medio? El punto medio de un segmento es el que lo divide en dos partes iguales, es decir, se encuentra a la misma distancia de sus extremos.

Luego, se trazan las tres medianas del triángulo, uniendo cada vértice con el punto medio del lado opuesto.

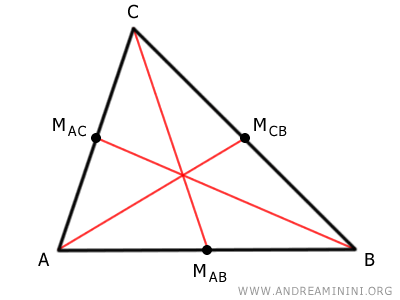
El punto donde se cruzan las medianas (E) se llama baricentro del triángulo.

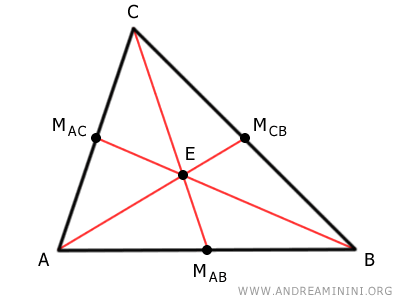
El baricentro divide la mediana en razón 2:1

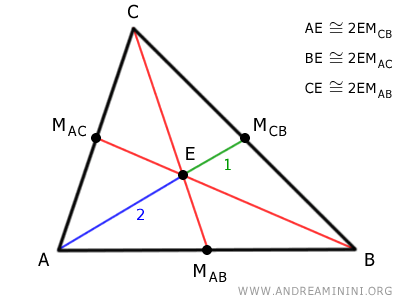
El segmento que va desde el vértice hasta el baricentro mide el doble que el segmento comprendido entre el baricentro y el punto medio del lado opuesto.

Por tanto, el baricentro se ubica a 2/3 de la longitud de la mediana, contados desde el vértice.

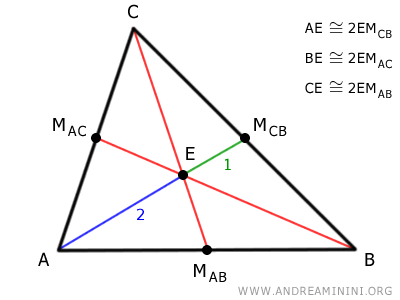
Demostración

Consideremos el triángulo ABC.

Identificamos los puntos medios M y N de dos lados del triángulo y trazamos las medianas correspondientes.

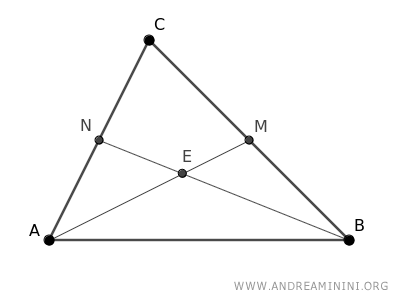
Las dos medianas se cortan en el punto E.

Se determinan los puntos medios de los segmentos AE y BE.

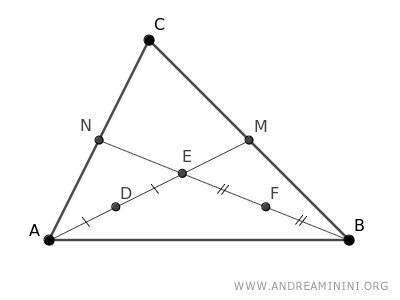
Como son puntos medios, los segmentos AD ≅ ED y BF ≅ EF son congruentes.

$$ \overline{AD} \cong \overline{ED} $$

$$ \overline{BF} \cong \overline{EF} $$

Se traza el segmento que une los puntos medios M y N.

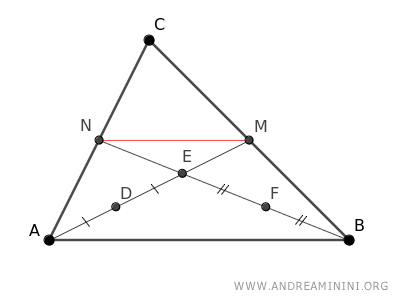
Según el teorema del punto medio, el segmento MN, que conecta dos puntos medios de los lados del triángulo ABC, es paralelo al tercer lado AB y mide la mitad de su longitud.

$$ \overline{MN} \parallel \overline{AB} $$

$$ \overline{MN} \cong \frac{1}{2} \cdot \overline{AB} $$

Se dibuja el segmento DF, que une los puntos medios de los lados del triángulo ABE.

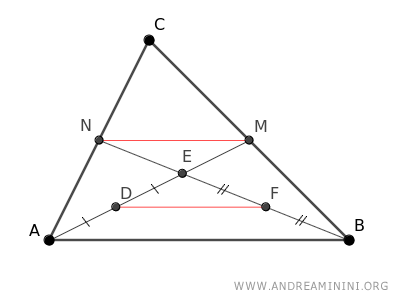
Nuevamente, por el teorema del punto medio, el segmento DF, que conecta dos puntos medios de los lados del triángulo ABE, es paralelo a AB y mide la mitad de su longitud.

$$ \overline{DF} \parallel \overline{AB} $$

$$ \overline{DF} \cong \frac{1}{2} \cdot \overline{AB} $$

Por tanto, los segmentos DF y MN son congruentes y paralelos a AB.

$$ \overline{DF} \cong \overline{MN} \cong \frac{1}{2} \cdot \overline{AB} $$

El cuadrilátero DFMN es un paralelogramo, ya que presenta lados opuestos paralelos (DF || MN) y de la misma longitud (DF ≅ MN).

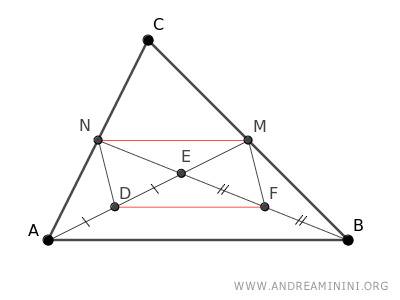
Como las diagonales de un paralelogramo se cortan en sus puntos medios, se deduce que los segmentos EN ≅ EF y ED ≅ EM son congruentes.

$$ \overline{EN} \cong \overline{EF} $$

$$ \overline{ED} \cong \overline{EM} $$

Dado que ED ≅ AD y EF ≅ BF, por la propiedad transitiva se concluye que EN ≅ EF ≅ BF y EM ≅ ED ≅ AD.

De forma gráfica:

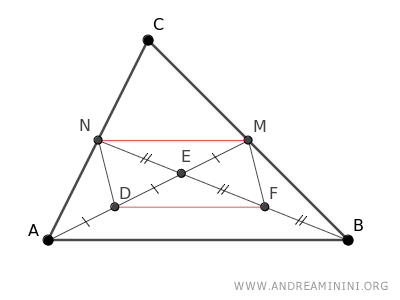
Esto significa que el segmento AE mide el doble que el segmento EM.

$$ \overline{AE} = 2 \overline{EM} $$

De igual modo, el segmento BE es el doble del segmento EN.

$$ \overline{BE} = 2 \overline{EN} $$

Esto demuestra que el baricentro divide cada mediana en dos segmentos en razón 2:1.

Este razonamiento se puede aplicar a cada una de las medianas del triángulo.

El baricentro en geometría analítica

Para encontrar las coordenadas del baricentro \(G(x, y)\) de un triángulo cuyos vértices son \(A(x_1, y_1)\), \(B(x_2, y_2)\) y \(C(x_3, y_3)\) en un sistema de coordenadas cartesianas, se utilizan las siguientes fórmulas: $$ x = \frac{x_1 + x_2 + x_3}{3} $$ $$ y = \frac{y_1 + y_2 + y_3}{3} $$

Estas fórmulas se obtienen calculando el promedio aritmético de las coordenadas \(x\) e \(y\) de los tres vértices del triángulo.

Así, el baricentro se ubica exactamente en el “centro” del triángulo desde el punto de vista de las coordenadas medias de sus vértices.

Ejemplo

Consideremos el siguiente triángulo ABC.

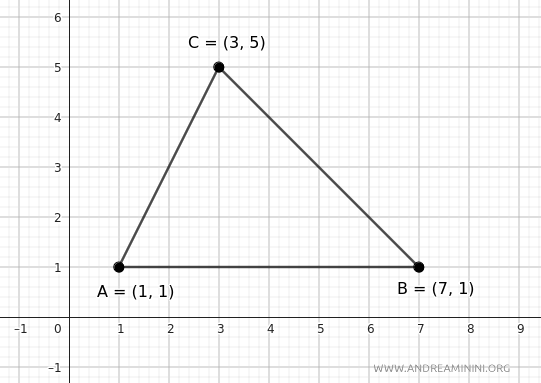
Los vértices del triángulo tienen las siguientes coordenadas cartesianas: A(1,1), B(7,1) y C(3,5).

$$ A(x_1, y_1)= (1,1) $$

$$ B(x_2, y_2)= (7,1) $$

$$ C(x_3, y_3)= (3,5) $$

Para hallar las coordenadas del baricentro G(x,y) del triángulo, se aplican las fórmulas anteriores:

$$ \begin{cases} x = \frac{x_1 + x_2 + x_3}{3} \\ \\ y = \frac{y_1 + y_2 + y_3}{3} \end{cases} $$

Se sustituyen las coordenadas de los vértices A (x₁=1, y₁=1), B (x₂=7, y₂=1) y C (x₃=3, y₃=5).

$$ \begin{cases} x = \frac{1 + 7 + 3}{3} \\ \\ y = \frac{1 + 1 + 5}{3} \end{cases} $$

$$ \begin{cases} x = \frac{11}{3} \\ \\ y = \frac{7}{3} \end{cases} $$

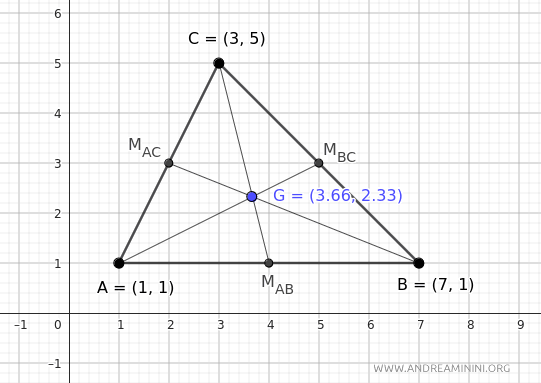
$$ \begin{cases} x = 3.66 \\ \\ y = 2.33 \end{cases} $$

Por tanto, el baricentro G del triángulo se encuentra en las coordenadas (x, y) = (3.66, 2.33).

Demostración

Para demostrar las fórmulas analíticas, consideremos un triángulo ABC.

El baricentro G del triángulo es el punto en el que se intersectan sus medianas.

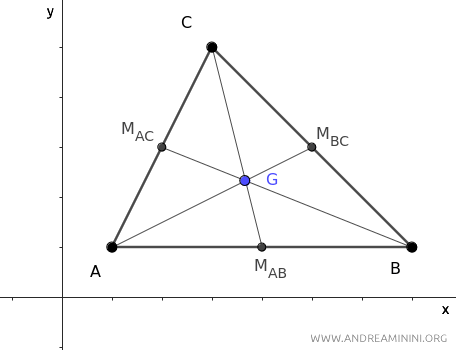
Cada mediana es el segmento que une un vértice del triángulo con el punto medio M del lado opuesto.

El baricentro divide cada mediana en dos partes, de modo que el tramo que va desde el vértice hasta el baricentro mide el doble que el tramo comprendido entre el baricentro y el punto medio del lado opuesto.

Por ejemplo, si consideramos la mediana AM_BC, el segmento AG es el doble del segmento GM_BC.

$$ \overline{AG} = 2 \cdot \overline{GM}_{BC} $$

Ahora proyectamos los puntos A, G y M_BC de la mediana AM_BC sobre el eje x.

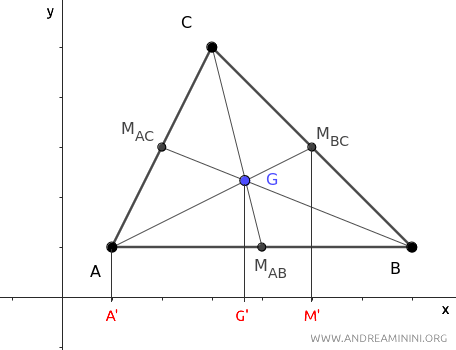
La recta A'M' es la proyección de la mediana AM_BC sobre el eje x del plano cartesiano.

Las proyecciones de estos puntos sobre el eje x determinan un conjunto de rectas paralelas que cortan los dos segmentos transversales AM_BC y A'M'.

De acuerdo con el teorema de Tales, cuando un haz de rectas paralelas corta dos transversales, los segmentos correspondientes en ambas son proporcionales.

Por lo tanto, si el segmento AG es el doble de GM_BC, el segmento proyectado A'G' también será el doble de G'M'.

$$ \overline{A'G'} = 2 \cdot \overline{G'M'} $$

A continuación, expresamos las longitudes de los segmentos proyectados sobre el eje x.

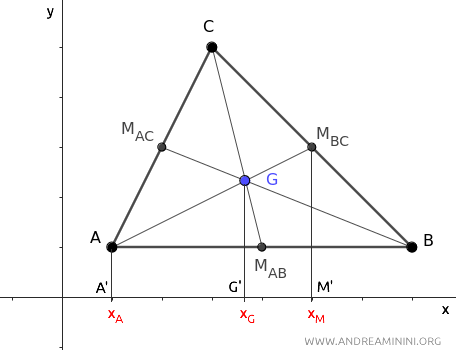
El segmento A'G' mide x_G - x_A, mientras que el segmento G'M' mide x_M - x_G.

Sustituimos estas expresiones en la ecuación anterior:

$$ \overline{A'G'} = 2 \cdot \overline{G'M'} $$

$$ x_G - x_A = 2 \cdot ( x_M - x_G ) $$

$$ x_G - x_A = 2x_M - 2x_G $$

$$ x_G + 2x_G = 2x_M + x_A $$

$$ 3x_G = 2x_M + x_A $$

$$ x_G = \frac{2x_M + x_A}{3} $$

Sabemos que x_M es la proyección sobre el eje x del punto medio M_BC, es decir, $ x_M = \frac{x_B + x_C}{2} $.

$$ x_G = \frac{ 2 \cdot \frac{x_B + x_C}{2} + x_A }{3} $$

$$ x_G = \frac{x_A + x_B + x_C}{3} $$

Esto demuestra la fórmula de la coordenada x del baricentro en el plano cartesiano.

Para demostrar la coordenada y, se sigue un procedimiento análogo.

En este caso, se proyectan los puntos A, G y M_BC de la mediana AM_BC sobre el eje y.

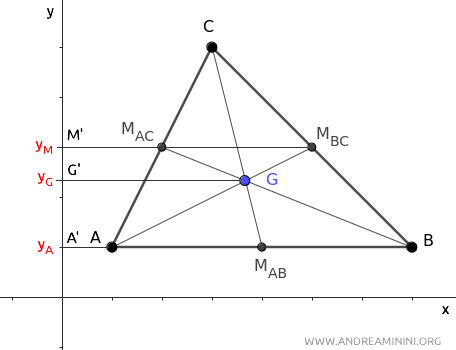
De acuerdo con el teorema de Tales, si el segmento AG mide el doble que GM_BC, entonces el segmento proyectado A'G' sobre el eje y también medirá el doble que G'M'.

$$ \overline{A'G'} = 2 \cdot \overline{G'M'} $$

El segmento A'G' sobre el eje y mide y_G - y_A, mientras que el segmento G'M' mide y_M - y_G.

$$ y_G - y_A = 2 \cdot ( y_M - y_G ) $$

$$ y_G - y_A = 2y_M - 2y_G $$

$$ y_G + 2y_G = y_A + 2y_M $$

$$ 3y_G = y_A + 2y_M $$

$$ y_G = \frac{y_A + 2y_M}{3} $$

Sabemos que y_M es la proyección sobre el eje y del punto medio M_BC, es decir, $ y_M = \frac{y_B + y_C}{2} $.

$$ y_G = \frac{ y_A + 2 \cdot \frac{y_B + y_C}{2} }{3} $$

$$ y_G = \frac{ y_A + y_B + y_C }{3} $$

Esto demuestra la fórmula para la coordenada y del baricentro de un triángulo en el plano cartesiano.

Observaciones

Algunas observaciones y propiedades sobre el baricentro:

• El baricentro es siempre un punto interior al triángulo.
• Existe un único punto de intersección de las medianas de un triángulo
  Por definición, el baricentro es el punto donde se cortan las medianas. Además, se ha demostrado que el baricentro divide cada mediana en una razón 2:1. Dado que en un segmento solo existe un único punto que puede dividirlo en la razón 2:1, una vez establecido que el punto E sobre la mediana AM_CB cumple esa condición, ese mismo punto E debe dividir también las demás medianas en la misma proporción. No puede haber otro punto que cumpla con esta propiedad. En conclusión, existe un único punto en el triángulo que divide todas las medianas en razón 2:1, y es precisamente el punto de intersección de las medianas.
  
• El baricentro es el centro de gravedad del triángulo
  Es decir, es un punto de equilibrio. Por ejemplo, si se coloca el triángulo sobre un clavo situado exactamente en su baricentro, permanecerá en equilibrio.

  Nota. Conocer la posición del baricentro permite determinar el centro de gravedad de una figura y analizar cómo se distribuyen las fuerzas en ella.

• Cualquier movimiento rígido (como una rotación o una traslación) no altera la posición relativa del baricentro en el interior del triángulo. El baricentro se desplaza o gira conjuntamente con la figura.
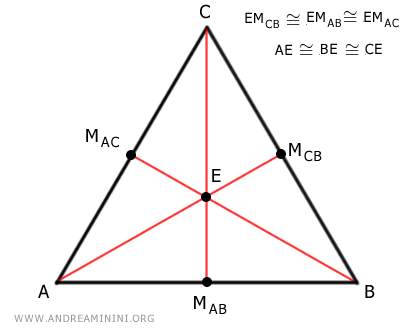
• En el caso particular de un triángulo equilátero, el baricentro coincide con el incentro, el circuncentro y el ortocentro.
  

Y así sucesivamente.