Primer Teorema de los Triángulos Rectángulos
- En un triángulo rectángulo, la longitud de un cateto (b) se determina así:
- multiplicando la hipotenusa (a) por el seno del ángulo (α) opuesto a dicho cateto $$ b = a \cdot \sin \alpha $$
- multiplicando la hipotenusa (a) por el coseno del ángulo agudo (β) adyacente a dicho cateto $$ b = a \cdot \cos \beta $$
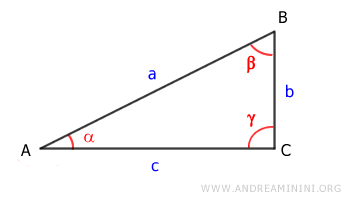
De forma análoga, el otro cateto (c) de un triángulo rectángulo equivale a la hipotenusa (a) multiplicada por el seno del ángulo opuesto (β)
$$ c = a \cdot \sin \beta $$
y también a la hipotenusa (a) multiplicada por el coseno del ángulo adyacente (α)
$$ c = a \cdot \cos \alpha $$
Ejemplo Práctico
Consideremos un triángulo rectángulo.
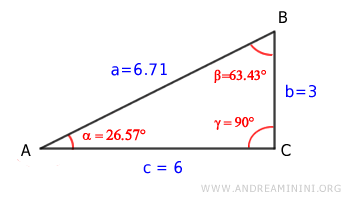
La longitud de la hipotenusa es:
$$ a = \overline{AB} = 6.71 $$
Las longitudes de los catetos son:
$$ b = \overline{BC} = 3 $$
$$ c = \overline{AC} = 6 $$
Los ángulos del triángulo rectángulo son:
$$ \alpha = 26.57° $$
$$ \beta = 63.43° $$
$$ \gamma = 90° $$
Multiplicando la hipotenusa (a) por el seno del ángulo α, obtenemos la longitud del cateto opuesto (b):
$$ 6.71 \cdot \sin (26.57°) = 3 $$
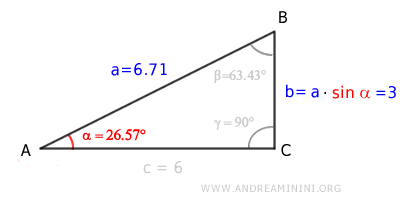
Multiplicando la hipotenusa (a) por el coseno de α, obtenemos la longitud del cateto adyacente (c):
$$ 6.71 \cdot \cos (26.57°) = 6 $$
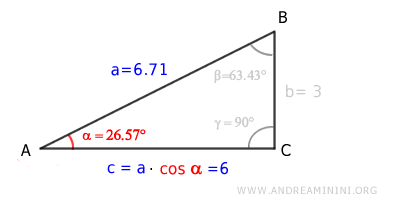
Multiplicando la hipotenusa (a) por el seno del ángulo β, obtenemos la longitud del cateto opuesto (c):
$$ 6.71 \cdot \sin (63.43°) = 6 $$
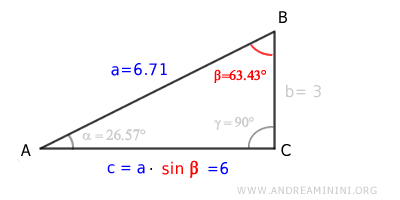
Multiplicando la hipotenusa (a) por el coseno del ángulo β, obtenemos la longitud del cateto adyacente (b):
$$ 6.71 \cdot \cos (63.43°) = 3 $$
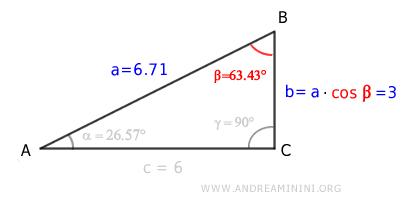
Demostración
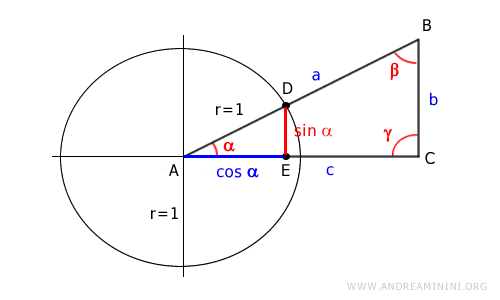
Construyamos un triángulo rectángulo ABC, con el ángulo recto en γ.
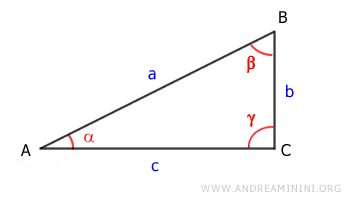
Dibujemos la circunferencia unitaria centrada en el punto A.
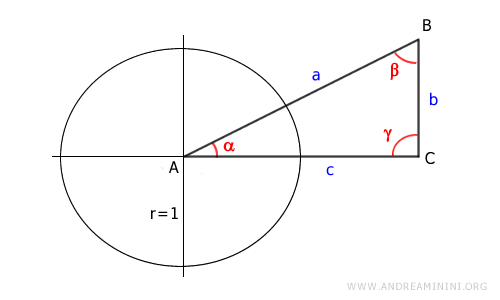
Sea D el punto en el que la hipotenusa del triángulo corta la circunferencia unitaria.
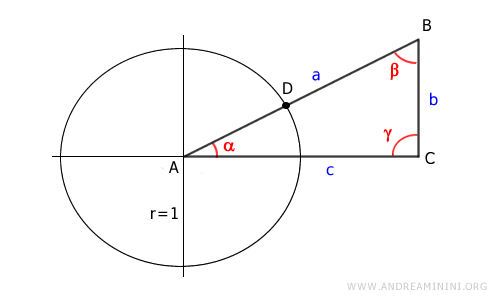
Proyectamos el punto D sobre el eje x (cateto c) y obtenemos el punto E.
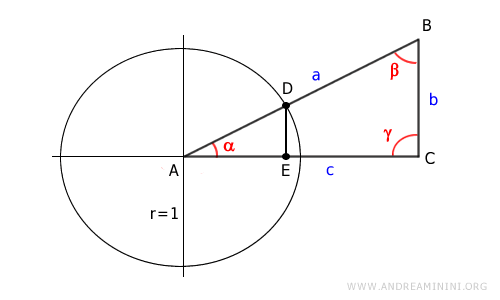
Así se forma otro triángulo rectángulo ADE, inscrito en la circunferencia unitaria.
Los triángulos ABC y ADE son semejantes porque ambos son rectángulos y comparten el ángulo agudo α.
Por ello, podemos establecer las siguientes proporciones:
$$ \overline{BC} : \overline{AB} = \overline{DE} : \overline{AD} $$
$$ \overline{AC} : \overline{AB} = \overline{AE} : \overline{AD} $$
El lado AD corresponde al radio de la circunferencia unitaria, por lo que r = 1.
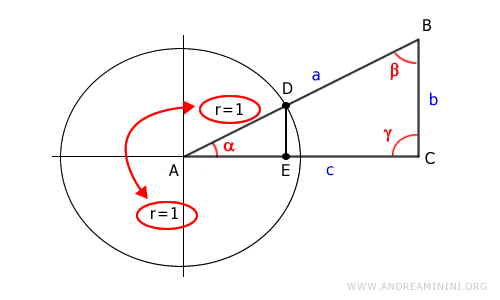
Podemos entonces sustituir AD por 1:
$$ \overline{BC} : \overline{AB} = \overline{DE} : 1 $$
$$ \overline{AC} : \overline{AB} = \overline{AE} : 1 $$
El segmento DE representa el seno del ángulo α.
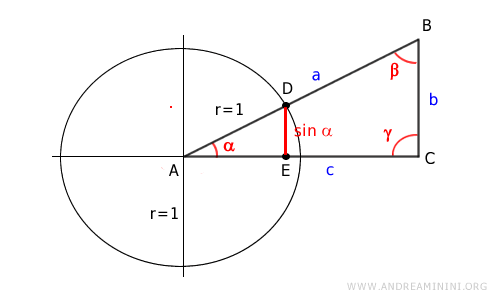
Así, podemos sustituir DE por sen α:
$$ \overline{BC} : \overline{AB} = \sin \alpha : 1 $$
$$ \overline{AC} : \overline{AB} = \overline{AE} : 1 $$
El segmento AE corresponde al coseno del ángulo α.
Por tanto, sustituimos AE por cos α:
$$ \overline{BC} : \overline{AB} = \sin \alpha : 1 $$
$$ \overline{AC} : \overline{AB} = \cos \alpha : 1 $$
Si expresamos estas proporciones en forma de fracción:
$$ \frac{\overline{BC}}{\overline{AB}} = \frac{\sin \alpha}{1} $$
$$ \frac{\overline{AC}}{\overline{AB}} = \frac{\cos \alpha}{1} $$
Despejamos BC y AC:
$$ \overline{BC} = \overline{AB} \cdot \sin \alpha $$
$$ \overline{AC} = \overline{AB} \cdot \cos \alpha $$
Sabiendo que AB = a, BC = b y AC = c, obtenemos:
$$ b = a \cdot \sin \alpha $$
$$ c = a \cdot \cos \alpha $$
En consecuencia, el cateto b equivale a la hipotenusa (a) multiplicada por el seno del ángulo opuesto (α), y el cateto c equivale a la hipotenusa (a) multiplicada por el coseno del ángulo adyacente (α).
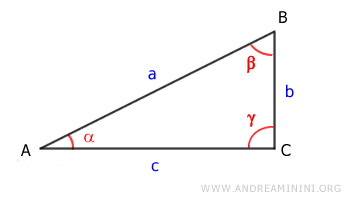
Así queda demostrado el teorema inicial: en un triángulo rectángulo, un cateto es igual al producto de la hipotenusa por el seno del ángulo opuesto, o bien al producto de la hipotenusa por el coseno del ángulo adyacente.
Nota: Como consecuencia directa de este teorema, el lado c también se puede calcular multiplicando la hipotenusa (a) por el seno del ángulo opuesto (β) al cateto $$ c = a \cdot \sin \beta $$ y el lado b se obtiene multiplicando la hipotenusa (a) por el coseno del ángulo adyacente (β) al cateto $$ b = a \cdot \cos \beta $$
Así, todas las fórmulas quedan demostradas.
Y así sucesivamente.