Bisectriz de un Ángulo de un Triángulo
En un triángulo, la bisectriz de un ángulo es el segmento que divide dicho ángulo en dos partes exactamente iguales. Parte del vértice del ángulo y llega hasta un punto situado sobre el lado opuesto.
Todo triángulo posee tres bisectrices de ángulo, una correspondiente a cada vértice.
Por ejemplo, consideremos el triángulo ABC.
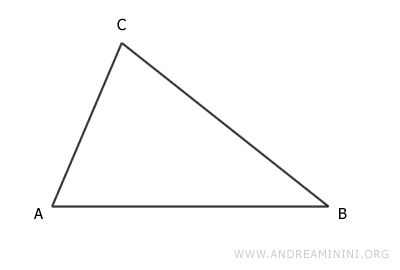
La bisectriz del ángulo en el vértice A es el segmento que divide en dos partes iguales el ángulo formado en A.
Dicho segmento, AM, une el vértice A con un punto M ubicado sobre el lado opuesto, CB.
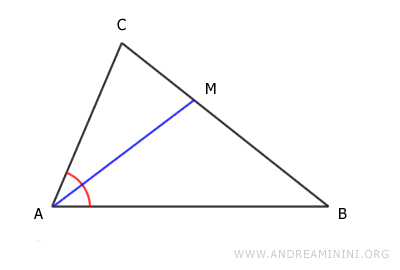
Nota: A diferencia de la bisectriz de un ángulo, que se define como un rayo, la bisectriz de un vértice en un triángulo es un segmento. Consulta la bisectriz de ángulo para comparar.
La bisectriz del ángulo en el vértice B es el segmento BM, que divide el ángulo en B en dos partes iguales y conecta el vértice B con un punto M sobre el lado opuesto, AC.
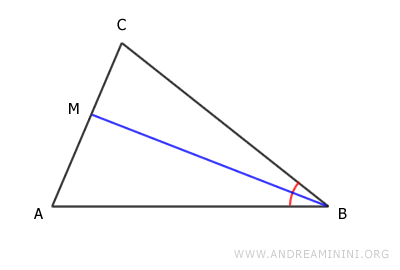
De forma análoga, la bisectriz del ángulo en el vértice C es el segmento CM, que divide el ángulo en C en dos partes idénticas y enlaza el vértice C con un punto M sobre el lado opuesto, AB.
Las tres bisectrices de los ángulos de un triángulo se intersecan en un punto denominado incentro.
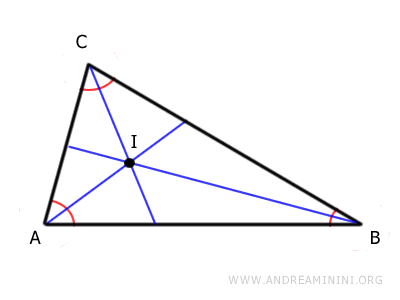
El incentro es el centro de un círculo llamado circunferencia inscrita, que es tangente a los tres lados del triángulo.
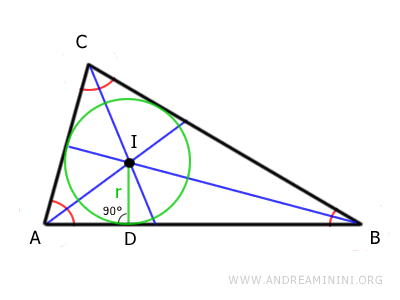
El radio de la circunferencia inscrita se denomina inradio.
Y así sucesivamente.