Triángulo Rectángulo

Un triángulo rectángulo es un triángulo que posee un ángulo recto (90°).

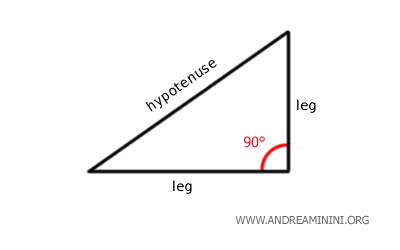
En un triángulo rectángulo, los lados que forman el ángulo recto se denominan catetos.

El lado opuesto al ángulo recto se llama hipotenusa.

El triángulo rectángulo es una de las figuras geométricas más simples, pero constituye el pilar de numerosos teoremas, de la trigonometría y de un sinfín de aplicaciones prácticas.

El interés por el triángulo rectángulo se remonta a las civilizaciones antiguas. Los egipcios lo emplearon en la construcción de las pirámides. Los astrónomos babilonios elaboraban tablas trigonométricas para sus cálculos celestes. Los griegos, como Hiparco, impulsaron aún más el desarrollo de la trigonometría. El célebre matemático griego Pitágoras dio nombre a uno de los teoremas más famosos: el teorema de Pitágoras.

Teorema de Pitágoras

En un triángulo rectángulo, la suma de las áreas de los cuadrados construidos sobre los catetos es igual al área del cuadrado trazado sobre la hipotenusa.

$$ a^2 + b^2 = c^2 $$

Donde "a" y "b" son las longitudes de los catetos, y "c" es la longitud de la hipotenusa.

En otras palabras, el área del cuadrado sobre la hipotenusa equivale a la suma de las áreas de los cuadrados sobre los catetos.

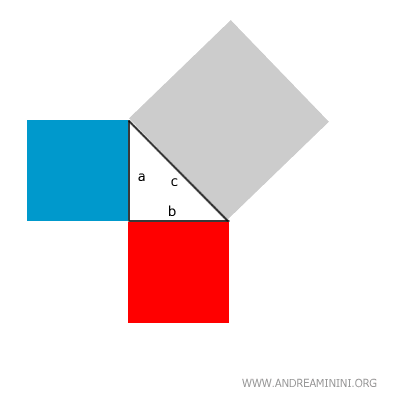
Esto significa que la hipotenusa es siempre el lado más largo de un triángulo rectángulo.

Si extraemos raíz cuadrada en ambos miembros

$$ \sqrt{c^2} = \sqrt{a^2 + b^2} $$

y simplificamos, obtenemos la forma más conocida del teorema:

$$ c = \sqrt{a^2 + b^2} $$

Esta fórmula supuso una auténtica revolución en la geometría y sigue teniendo aplicaciones en múltiples campos hoy en día, desde la física hasta la navegación. Por ejemplo, se utiliza para calcular la distancia entre dos puntos.

Altura de un Triángulo Rectángulo Respecto a la Hipotenusa

La altura de un triángulo rectángulo respecto a la hipotenusa se obtiene multiplicando los catetos (a×b) y dividiendo el resultado entre la hipotenusa (c): $$ h = \frac{a \times b}{c} $$ donde \( a \) y \( b \) representan las longitudes de los catetos, y \( c \) la longitud de la hipotenusa.

Este resultado se deduce del hecho de que el área del triángulo puede expresarse de distintas maneras.

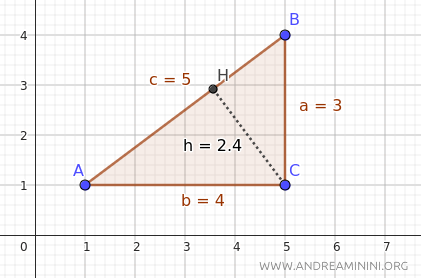
Ejemplo

Veamos como ejemplo este triángulo rectángulo, del cual conocemos las longitudes de todos sus lados.

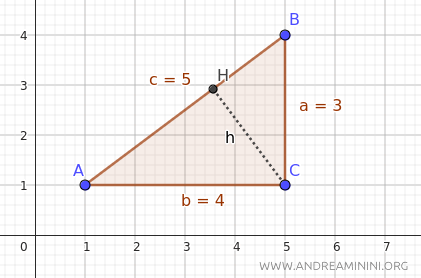
Queremos calcular la altura (h) respecto a la hipotenusa (c).

Para ello, aplicamos la siguiente fórmula:

$$ h = \frac{a \times b}{c} $$

En este caso, los catetos miden a=3, b=4 y la hipotenusa c=5.

$$ h = \frac{3 \times 4}{5} $$

$$ h = \frac{12}{5} $$

$$ h = 2.4 $$

La altura respecto a la hipotenusa es, aproximadamente, h=2.4.

Este resultado ha sido verificado con GeoGebra.

Demostración

Vamos a demostrar la fórmula de la altura respecto a la hipotenusa:

$$ h = \frac{a \times b}{c} $$

En general, la altura (h) de un triángulo (no solo en los rectángulos) respecto a cualquiera de sus lados considerados como base se obtiene mediante la fórmula:

$$ h = \frac{2 \cdot A}{\text{base}} $$

Donde A es el área del triángulo y "base" es la longitud del lado que se toma como referencia.

El área de un triángulo rectángulo equivale a la mitad del producto de la base por la altura.

$$ A = \frac{\text{base} \times \text{altura}}{2} $$

En un triángulo rectángulo, podemos elegir un cateto como "base" y el otro como "altura."

Así, el área del triángulo es: $$ A = \frac{a \cdot b}{2} $$

Sustituyendo el valor de A en la fórmula inicial y simplificando:

$$ h = \frac{2 \cdot A}{\text{base}} $$

$$ h = \frac{2 \cdot ( \frac{a \cdot b}{2} )}{\text{base}} $$

$$ h = \frac{a \cdot b}{\text{base}} $$

Si consideramos la hipotenusa (c) como base:

$$ h = \frac{a \cdot b}{c} $$

Y así obtenemos la fórmula que queríamos demostrar.

La altura (h) de un triángulo rectángulo respecto a la hipotenusa es igual al producto de los catetos dividido entre la hipotenusa.

Este resultado resulta especialmente útil en contextos geométricos más avanzados. Por ejemplo, en geometría analítica, lo he empleado para demostrar la distancia de un punto a una recta en el plano cartesiano.

Demostración Alternativa. Para demostrar que la altura \( h \) de un triángulo rectángulo respecto a la hipotenusa es igual al producto de los catetos dividido entre la hipotenusa, también podemos recurrir a la relación entre el área del triángulo expresada de dos maneras distintas. Consideremos un triángulo rectángulo con catetos de longitudes \( a \) y \( b \), y hipotenusa \( c \). El área \( A \) del triángulo se puede expresar como la mitad del producto de los catetos: $$ A = \frac{1}{2}ab $$ A su vez, el área \( A \) también puede expresarse como la mitad del producto de la hipotenusa \( c \) y la altura \( h \) correspondiente: $$ A = \frac{1}{2}ch $$ Como ambas expresiones representan el área del mismo triángulo, podemos igualarlas: $$ \frac{1}{2}ab = \frac{1}{2}ch $$ Simplificando y eliminando el factor \( \frac{1}{2} \) en ambos lados de la ecuación, y despejando \( h \): $$ ab = ch $$ De donde se obtiene la altura (h): $$ h = \frac{ab}{c} $$ Esto demuestra que la altura \( h \) respecto a la hipotenusa es, efectivamente, el producto de los catetos dividido entre la hipotenusa.

Criterios de Congruencia para Triángulos Rectángulos

Los triángulos rectángulos cumplen con ciertos criterios específicos de congruencia:

• Dos triángulos rectángulos son congruentes si sus catetos son congruentes
  

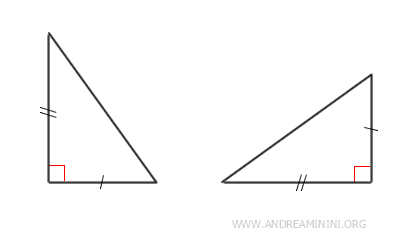
  Demostración: Según el primer criterio de congruencia (LAL), dos triángulos son congruentes si tienen dos lados iguales y el ángulo comprendido entre ellos es congruente. En un triángulo rectángulo, el ángulo formado por los catetos siempre es recto (90°). Por tanto, basta con que los dos catetos sean congruentes para asegurar que los triángulos rectángulos son congruentes.

• Dos triángulos rectángulos son congruentes si tienen un lado congruente y un ángulo agudo congruente

  Demostración: En todo triángulo rectángulo existe un ángulo recto. Si sabemos que un ángulo agudo es congruente, el otro ángulo agudo también lo será, pues la suma de los ángulos interiores siempre es 180°. Conociendo además que uno de los lados es congruente, el segundo criterio generalizado de congruencia (ALA) garantiza que ambos triángulos son congruentes.

• Dos triángulos rectángulos son congruentes si tienen un cateto congruente y la hipotenusa congruente
  

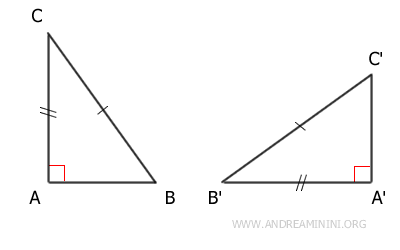
  Demostración: Según la hipótesis inicial, los triángulos ABC y A'B'C' tienen un cateto congruente AB≅A'B' y también hipotenusas congruentes BC≅B'C'. Ahora construyo un triángulo ACD, congruente con A'B'C' y que comparte el cateto AC con el triángulo ABC.
  
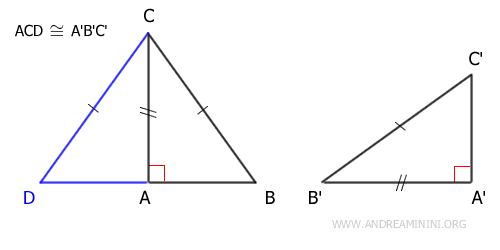
  El triángulo BCD es un triángulo isósceles porque posee dos lados iguales BC≅CD. Por tratarse de un isósceles, tiene también dos ángulos agudos congruentes junto a la base β≅γ.
  
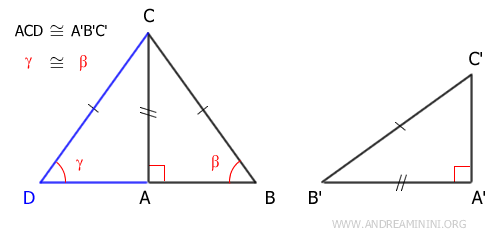
  Así, de acuerdo con el segundo criterio generalizado de congruencia (ALA), los triángulos ACD≅ABC son congruentes, ya que comparten el lado AC, tienen lados iguales BC≅CD y ángulos congruentes β≅γ. Dado que ACD≅A'B'C' por construcción, se deduce por la propiedad transitiva que los triángulos ABC≅A'B'C' son congruentes.
  
  
  Demostración Alternativa
  Consideremos dos triángulos rectángulos, ABC y A'B'C', ambos con ángulos rectos en los vértices B y B'. Supongamos que un cateto es congruente (BC = B'C') y que las hipotenusas también son congruentes (AC = A'C'). Queremos demostrar que los triángulos ABC y A'B'C' son congruentes.
  
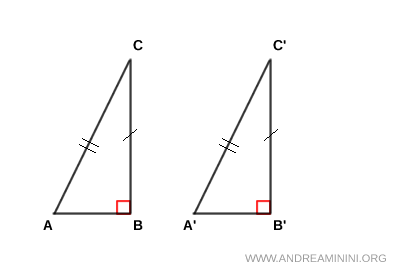
  Prolongamos el segmento A'B' añadiendo un segmento B'D tal que B'D ≅ AB. Luego unimos el punto D con C', formando el triángulo B'C'D. Como el ángulo en B' es suplementario a un ángulo recto, él mismo es recto, de modo que B'C'D es también un triángulo rectángulo.
  
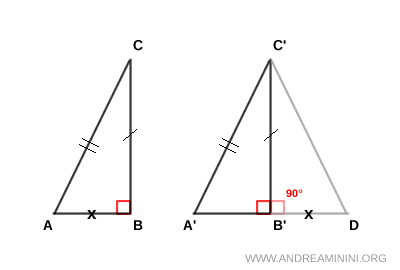
  Por el primer criterio de congruencia (LAL), los triángulos ABC y B'C'D son congruentes, ABC ≅ B'C'D, pues comparten un lado igual (AB ≅ B'D, por construcción), otro lado igual (BC ≅ B'C', por hipótesis) y el ángulo comprendido es recto (90°). Se deduce que AC ≅ C'D.
  
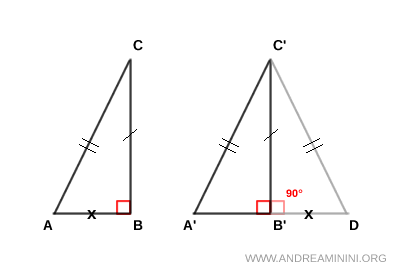
  El triángulo A'C'D es isósceles, ya que tiene dos lados congruentes. En un triángulo isósceles, la altura desde el vértice también coincide con la mediana, por lo que A'B' ≅ B'D.
  
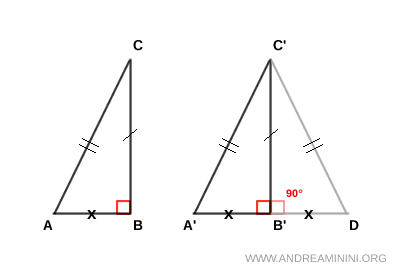
  En consecuencia, los triángulos A'B'C' ≅ B'C'D son congruentes según el tercer criterio de congruencia (LLL), pues sus tres lados son iguales. Dado que ABC ≅ B'C'D y A'B'C' ≅ B'C'D, por la propiedad transitiva se concluye que ABC ≅ A'B'C', como se quería demostrar.

Triángulo Rectángulo y Trigonometría

En trigonometría, el triángulo rectángulo desempeña un papel fundamental.

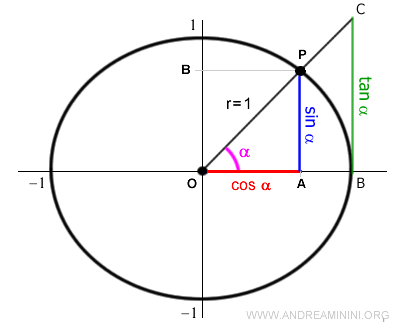
Prácticamente todas las funciones trigonométricas básicas están, de una forma u otra, vinculadas al triángulo rectángulo.

• Seno
  El seno se define como la razón entre el cateto opuesto y la hipotenusa: $$ \sin ( \alpha ) = \frac{AP}{OP} $$
• Coseno
  El coseno se define como la razón entre el cateto adyacente y la hipotenusa: $$ \cos ( \alpha ) = \frac{OA}{OP} $$
• Tangente
  La tangente se define como la razón entre el cateto opuesto y el cateto adyacente: $$ \tan( \alpha) = \frac{AP}{OA} = \frac{\sin( \alpha )}{\cos( \alpha )} $$

Si tomamos uno de los ángulos agudos del triángulo (distinto al recto), los lados del triángulo se pueden relacionar directamente con estas funciones.

La trigonometría posee innumerables aplicaciones prácticas

Por ejemplo, se emplea en navegación para calcular distancias, en arquitectura para diseñar estructuras, en electrónica para analizar ondas, y en muchísimos otros campos.

Así, el triángulo rectángulo es, sin duda, una de las figuras geométricas más relevantes y presentes en nuestra vida cotidiana.

Puntos Clave

Algunas observaciones y datos relevantes sobre los triángulos rectángulos.

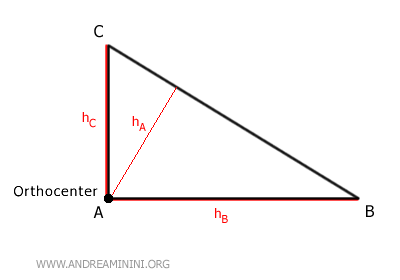
• Ortocentro
  En un triángulo rectángulo, el ortocentro se sitúa exactamente en el vértice del ángulo recto.
  
• En un triángulo rectángulo, los ángulos agudos son complementarios
  
  

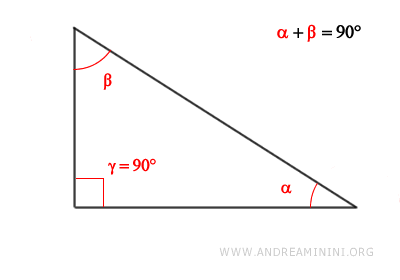
  Demostración: Un triángulo rectángulo posee un ángulo recto (90°). Según el teorema de la suma de los ángulos interiores, la suma de los ángulos de un triángulo siempre es 180°. $$ \alpha + \beta + \gamma = 180° $$ Si uno de los ángulos es recto, por ejemplo γ = 90°, entonces: $$ \alpha + \beta + 90° = 180° $$ $$ \alpha + \beta = 180° - 90° $$ $$ \alpha + \beta = 90° $$ Por lo tanto, los ángulos agudos de un triángulo rectángulo son ángulos complementarios, es decir, su suma equivale a un ángulo recto.

• En un triángulo rectángulo, la mediana correspondiente a la hipotenusa mide exactamente la mitad de ésta
  En cualquier triángulo rectángulo, la longitud de la mediana (AM) trazada hacia la hipotenusa (BC) es exactamente la mitad de la longitud de la hipotenusa: (AM ≅ 1/2 BC)
  
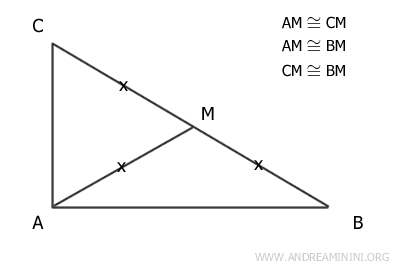
  El recíproco también es cierto: si en un triángulo una mediana mide exactamente la mitad del lado sobre el que se traza, entonces el triángulo es rectángulo.
  

  Demostración: Consideremos un triángulo rectángulo ABC, el punto medio M de la hipotenusa y la mediana trazada hasta dicha hipotenusa. Sabemos que el ángulo α es recto (α=90°) y que los segmentos BM y CM son congruentes, ya que M es el punto medio de la hipotenusa AB.
  
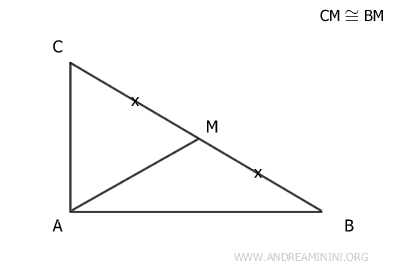
  Prolongamos el segmento AM construyendo un segmento MD congruente a AM. Después unimos los puntos B y D, y C y D, formando un cuadrilátero.
  
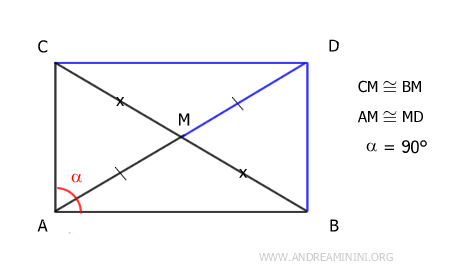
  Dicho cuadrilátero es un paralelogramo porque sus diagonales AD y BC se cortan en su punto medio. Además, dado que el ángulo α es recto (por la hipótesis inicial del triángulo rectángulo), el paralelogramo es en realidad un rectángulo. En un rectángulo, las diagonales son congruentes, es decir, AD ≅ BC. Por tanto, sus mitades también lo son: AD/2 ≅ BC/2, lo cual implica que AM ≅ BM y AM ≅ CM. Esto demuestra que, en un triángulo rectángulo, la mediana trazada hacia la hipotenusa mide exactamente la mitad de ésta.
  
  Demostración Alternativa. Consideremos un triángulo rectángulo y sea M el punto medio de la hipotenusa (AC). Entonces, BM es la mediana trazada hacia la hipotenusa.
  
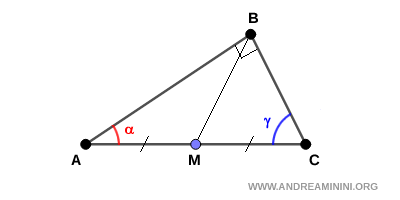
  Ahora prolongamos la mediana BM construyendo un segmento BD de igual longitud a BM. Después unimos el punto D con A, formando el triángulo ABD.
  
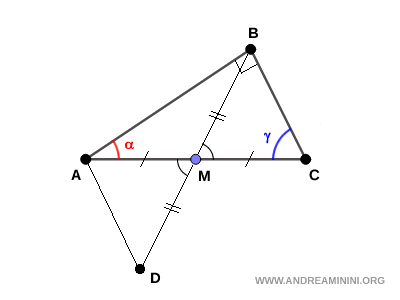
  Los triángulos ADM y BCM son congruentes según el primer criterio de congruencia de triángulos (LAL), pues comparten dos pares de lados congruentes (AM ≅ CM por definición de punto medio, y BD ≅ BM por construcción), y los ángulos comprendidos $ \angle AMD $ y $ \angle BMC $ son congruentes al ser opuestos por el vértice en el punto M. Al ser congruentes, estos triángulos poseen ángulos y lados iguales. En particular, se cumple que $ \alpha' \cong \gamma $.
  
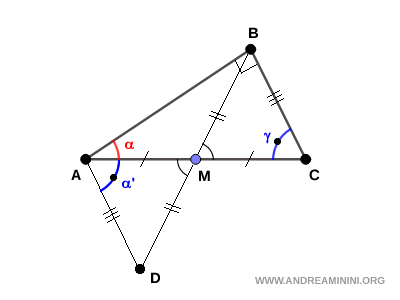
  En el triángulo ABC sabemos que los ángulos $ \alpha $ y $ \gamma $ son complementarios: $$ \alpha + \gamma = 90^\circ $$ Como $ \alpha' \cong \gamma $, se deduce que $ \alpha + \alpha' = 90^\circ $ también. Así, el triángulo ABD es rectángulo. Además, los triángulos ABD y ABC son congruentes porque comparten el lado AB y los otros lados también son congruentes (AD ≅ BC). Por lo tanto, sus hipotenusas son iguales: $$ AC \cong BD $$ Por construcción, sabemos que $ BD = 2 \, BM $, de manera que: $$ AC \cong 2 \, BM $$ De aquí se concluye que la mediana BM mide exactamente la mitad de la hipotenusa AC: $$ BM \cong \frac{1}{2} \, AC $$ como se quería demostrar.
  
  Demostración del Teorema Recíproco. Consideremos un triángulo ABC en el cual la mediana BM mide la mitad del lado AC sobre el que se ha trazado.
  
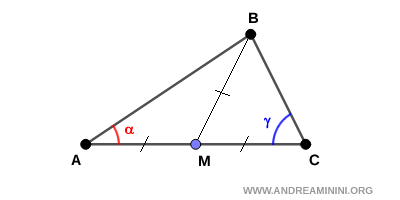
  Es decir: $$ BM = \frac{1}{2} \, AC $$ De esto se deduce que los segmentos BM, AM y CM son congruentes: $$ BM \cong AM \cong CM $$ Como consecuencia, los triángulos ABM y CBM son isósceles, pues cada uno posee dos lados iguales (BM ≅ AM y BM ≅ CM). Por lo tanto, los ángulos en la base de los triángulos ABM y CBM son congruentes.
  
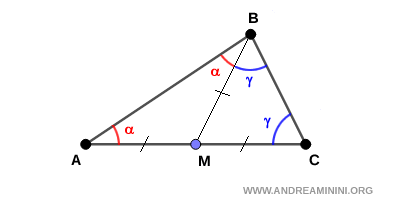
  Como la suma de los ángulos interiores de un triángulo es siempre 180°, los ángulos en el triángulo ABC cumplen: $$ \alpha + \gamma + (\alpha + \gamma) = 180^\circ $$ lo cual se simplifica a: $$ 2\alpha + 2\gamma = 180^\circ $$ Dividiendo entre 2, se obtiene: $$ \alpha + \gamma = 90^\circ $$ Por lo tanto, el ángulo restante en el triángulo ABC es recto. En consecuencia, el triángulo ABC es rectángulo, tal como queríamos demostrar.

• El caso del triángulo rectángulo con ángulos agudos de 30° y 60°
  

  

  
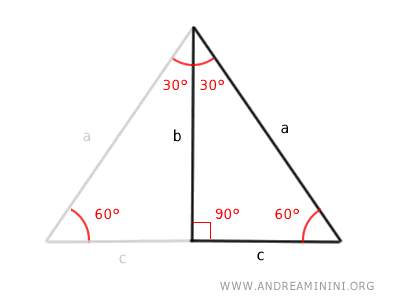
  Un triángulo rectángulo cuyos ángulos agudos miden 30° y 60° corresponde exactamente a la mitad de un triángulo equilátero. Esto permite calcular las longitudes de todos sus lados a partir de uno solo. $$ a = \frac{2b}{\sqrt{3}} $$ $$ b = \frac{a}{2} \sqrt{3} $$ $$ c = \frac{a}{2} $$ Estas fórmulas son exclusivas de los triángulos con ángulos interiores de 30°, 60° y 90°.
• El caso del triángulo rectángulo con dos ángulos agudos de 45° (triángulo rectángulo isósceles)
  

  

  
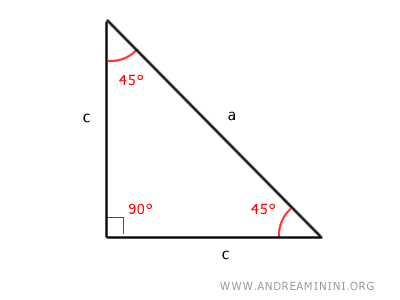
  Este caso particular de triángulo rectángulo es también un triángulo isósceles, pues cuenta con dos catetos de igual longitud. Esto permite calcular las dimensiones de todos sus lados a partir de uno solo. $$ c = \frac{a}{ \sqrt{2} } $$ $$ a = c \cdot \sqrt{2} $$ Estas relaciones son válidas únicamente para triángulos con dos ángulos agudos de 45°.
• Dos triángulos rectángulos son semejantes si sus catetos son proporcionales
  Según el segundo criterio de semejanza de triángulos, dos triángulos son semejantes si sus lados son proporcionales y el ángulo comprendido es congruente.
  
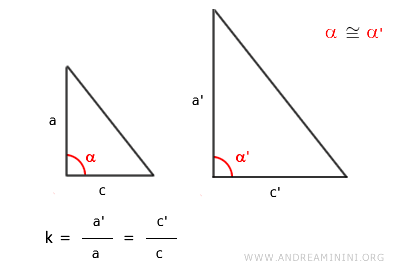
  En los triángulos rectángulos, el ángulo formado entre los catetos siempre es recto (90°) y, por tanto, congruente. Así, si los catetos son proporcionales, según el segundo criterio de semejanza, los dos triángulos son semejantes, es decir, tienen todos sus ángulos iguales y la misma forma, aunque puedan diferir en tamaño u orientación.
• Dos triángulos rectángulos con un ángulo agudo congruente son semejantes
  La suma de los ángulos interiores de un triángulo siempre es 180°. $$ \alpha + \beta + \gamma = 180° $$ Dado que en dos triángulos rectángulos el ángulo recto mide 90°, si además tienen un ángulo agudo congruente, entonces el tercer ángulo también será congruente por diferencia. Por consiguiente, ambos triángulos poseen todos sus ángulos iguales y, según el primer criterio de semejanza de triángulos, son semejantes.
  

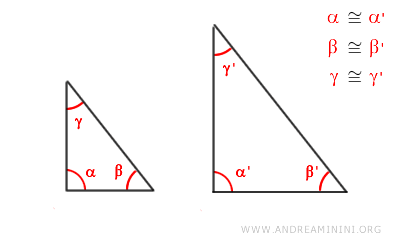
Y así sucesivamente.