Triángulo Escaleno

Se denomina triángulo escaleno a aquel cuyas tres lados tienen longitudes distintas o, dicho de otro modo, cuyos tres ángulos son diferentes entre sí.

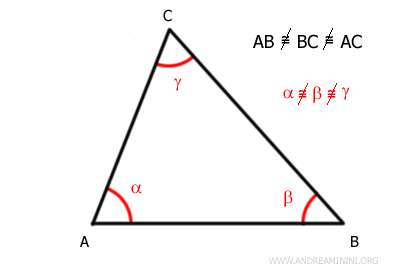
En otras palabras, los lados de un triángulo escaleno siempre tienen medidas desiguales.

Como consecuencia, sus tres ángulos también difieren unos de otros.

Nota: Habitualmente, cuando se habla de "triángulos" sin especificar el tipo, se hace referencia a cualquier clase de triángulo. Los triángulos escalenos representan la forma más general. Por ello, cuando se estudian propiedades generales de los triángulos, suele tomarse como modelo un triángulo escaleno.

Un Ejemplo Práctico

Vamos a analizar el triángulo ABC.

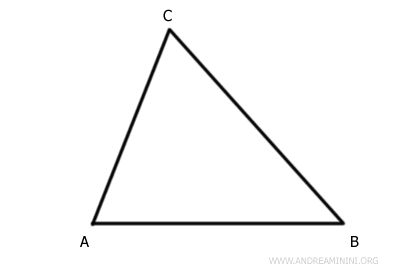
Sus tres lados, AB, BC y AC, no son congruentes, lo que significa que tienen longitudes distintas.

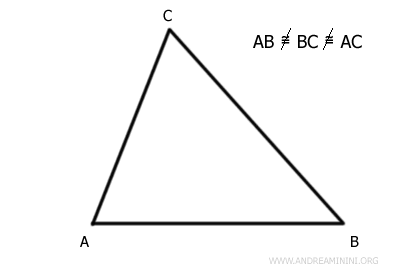
En consecuencia, sus tres ángulos tampoco son congruentes.

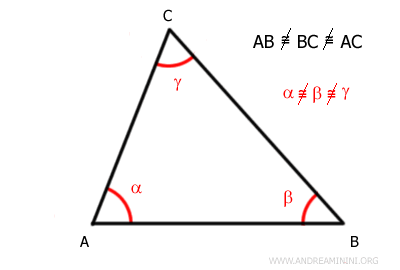
Por lo tanto, podemos concluir que se trata de un triángulo escaleno.

Tipos de Triángulos Escalenos

Existen tres clases de triángulos escalenos:

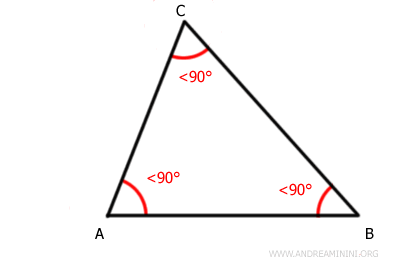
• Triángulo Escaleno Acutángulo
  Presenta tres lados de distinta longitud y tres ángulos diferentes, todos ellos agudos. Es decir, cada uno mide menos de 90°. Se incluye dentro del conjunto de los triángulos acutángulos.
  
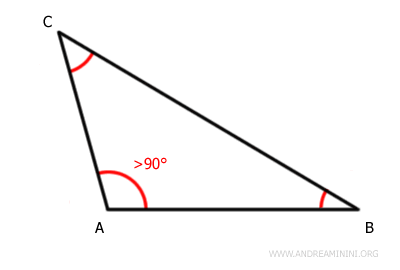
• Triángulo Escaleno Obtusángulo
  Tiene sus tres lados desiguales y tres ángulos diferentes, siendo uno de ellos obtuso, es decir, mayor de 90°. Forma parte del grupo de los triángulos obtusángulos.
  
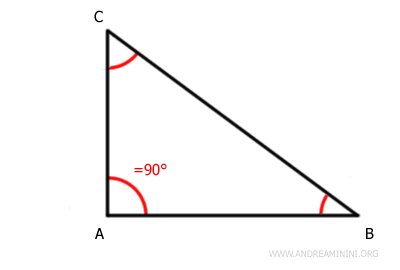
• Triángulo Escaleno Rectángulo
  Posee tres lados de distintas longitudes y tres ángulos diferentes. Además, cuenta con un ángulo recto, que mide exactamente 90°. Pertenece al conjunto de los triángulos rectángulos.
  

Propiedades

Estas son algunas propiedades de los triángulos escalenos, recopiladas en el sitio web de YouMath:

• Convexidad
  Todo triángulo escaleno es, por definición, un polígono convexo.
• Suma de Ángulos Interiores
  La suma de los ángulos interiores de un triángulo escaleno es siempre 180° (π), propiedad común a todos los triángulos en geometría euclidiana.
• Suma de Ángulos Exteriores
  La suma de los ángulos exteriores de cualquier triángulo escaleno es 360° (2π).
• Relación entre Ángulos y Lados
  El lado opuesto al ángulo interior más grande es el lado más largo. De forma análoga, el lado opuesto al ángulo más pequeño es el lado más corto del triángulo.
• Desigualdad Triangular
  La longitud de cualquier lado es siempre inferior a la suma de las longitudes de los otros dos lados.

Estas propiedades se cumplen en cualquier triángulo escaleno, sin importar su clasificación según sus ángulos (acutángulo, obtusángulo o rectángulo).

Y así sucesivamente.