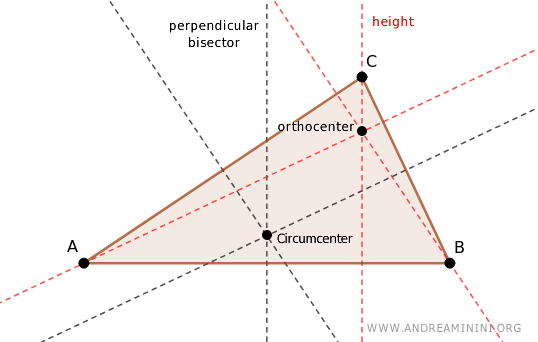
Ortocentro

En un triángulo, el ortocentro es el punto donde se cortan sus tres alturas.

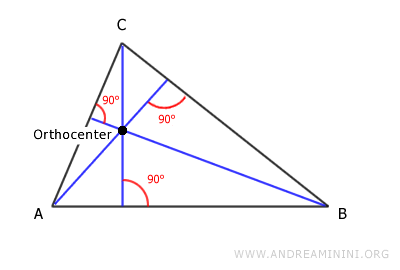
Una altura es una recta perpendicular a uno de los lados del triángulo (o a su prolongación), que pasa por el vértice opuesto.

Todo triángulo posee tres alturas, pues tiene tres vértices y tres lados.

El punto donde estas tres rectas se intersectan se llama ortocentro.

Posición del Ortocentro

La posición del ortocentro depende de la naturaleza de los ángulos del triángulo.

El ortocentro puede encontrarse:

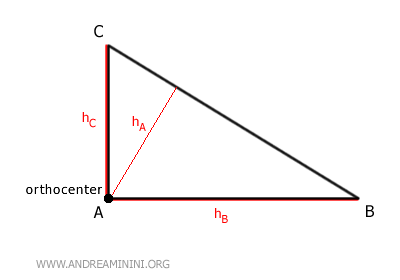
• Dentro del triángulo si este es acutángulo. Si sus tres ángulos son menores de 90°, el ortocentro se halla en el interior del triángulo.
  
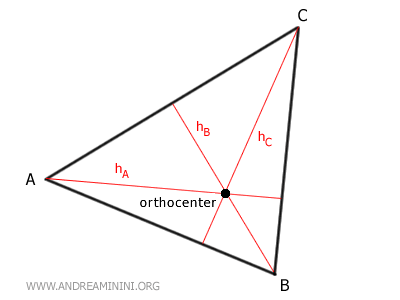
• Fuera del triángulo si se trata de un triángulo obtusángulo. Si uno de sus ángulos es mayor de 90°, el ortocentro se encuentra en el exterior del triángulo.
  
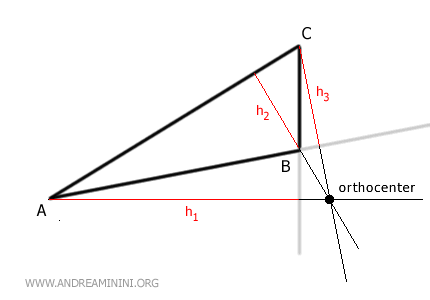
• En uno de los vértices si es un triángulo rectángulo. En este caso, el ortocentro coincide con el vértice en el que se forma el ángulo recto (90°).
  

Demostración

Para demostrar que las alturas concurren en un mismo punto, consideremos el triángulo ABC.

Se trazan rectas paralelas a los lados del triángulo que pasan por el vértice opuesto.

Estas rectas paralelas se intersectan en los puntos D, E y F.

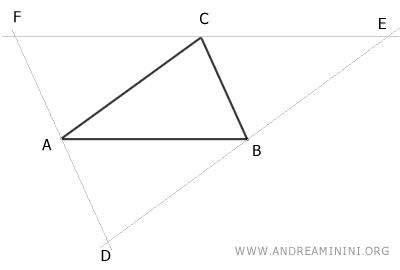
De esta construcción se deduce que:

• Los segmentos AD||BC y AC||DB son paralelos, formando el paralelogramo ADBC.
• Los segmentos AF||BC y AB||CF son paralelos, formando el paralelogramo ABCF.

Como paralelogramos, presentan lados opuestos congruentes: AD≅BC, AB≅DB, AF≅BC y AB≅CF.

Por la propiedad transitiva, dado que AD≅BC y AF≅BC, se concluye que AD≅AF.

$$ \overline{AD} \cong \overline{AF} $$

Por lo tanto, el punto A es el punto medio del lado DF.

Seguidamente, se traza la altura AG del triángulo ABC, perpendicular al lado BC y que pasa por el vértice A.

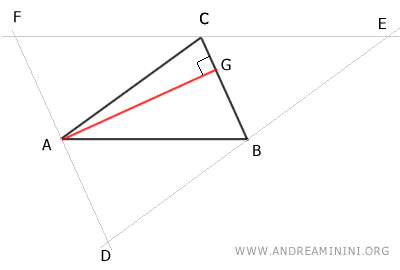
La recta que contiene el segmento AG es también perpendicular al lado DF, ya que DF es paralelo a BC por construcción.

Por tanto, la recta que contiene el segmento AG (altura del triángulo ABC) es un eje del triángulo DEF, pues es perpendicular al lado DF y pasa por su punto medio A.

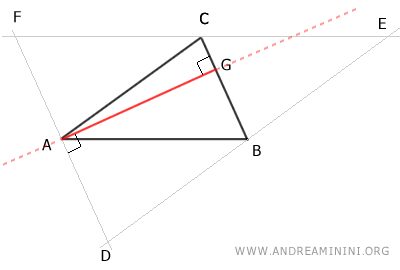
De manera similar, se puede demostrar que el punto B es el punto medio del segmento DE.

Por construcción, existen dos paralelogramos, ADBC y ABEC, cuyos lados opuestos son congruentes.

Por la propiedad transitiva, si DB≅AC y BE≅AC, se concluye que DB≅BE.

$$ \overline{DB} \cong \overline{BE} $$

Por lo tanto, el punto B es el punto medio del segmento DE.

Después, se traza la altura BH del triángulo ABC, perpendicular al lado AC y que pasa por el vértice B.

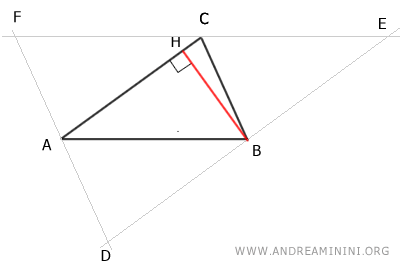
Como AC||DE son paralelos por construcción, la recta que contiene el segmento BH es también perpendicular al lado DE.

Así, la altura BH del triángulo ABC coincide con el eje del lado DE del triángulo DEF.

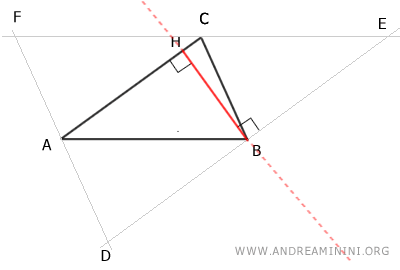
Finalmente, aplicando el mismo razonamiento, se demuestra que el punto C es el punto medio del segmento EF.

Por construcción, existen dos paralelogramos, ABCF y ABEC, con lados opuestos congruentes.

Por la propiedad transitiva, si AB≅CF y AB≅CE, se deduce que CF≅CE.

$$ \overline{CF} \cong \overline{CE} $$

Por lo tanto, si CF≅CE, el punto C es el punto medio del segmento EF.

Se traza entonces la altura IC del triángulo ABC, perpendicular al lado AB y que pasa por el vértice C.

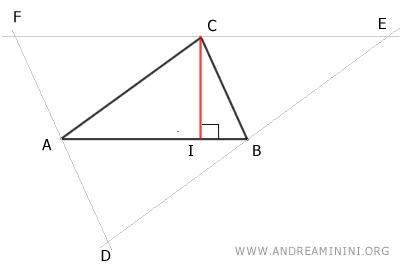
Como AB||EF son paralelos por construcción, se deduce que la recta que contiene el segmento IC también es perpendicular al lado EF.

Por tanto, la altura IC del triángulo ABC coincide con el eje del lado EF del triángulo DEF.

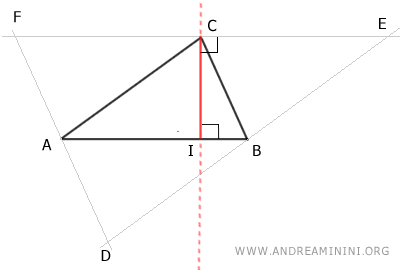
Hasta aquí, hemos demostrado que las alturas del triángulo ABC son segmentos contenidos en los ejes del triángulo DEF.

En conclusión, sabiendo que los ejes de un triángulo siempre concurren en un único punto (véase la demostración del circuncentro), se deduce que las rectas que contienen las alturas de un triángulo se intersectan en un punto común.

En otras palabras, las rectas que definen las alturas de un triángulo son paralelas a los ejes de ese mismo triángulo, pues ambas son perpendiculares a los mismos lados.

Rectas paralelas a rectas concurrentes también son concurrentes.

Por lo tanto, una vez demostrado que los ejes de un triángulo se cortan en un único punto (circuncentro), se concluye que las rectas que contienen las alturas del triángulo se intersectan en un único punto, denominado ortocentro.

Y así sucesivamente.