La suma de dos ángulos interiores de un triángulo
En todo triángulo, la suma de cualquier par de ángulos interiores es siempre menor que 180°.
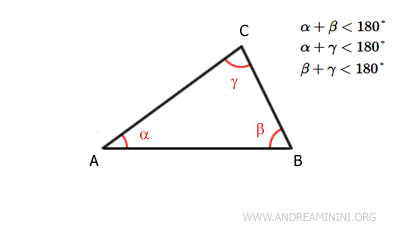
Por ejemplo, en un triángulo cualquiera ABC:
Se verifican las siguientes desigualdades:
$$ \alpha + \beta < 180^\circ \\ \alpha + \gamma < 180^\circ \\ \beta + \gamma < 180^\circ $$
De este teorema se deduce un resultado fundamental:
Todo triángulo posee al menos dos ángulos agudos (es decir, menores de 90°).
En otras palabras, ningún triángulo puede tener más de un ángulo recto u obtuso, ya que en tal caso la suma de dos de sus ángulos superaría los 180°, lo cual contradice las propiedades básicas de la geometría euclídea.
Demostración
Consideremos un triángulo cualquiera ABC:
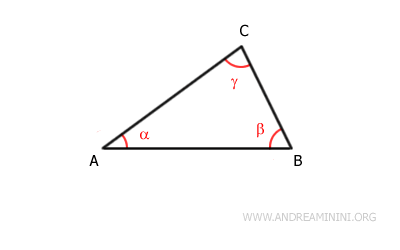
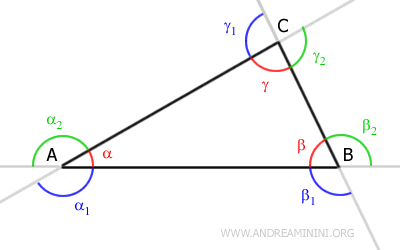
El triángulo tiene tres ángulos interiores (α, β, γ), y cada uno de ellos está asociado a dos ángulos exteriores adyacentes.
Por ejemplo, el ángulo interior β está adyacente a los ángulos exteriores βe y βe'.
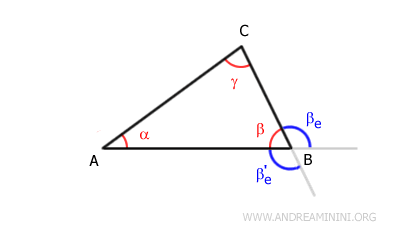
Tomemos el ángulo exterior βe:
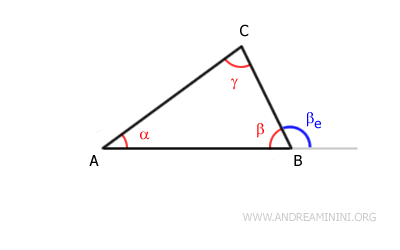
Según el teorema del ángulo exterior, dicho ángulo es mayor que cada uno de los ángulos interiores que no son adyacentes a él.
En este caso, se cumple que:
$$ \beta_e > \alpha \quad \text{y} \quad \beta_e > \gamma $$
Esto significa que βe es mayor que los ángulos interiores opuestos (α y γ), pero no se compara con β, ya que ambos son adyacentes y forman un ángulo llano.
Partamos de la primera desigualdad:
$$ \beta_e > \alpha $$
Si sumamos el ángulo β a ambos miembros:
$$ \beta_e + \beta > \alpha + \beta $$
Sabemos que la suma de un ángulo interior y su adyacente exterior siempre da lugar a un ángulo llano, es decir:
$$ \beta_e + \beta = 180^\circ $$
Por tanto:
$$ 180^\circ > \alpha + \beta $$
Hemos demostrado que la suma de los ángulos α y β es menor que 180°:
$$ \alpha + \beta < 180^\circ $$
Repitiendo el razonamiento con los otros ángulos exteriores se obtiene el mismo resultado para las demás combinaciones posibles de ángulos del triángulo.
Lo cual completa la demostración.