Teorema del ángulo exterior en los triángulos

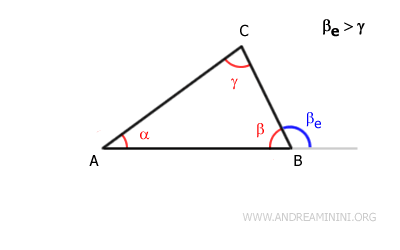
En todo triángulo, un ángulo exterior ($ \beta_e $) es mayor que cualquiera de los ángulos interiores no adyacentes ($ \alpha $ y $ \gamma $).

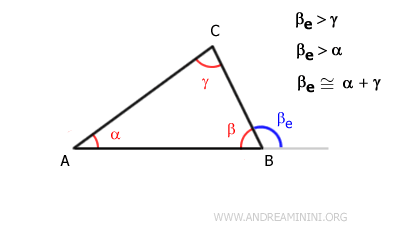
Esto se debe a que todo ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores no adyacentes:
$$ \beta_e = \alpha + \gamma $$

Se trata de un teorema general, válido para cualquier triángulo.

Por ejemplo, en el triángulo ABC, el ángulo exterior en el vértice B, $ \beta_e $, es mayor que los ángulos interiores $ \alpha $ y $ \gamma $.

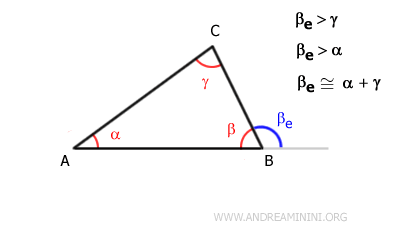
Por tanto, en el triángulo ABC, el ángulo exterior $ \beta_e $ es mayor que cualquier ángulo interior distinto de $ \beta $.

Demostración

Consideremos el triángulo ABC.

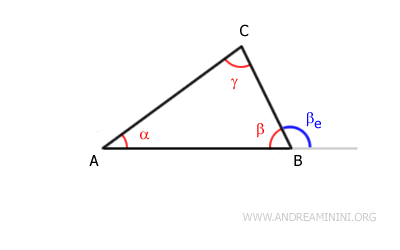
Prolongamos el lado $ AB $ más allá del punto $ B $, generando el ángulo exterior $ \beta_e $, suplementario al ángulo interior $ \beta $.

A continuación, trazamos el segmento $ BE $, paralelo al lado $ AC $, que pasa por el vértice $ B $.

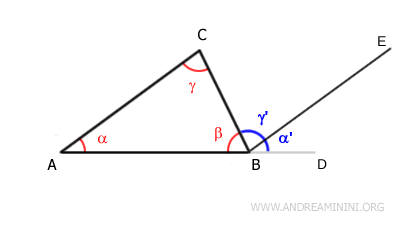
Por construcción, el ángulo exterior $ \beta_e $ es la suma de los ángulos $ \alpha' $ y $ \gamma' $:

$$ \beta_e = \alpha' + \gamma' $$

Según el teorema de las paralelas, al ser $ BE $ y $ AC $ paralelas y estar cortadas por la transversal $ CB $, los ángulos alternos internos son congruentes:

$$ \gamma = \gamma' $$

De igual modo, las mismas paralelas $ BE $ y $ AC $, cortadas ahora por la transversal $ AB $, generan ángulos correspondientes congruentes:

$$ \alpha = \alpha' $$

Nota: Hemos aplicado dos veces el teorema de las paralelas sobre las mismas rectas $ BE $ y $ AC $, empleando transversales distintas: primero $ CB $ y luego $ AB $.

De ello se deduce que el ángulo exterior $ \beta_e $ es igual a la suma de los dos ángulos interiores no adyacentes:

$$ \beta_e = \alpha + \gamma $$

Por consiguiente, como:

$$ \beta_e = \alpha + \gamma $$

se sigue que el ángulo exterior $ \beta_e $ es necesariamente mayor que cada uno de los dos ángulos interiores por separado:

$$ \beta_e > \alpha $$

$$ \beta_e > \gamma $$

Así queda demostrado que el ángulo exterior es mayor que cualquiera de los ángulos interiores no adyacentes, y que su medida es exactamente igual a la suma de ambos.

Demostración alternativa

A] El ángulo exterior es mayor que los ángulos interiores no adyacentes

Consideremos un triángulo cualquiera ABC.

Analicemos el ángulo exterior en el vértice B, que denominaremos en adelante $ \beta_e $.

Debemos demostrar que el ángulo exterior $ \beta_e $ es mayor que los ángulos interiores no adyacentes $ \alpha $ y $ \gamma $.

Primera parte

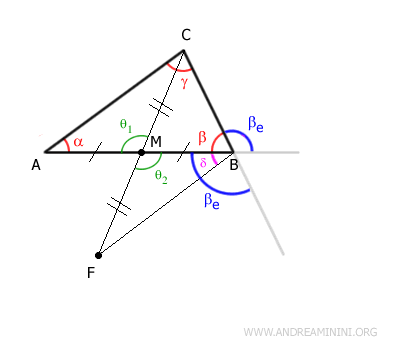
Identificamos el punto medio M del lado $ BC $, adyacente al ángulo $ \beta $, y trazamos la mediana $ AM $.

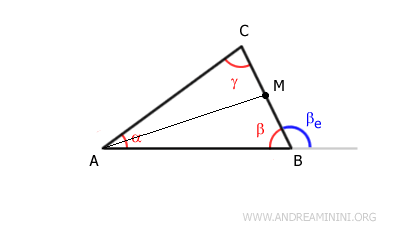
De este modo obtenemos dos segmentos congruentes:

$$ BM \cong CM $$

Extendemos el segmento $ AM $ añadiendo un nuevo segmento $ ME $ tal que $ AM = ME $, duplicando así su longitud.

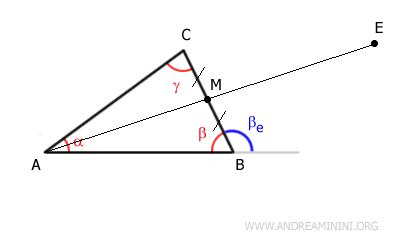
En resumen:

$$ BM \cong CM $$

$$ AM \cong ME $$

A continuación, unimos los puntos $ B $ y $ E $ mediante el segmento $ BE $.

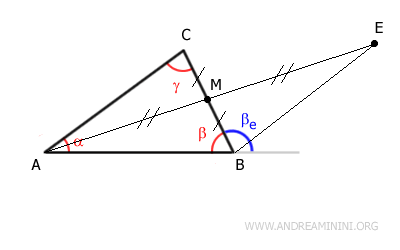
En el punto M, los segmentos se cruzan formando dos ángulos opuestos por el vértice, congruentes:

$$ \theta_1 \cong \theta_2 $$

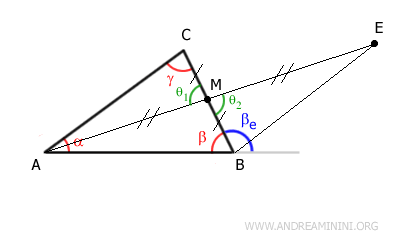
Por tanto, de acuerdo con el primer criterio de congruencia, los triángulos $ AMC $ y $ BME $ son congruentes, ya que tienen dos lados congruentes $ BM \cong CM $, $ AM \cong ME $, y el ángulo comprendido también congruente $ \theta_1 \cong \theta_2 $.

$$ AMC \cong BME $$

Por consiguiente, los triángulos $ AMC $ y $ BME $ tienen lados y ángulos congruentes, en el mismo orden.

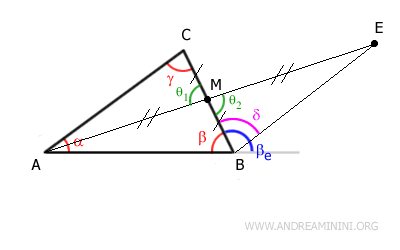
Observamos que:

$$ \gamma \cong \delta $$

Además, el ángulo $ \delta $ es menor que el ángulo exterior $ \beta_e $, puesto que el segmento $ BE $ divide a $ \beta_e $ en dos partes:

$$ \delta < \beta_e $$

Como $ \gamma \cong \delta $, se deduce que:

$$ \gamma < \beta_e $$

Por tanto, el ángulo exterior $ \beta_e $ es mayor que el ángulo interior $ \gamma $.

Segunda parte

Ahora repetimos un razonamiento análogo para demostrar que $ \beta_e $ también es mayor que $ \alpha $.

Identificamos el punto medio M del lado $ AB $, adyacente a $ \beta $, y trazamos la mediana $ CM $.

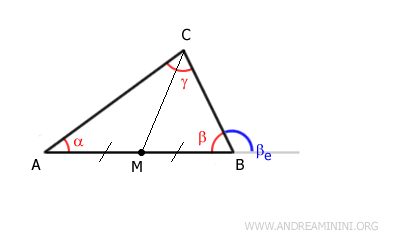
Los segmentos:

$$ \overline{AM} \cong \overline{BM} $$

Extendemos el segmento $ CM $ añadiendo el segmento $ MF $ de igual longitud:

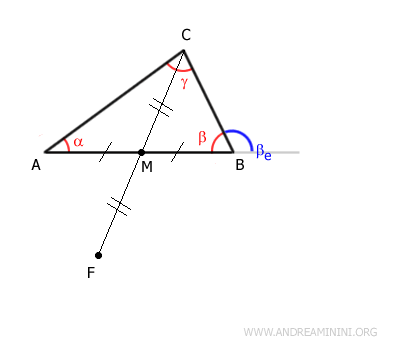
Por tanto:

$$ \overline{CM} \cong \overline{MF} $$

En resumen:

$$ \overline{AM} \cong \overline{BM} $$

$$ \overline{CM} \cong \overline{MF} $$

Ahora unimos los puntos $ B $ y $ F $ con el segmento $ BF $.

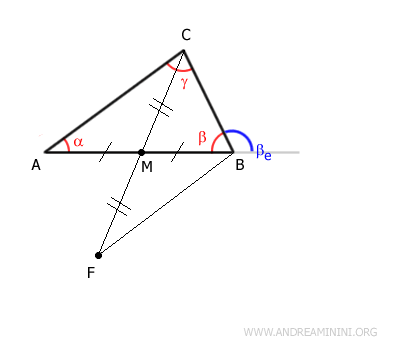
En M, los segmentos $ AB $ y $ CF $ se cruzan formando dos ángulos opuestos por el vértice:

$$ \theta_1 \cong \theta_2 $$

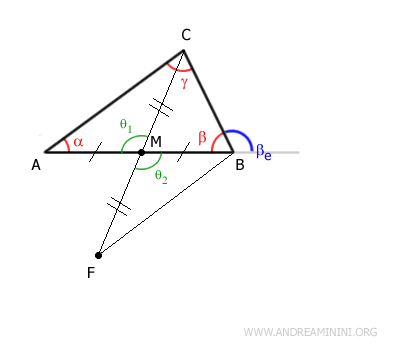
Por el primer criterio de congruencia, los triángulos $ AMC $ y $ BMF $ son congruentes:

$$ AMC \cong BMF $$

En consecuencia:

$$ \alpha \cong \delta $$

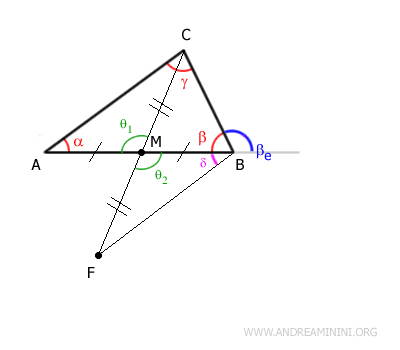
Prolongamos el lado $ BC $ para comparar $ \beta_e $ con $ \delta $. Al ser ángulos opuestos por el vértice, proyectamos un ángulo congruente a $ \beta_e $:

Se aprecia claramente que:

$$ \delta < \beta_e $$

Siendo $ \delta \cong \alpha $, se concluye que:

El ángulo exterior $ \beta_e $ es mayor que el ángulo interior $ \alpha $.

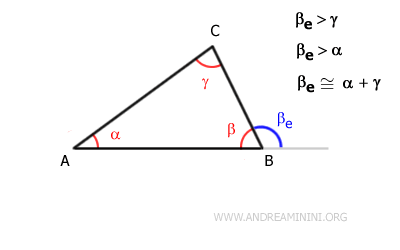
Conclusión

En un triángulo, el ángulo exterior $ \beta_e $ es mayor que los ángulos interiores no adyacentes $ \alpha $ y $ \gamma $.

Queda así demostrado el teorema del ángulo exterior para los triángulos.

B] El ángulo exterior es igual a la suma de los ángulos interiores no adyacentes

Vamos a demostrar ahora que el ángulo exterior es igual a la suma de los dos ángulos interiores no adyacentes.

Consideremos el triángulo ABC y su ángulo exterior $ \beta_e $.

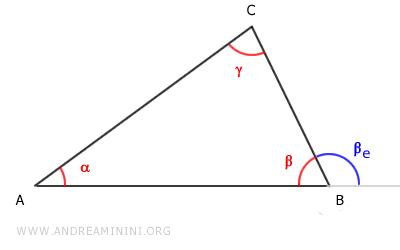
Trazamos las rectas que contienen los lados del triángulo y las denominamos a, b y c:

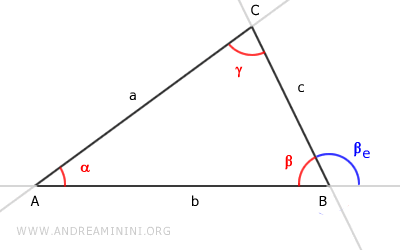
Trazamos ahora una recta d, paralela al lado $ AC $, que pasa por el vértice $ B $.

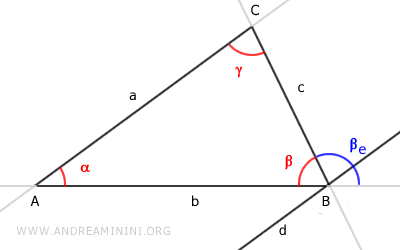
De este modo, podemos descomponer el ángulo exterior como la suma de dos ángulos:
$ \beta_e = \beta'_e + \beta''_e $

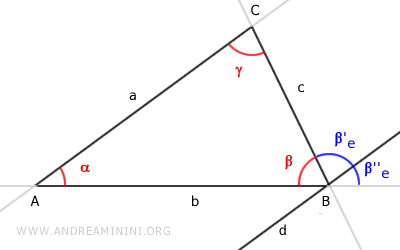
El ángulo $ \beta'_e $ es un ángulo alterno interno entre las paralelas a || d, cortadas por la transversal c.

Por el teorema de las paralelas, los ángulos alternos internos $ \gamma $ y $ \beta'_e $ son congruentes:
$ \gamma \cong \beta'_e $.

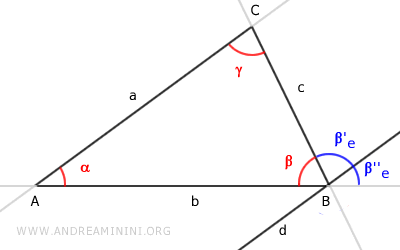
El ángulo $ \beta''_e $ es un ángulo correspondiente entre las paralelas a || d, cortadas por la transversal b.

Por el mismo teorema, los ángulos correspondientes $ \alpha $ y $ \beta''_e $ son congruentes:
$ \alpha \cong \beta''_e $.

Como el ángulo exterior es la suma:
$ \beta_e = \beta'_e + \beta''_e $, y sabemos que:
$ \gamma \cong \beta'_e $ y $ \alpha \cong \beta''_e $, se deduce:

$$ \begin{cases} \beta_e \cong \beta'_e + \beta''_e \\ \\ \gamma \cong \beta'_e \\ \\ \alpha \cong \beta''_e \end{cases} $$

Por tanto:

$$ \beta_e \cong \gamma + \alpha $$

Es decir:
El ángulo exterior $ \beta_e $ es igual a la suma de los ángulos interiores no adyacentes del triángulo.

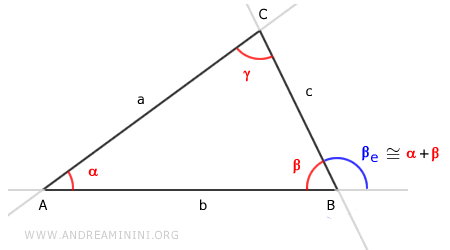
Observaciones

A continuación, algunas observaciones y corolarios que se derivan de este teorema:

• La suma de los ángulos interiores de un triángulo es 180°
  La suma de los ángulos interiores de cualquier triángulo es siempre 180°, es decir, un ángulo llano. Se trata de un invariante geométrico, independiente del tipo o de la forma del triángulo.
  

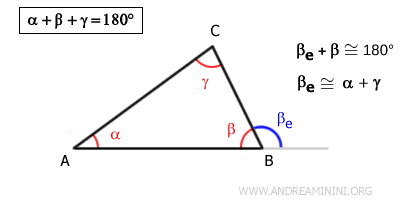
  Demostración. Cada ángulo interior y su correspondiente ángulo exterior suman 180°. Por ejemplo:
  $$ \beta + \beta' = 180° $$
  Además, sabemos que:
  $$ \beta' = \alpha + \gamma $$
  Por tanto:
  $$ \beta + (\alpha + \gamma) = 180° $$
  $$ \alpha + \beta + \gamma = 180° $$

• La suma de dos ángulos interiores es siempre menor que 180°
  Es un corolario inmediato del teorema del ángulo exterior: dado que el ángulo exterior es mayor que cualquiera de los ángulos interiores no adyacentes:
  $$ \alpha + \gamma < 180° $$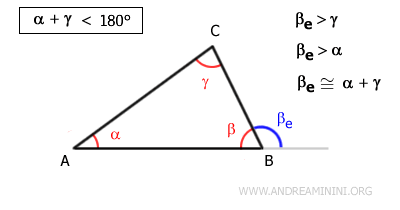

  

  Demostración. Como:
  $$ \beta_e > \gamma $$
  Si sumamos $ \beta $ en ambos miembros:
  $$ \gamma + \beta < \beta_e + \beta $$
  Y como:
  $$ \beta + \beta_e = 180° $$
  Entonces:
  $$ \gamma + \beta < 180° $$
  De modo análogo, se obtiene:
  $$ \alpha + \gamma < 180° $$
  $$ \alpha + \beta < 180° $$

• Un triángulo solo puede tener un ángulo recto o un ángulo obtuso
  Esto se deduce directamente del hecho de que la suma de los tres ángulos es siempre 180°.

  Nota. Si un triángulo tuviera dos ángulos rectos (90° + 90°), no quedaría ángulo para completar 180°. Igualmente, si tuviera dos ángulos obtusos (ambos mayores de 90°), su suma excedería 180°, lo cual es imposible. Por tanto, un triángulo solo puede tener un ángulo recto o un ángulo obtuso, y los otros dos deberán ser agudos.

• Otros corolarios útiles
  A partir del teorema del ángulo exterior se derivan otros resultados interesantes:
  • En un triángulo rectángulo, los dos ángulos agudos son complementarios
    Si uno de los ángulos es recto (90°), los otros dos deben sumar 90°.
  • En un triángulo equilátero, cada ángulo interior mide 60°
    Dado que los tres ángulos suman 180° y son iguales, cada uno mide 60°.
  • Si dos triángulos tienen dos ángulos congruentes, el tercero también lo será
    Como la suma de los tres siempre es 180°:

    Nota. Este resultado es la base del criterio generalizado ASA:
    Si dos triángulos tienen:
    $$ \alpha \cong \alpha' \quad \text{y} \quad \beta \cong \beta' $$
    y un lado congruente:
    $$ BC \cong B'C' $$
    en la misma posición relativa, entonces:
    $$ ABC \cong A'B'C' $$
    aunque los ángulos no sean adyacentes al lado dado, ya que:
    $$ \gamma \cong \gamma' $$
    completará la congruencia.
    

Y así sucesivamente.