Teorema de Pitágoras

El teorema de Pitágoras se aplica a los triángulos rectángulos, es decir, aquellos que poseen un ángulo de 90 grados. Su enunciado clásico afirma:

En un triángulo rectángulo, el área del cuadrado construido sobre la hipotenusa (el lado opuesto al ángulo recto) es igual a la suma de las áreas de los cuadrados construidos sobre los catetos. $$ a^2 + b^2 = c^2 $$ Donde "c" representa la hipotenusa y "a" y "b" los catetos.

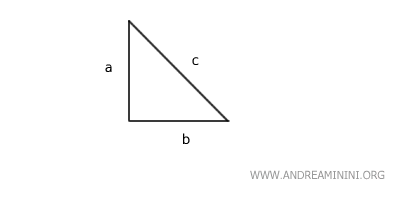
Este célebre teorema lleva el nombre del matemático griego Pitágoras, a quien se atribuye tradicionalmente su formulación.

Utilidad

El teorema permite calcular la longitud de los lados de un triángulo rectángulo.

Conociendo dos de los lados, es posible determinar el tercero.

Aplicaciones. El teorema de Pitágoras se emplea ampliamente en matemáticas, geometría y física. Resulta fundamental para calcular distancias en el espacio y constituye la base de las funciones trigonométricas: seno, coseno y tangente.

Aunque enunciado hace más de dos milenios, sigue siendo un pilar de la ciencia moderna, presente en numerosas demostraciones y aplicaciones.

Ejemplo práctico

Consideremos un triángulo rectángulo cuyos catetos miden:

$$ a = 4 \quad b = 3 $$

Queremos hallar la hipotenusa "c".

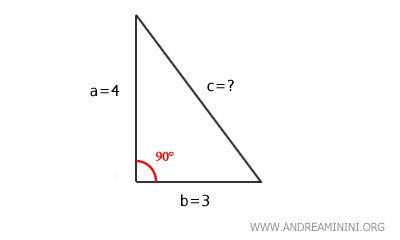
Según el teorema de Pitágoras:

$$ c^2 = a^2 + b^2 $$

Sustituyendo los valores conocidos:

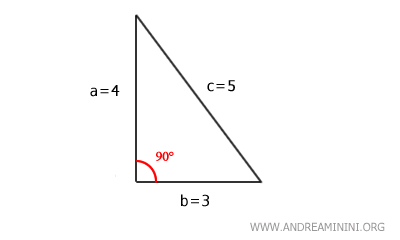
$$ c^2 = 4^2 + 3^2 = 16 + 9 = 25 $$

Extrayendo la raíz cuadrada:

$$ c = \sqrt{25} = 5 $$

Por tanto, la hipotenusa mide 5 unidades.

De igual modo, si conocemos un cateto y la hipotenusa, podemos hallar el otro cateto: $$ a^2 = c^2 - b^2 \qquad b^2 = c^2 - a^2 $$ Basta despejar en la fórmula principal $$ c^2 = a^2 + b^2 $$ para obtener el valor deseado.

Demostraciones

Existen numerosas demostraciones del teorema de Pitágoras, algunas de las cuales se remontan a la Antigüedad.

Una de las más elegantes es de carácter geométrico.

Consideremos un triángulo rectángulo:

Construimos un cuadrado sobre cada uno de sus lados:

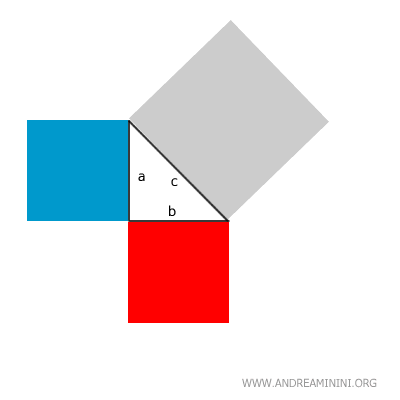
El cuadrado mayor (gris) corresponde a la hipotenusa; los otros dos (rojo y azul), a los catetos.

Dividimos los cuadrados pequeños en triángulos rectángulos:

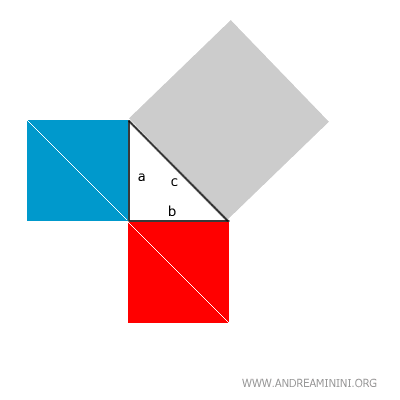
Al reorganizar estas piezas, rellenamos exactamente el área del cuadrado mayor:

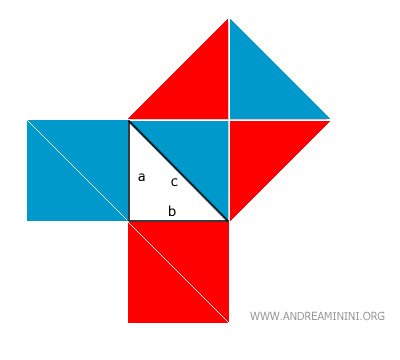
Así queda demostrada visualmente la validez del teorema.

Otra demostración

Otra prueba clásica se basa en un principio de Euclides.

Construimos cuadrados sobre cada lado del triángulo:

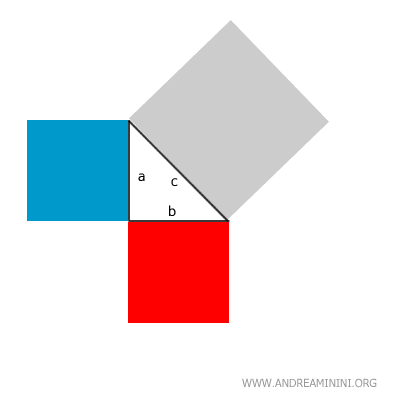
Se traza la altura (h) del triángulo sobre la hipotenusa:

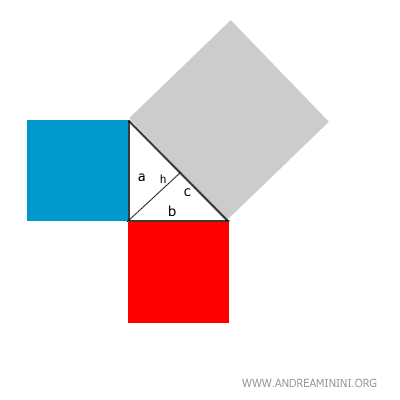
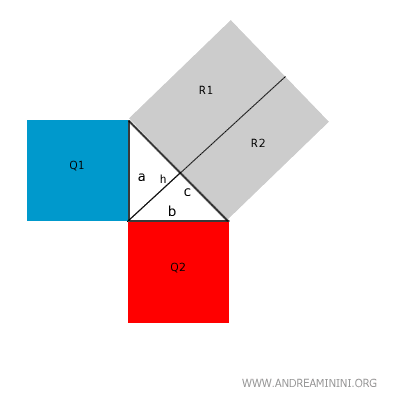
Esta altura divide el cuadrado de la hipotenusa en dos regiones (R1 y R2).

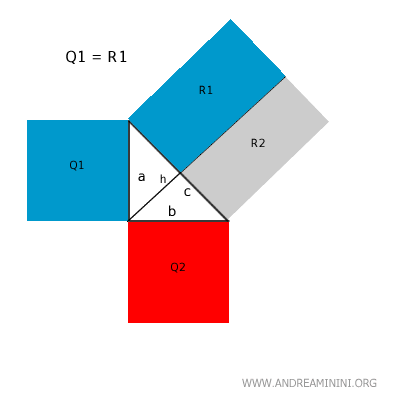
Según el primer teorema de Euclides, el área del rectángulo generado por la proyección del cateto "a" sobre la hipotenusa equivale al cuadrado de dicho cateto: Q1 = R1.

De modo análogo, Q2 = R2 para el cateto "b".

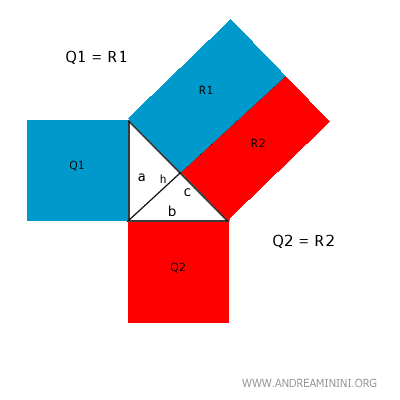
Así se concluye que:

$$ R1 + R2 = Q1 + Q2 $$

lo cual confirma de nuevo el teorema de Pitágoras.

Nota: Existen decenas de demostraciones del teorema; aquí solo hemos mostrado dos de las más célebres.

Observaciones

• Recíproco del teorema de Pitágoras
  

  Si en un triángulo la suma de los cuadrados de dos lados es igual al cuadrado del tercero, entonces el triángulo es rectángulo.

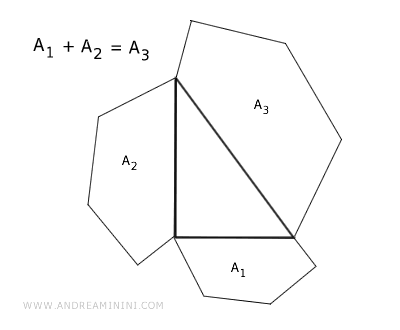
• Teorema de Pitágoras generalizado 

  En un triángulo rectángulo, si se construyen tres polígonos semejantes sobre sus lados, el área del polígono sobre la hipotenusa (A₃) es igual a la suma de las áreas de los otros dos polígonos (A₁ + A₂).
  

• Origen histórico
  Según la leyenda, Pitágoras habría concebido su teorema observando el pavimento de un palacio en Samos: un azulejo fracturado en diagonal revelaba dos triángulos isósceles, y al imaginar un cuadrado sobre la diagonal, dedujo que su área coincidía con la suma de los cuadrados sobre los otros dos lados. Un hermoso ejemplo de cómo una simple observación cotidiana puede inspirar un gran descubrimiento matemático.
• Ternas pitagóricas
  Una terna pitagórica es un conjunto de tres números enteros positivos (a, b, c) que satisfacen la ecuación: $$ a^2 + b^2 = c^2 $$

Y así sucesivamente.