Teorema pitagórico generalizado

En cualquier triángulo rectángulo, si se construyen tres polígonos semejantes sobre sus lados, el área del polígono trazado sobre la hipotenusa es igual a la suma de las áreas de los polígonos construidos sobre los catetos.

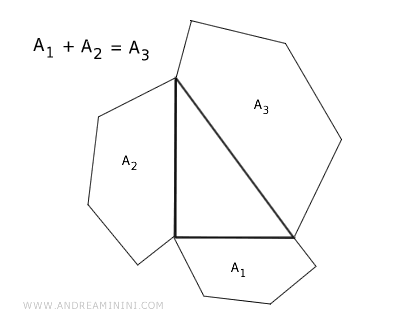
En otras palabras, el área del polígono sobre la hipotenusa equivale a la suma de las áreas de los polígonos sobre los catetos.

Este teorema amplía la idea fundamental del teorema de Pitágoras, mostrando que la relación entre los lados de un triángulo rectángulo no se limita a los cuadrados, sino que se extiende a cualquier figura geométrica semejante construida sobre dichos lados.

Nota: Esto implica que, independientemente de que se construyan triángulos, círculos, polígonos regulares o cualquier otra figura semejante sobre los lados de un triángulo rectángulo, la suma de las áreas de las figuras en los catetos siempre será igual al área de la figura correspondiente en la hipotenusa.

Ejemplo ilustrativo

Consideremos un triángulo rectángulo ABC, sobre cuyos lados se han construido tres pentágonos regulares.

Los catetos AB y AC miden, respectivamente, 4 y 3 unidades, mientras que la hipotenusa BC tiene una longitud de 5 unidades.

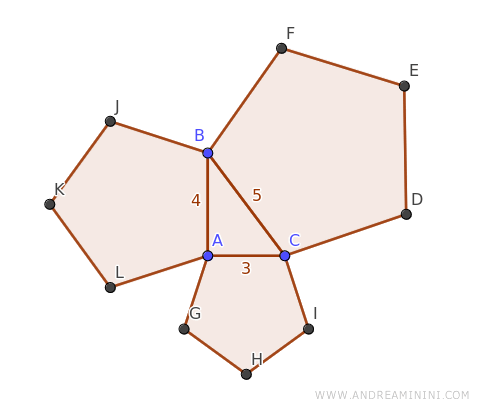
Dado que los pentágonos son polígonos regulares con el mismo número de lados, se consideran polígonos semejantes.

Nota: El teorema no exige que los polígonos sean regulares; basta con que sean semejantes. En este caso se han escogido polígonos regulares por la simplicidad de los cálculos, ya que cualquier par de polígonos regulares con el mismo número de lados son necesariamente semejantes.

Veamos ahora cómo calcular el área de cada pentágono.

El área de un polígono regular se obtiene multiplicando su semiperímetro (p) por el apotema (a):

$$ A = p \cdot a $$

En el caso del pentágono, el apotema (a) es el producto de la longitud del lado (l) por una constante (f), que para los pentágonos es aproximadamente 0.688.

$$ A = p \cdot ( l \cdot f ) $$

$$ A = p \cdot ( l \cdot 0.688 ) $$

Así, obtenemos:

• Área del pentágono sobre el cateto AB (largo 3): $$ A_1 = \frac{3 \cdot 5}{2} \cdot ( 3 \cdot 0.688 ) = 15.48 $$ unidades cuadradas.
• Área del pentágono sobre el cateto AC (largo 4): $$ A_2 = \frac{4 \cdot 5}{2} \cdot ( 4 \cdot 0.688 ) = 27.52 $$ unidades cuadradas.
• Área del pentágono sobre la hipotenusa BC (largo 5): $$ A_3 = \frac{5 \cdot 5}{2} \cdot ( 5 \cdot 0.688 ) = 43 $$ unidades cuadradas.

Una comprobación con Geogebra confirma la exactitud de estos resultados:

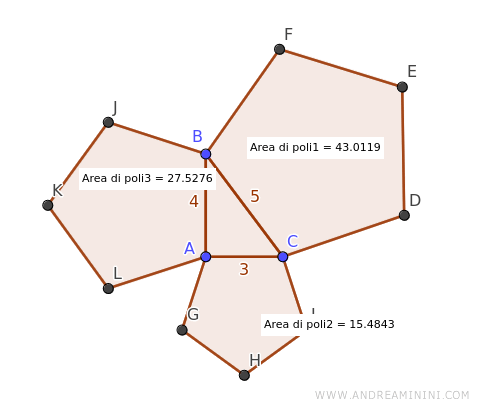
Como corresponde, la suma de las áreas de los polígonos en los catetos es igual al área del polígono en la hipotenusa:

$$ A_1 + A_2 = A_3 $$

$$ 15.48 + 27.52 = 43 $$

$$ 43 = 43 $$

La igualdad se verifica perfectamente.

Demostración

Consideremos de nuevo el triángulo rectángulo con tres polígonos semejantes construidos sobre sus lados.

Según el teorema de las áreas de polígonos semejantes, el área de estos polígonos es proporcional al cuadrado del lado sobre el que se apoyan:

$$ \frac{A_3}{A_2} = \left( \frac{c}{b} \right)^2 $$

Por tanto:

$$ A_3 = A_2 \cdot \left( \frac{c}{b} \right)^2 $$

Sabemos por el teorema de Pitágoras que:

$$ c^2 = a^2 + b^2 $$

Si expresamos $$ a = k \cdot b $$, entonces:

$$ c^2 = (k b)^2 + b^2 = b^2 (k^2 + 1) $$

Y por tanto:

$$ A_3 = A_2 \cdot \frac{b^2 (k^2 + 1)}{b^2} $$

$$ A_3 = A_2 (k^2 + 1) $$

Por otro lado, también se cumple que:

$$ k^2 = \frac{A_1}{A_2} $$

Es decir:

$$ A_1 = k^2 \cdot A_2 $$

Entonces:

$$ A_1 + A_2 = (k^2 \cdot A_2) + A_2 = A_2 (k^2 + 1) $$

Concluyendo que:

$$ A_1 + A_2 = A_3 $$

Hemos demostrado así que la suma de las áreas de los polígonos semejantes sobre los catetos es igual al área del polígono semejante sobre la hipotenusa.

Otra demostración

Partimos de nuevo del triángulo rectángulo ABC con tres polígonos semejantes:

Según el teorema de las áreas de polígonos semejantes:

$$ \frac{A_1}{A_2} = \frac{a^2}{b^2} $$

y

$$ \frac{A_3}{A_2} = \frac{c^2}{b^2} $$

Aplicando la propiedad de composición de razones:

$$ \frac{A_1 + A_2}{A_2} = \frac{a^2 + b^2}{b^2} $$

Por el teorema de Pitágoras:

$$ a^2 + b^2 = c^2 $$

Luego:

$$ \frac{A_1 + A_2}{A_2} = \frac{c^2}{b^2} $$

$$ \frac{A_1 + A_2}{A_2} = \frac{A_3}{A_2} $$

De donde se deduce:

$$ A_1 + A_2 = A_3 $$

Así queda demostrado que la suma de las áreas de los polígonos semejantes construidos sobre los catetos de un triángulo rectángulo es igual al área del polígono semejante sobre la hipotenusa.