Criterio de equivalencia de triángulos
Dos triángulos son equivalentes cuando tienen bases congruentes y alturas correspondientes.
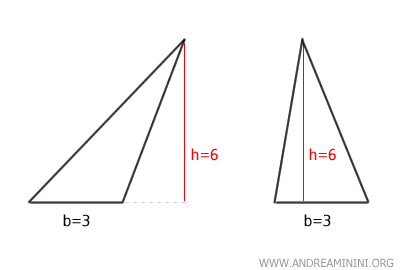
En otras palabras, si dos triángulos comparten la misma base y la misma altura, poseen la misma área (superficie equivalente).
Por lo tanto, son polígonos equivalentes.
Un ejemplo práctico
Consideremos, por ejemplo, dos triángulos no congruentes.
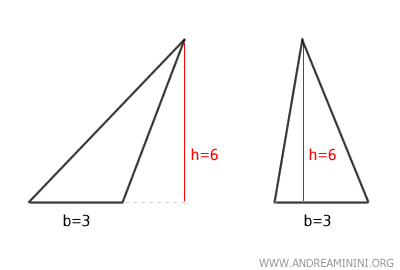
Ambos triángulos tienen la misma base, b = 3, y la misma altura, h = 6.
El área de un triángulo se calcula como la mitad del producto de la base por la altura:
$$ Área = \frac{b \cdot h}{2} $$
En este caso, como b = 3 y h = 6, obtenemos:
$$ Área = \frac{3 \cdot 6}{2} = \frac{18}{2} = 9 $$
Por tanto, con un área de 9, los dos triángulos son polígonos equivalentes.
Demostración
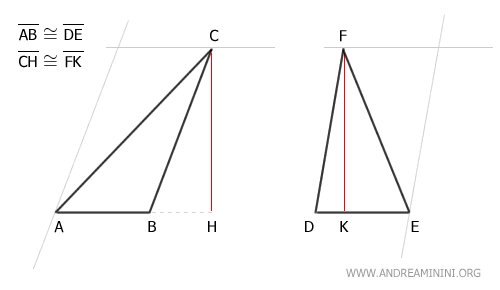
Consideremos dos triángulos no congruentes, ABC y DEF.
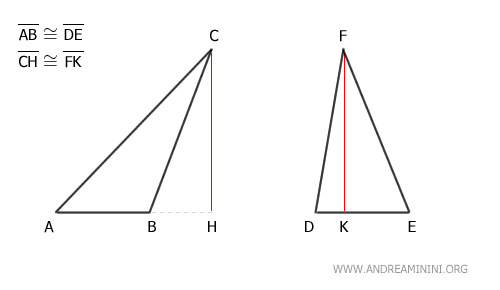
Según la hipótesis, ambos triángulos tienen la misma base y la misma altura:
$$ \overline{AB} \cong \overline{DE} $$
$$ \overline{CH} \cong \overline{DK} $$
Queremos demostrar que son polígonos equivalentes, es decir, que tienen la misma área.
Dado que el área de un triángulo es el producto de su base por su altura dividido entre dos:
$$ Área = \frac{base \cdot altura}{2} $$
y como los triángulos ABC y DEF tienen la misma base AB ≅ DE y la misma altura CH ≅ DK, resulta que:
$$ Área (ABC) = Área (DEF) = \frac{\overline{AB} \cdot \overline{CH}}{2} = \frac{\overline{DE} \cdot \overline{DK}}{2} $$
Por lo tanto, los dos triángulos son equivalentes.
Esto basta para demostrar el teorema.
Demostración alternativa
Existe otra manera de demostrar que los triángulos ABC y DEF son equivalentes.
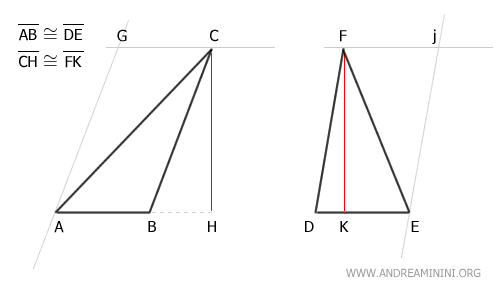
Se trazan líneas paralelas a las bases AB y DE que pasan por los vértices opuestos C y F:
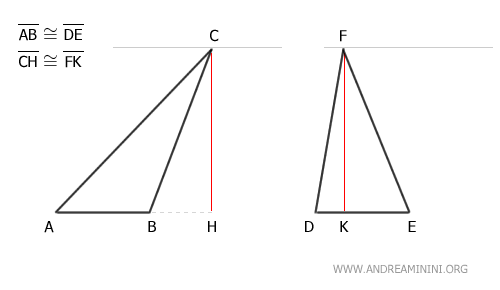
A continuación, se trazan líneas paralelas a los lados BC y DF que pasan también por los vértices C y F:
De este modo se obtienen dos paralelogramos: ABCG y DEFJ.
Estos paralelogramos tienen exactamente el doble de área que los triángulos ABC y DEF, respectivamente:
$$ Área (ABCG) = 2 \cdot Área (ABC) $$
$$ Área (DEFJ) = 2 \cdot Área (DEF) $$
Según el teorema de equivalencia de paralelogramos, los paralelogramos ABCG y DEFJ son equivalentes, ya que poseen bases congruentes AB ≅ DE y alturas congruentes CH ≅ DK.
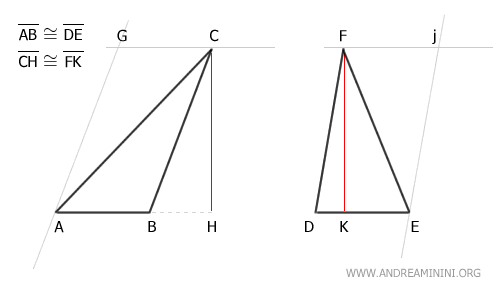
Por lo tanto, tienen áreas equivalentes:
$$ ABCG \doteq DEFJ $$
es decir:
$$ Área (ABCG) = Área (DEFJ) $$
Como hemos visto, el área de ABCG es el doble del área de su triángulo correspondiente, y lo mismo ocurre con DEFJ:
$$ Área (ABCG) = 2 \cdot Área (ABC) = 2 \cdot Área (DEF) = Área (DEFJ) $$
Si dividimos todo entre dos:
$$ \frac{Área (ABCG)}{2} = \frac{2 \cdot Área (ABC)}{2} = \frac{2 \cdot Área (DEF)}{2} = \frac{Área (DEFJ)}{2} $$
$$ \frac{Área (ABCG)}{2} = Área (ABC) = Área (DEF) = \frac{Área (DEFJ)}{2} $$
De aquí se concluye que las áreas de los triángulos ABC y DEF son iguales:
$$ Área (ABC) = Área (DEF) $$
Por lo tanto, los triángulos ABC y DEF tienen áreas equivalentes.
En consecuencia, los dos triángulos son equivalentes:
$$ Área (ABC) \doteq Área (DEF) $$
Con lo cual queda demostrada la proposición.