Reducción de lados en polígonos convexos
Todo polígono convexo es siempre equivalente a otro polígono con menos lados y la misma área.
Este principio se basa en que es posible reducir el número de lados de un polígono mediante descomposición y reordenamiento.
Obviamente, el triángulo constituye una excepción, ya que no existe un polígono de solo dos lados. Por definición, un polígono debe tener al menos tres lados.
Este concepto resulta particularmente útil para demostrar que, en la geometría plana, cambiar la forma de un polígono no altera su área.
Nota: Este principio es aplicable tanto a polígonos convexos como cóncavos. Sin embargo, en los convexos, el proceso es mucho más sencillo e intuitivo. En los cóncavos, en cambio, puede requerir cortes y reordenamientos más complejos para resolver las concavidades.
Cómo construir un polígono equivalente con un lado menos
Existen distintas maneras de reducir el número de lados de un polígono.
Una posibilidad es descomponer el polígono en figuras más simples y volver a ensamblarlas con una configuración diferente.
Uno de los métodos más simples consiste en utilizar las diagonales del polígono.
Consideremos cualquier polígono, regular o irregular. En este ejemplo tomaremos un hexágono.
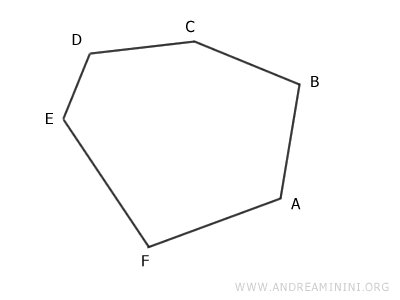
Se traza una diagonal entre dos vértices que tengan un vértice intermedio.
Por ejemplo, la diagonal entre A y C, con B como vértice intermedio.
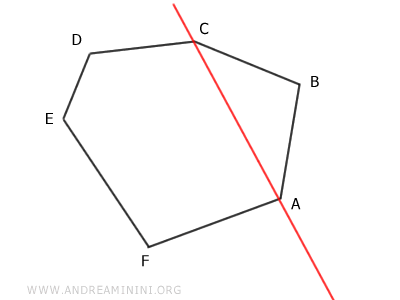
A continuación, se traslada dicha diagonal de modo que pase por el vértice intermedio B.
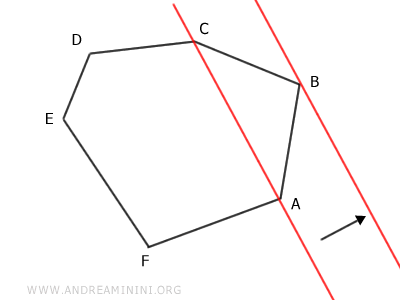
Después, se prolonga uno de los lados que parten de A o de C hasta que corte dicha línea.
Por ejemplo, se prolonga el lado AF hasta alcanzar el punto A'.
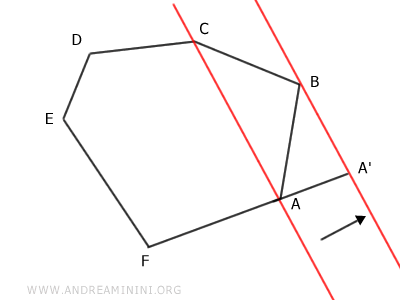
Luego se dibuja el segmento A'C que une el punto A' con el vértice C, eliminando así el vértice B del polígono.
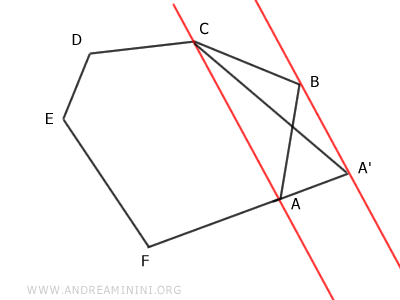
El resultado es un polígono A'CDEF de cinco lados, es decir, un pentágono.
Este nuevo pentágono es equivalente al hexágono inicial, lo que significa que conserva la misma área.
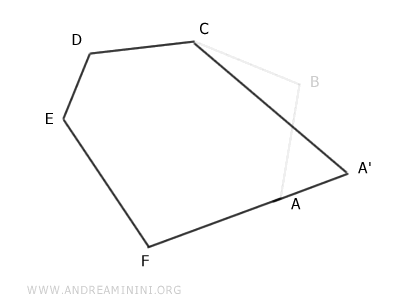
Demostración: Para comprobarlo, basta con observar los triángulos AA'C y ABC.
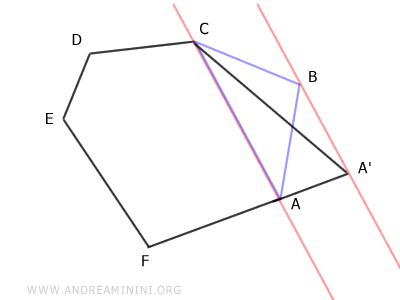
Estos dos triángulos tienen la misma base (AC) y la misma altura (AA'≅BB'). Por lo tanto, según el teorema de congruencia de triángulos, son triángulos equivalentes, es decir, de igual área.
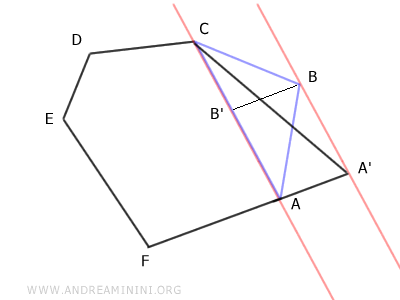
A partir de aquí, se puede observar que el hexágono está compuesto por el polígono ACDEF más el triángulo ABC: $$ ABCDEF \doteq ACDEF + ABC $$ El pentágono A'CDEF está compuesto por el polígono ACDEF más el triángulo AA'C: $$ A'CDEF \doteq ACDEF + AA'C $$ Dado que los triángulos ABC y AA'C son equivalentes, se deduce que tanto el hexágono como el pentágono son polígonos equidecomponibles, es decir, compuestos por las mismas figuras equivalentes: $$ ABCDEF \doteq ACDEF + ABC \doteq ACDEF + AA'C \doteq A'CDEF $$ $$ ABCDEF \doteq A'CDEF $$ Por lo tanto, el hexágono ABCDEF y el pentágono A'CDEF son equivalentes.
Repitiendo este mismo procedimiento, es posible reducir el pentágono A'CDEF a un cuadrilátero equivalente C'DEF (de cuatro lados).
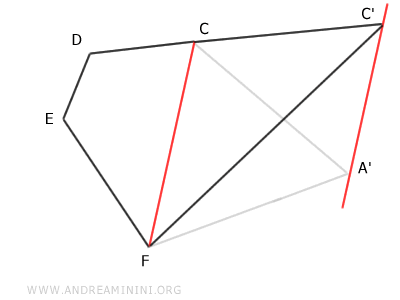
Finalmente, se puede reducir el cuadrilátero C'DEF a un triángulo equivalente C'D'F (de tres lados).
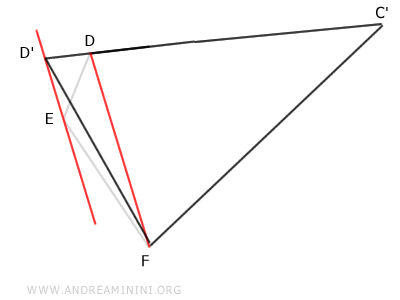
De este modo, se concluye que todo polígono convexo puede reducirse a un triángulo equivalente.
Nota: El método que he descrito para reducir el número de lados mediante el uso de diagonales no constituye un procedimiento formal en la geometría euclidiana. En la práctica, modificar el número de lados de un polígono manteniendo su área requiere técnicas de descomposición y reordenamiento que no son tan directas como simplemente trazar o desplazar diagonales.
Observaciones
Algunas consideraciones:
- Polígonos cóncavos
En el caso de los polígonos cóncavos, no siempre es posible reducir el número de lados sin alterar el área, al menos en el contexto de la geometría euclidiana.
Y así sucesivamente.