Cálculo del área de un polígono irregular

Determinar el área de un polígono irregular o de cualquier figura plana es una tarea más compleja que calcular el área de polígonos regulares. No obstante, existen diferentes métodos para lograrlo, en función de la información disponible y de las características concretas del polígono. A continuación te presento algunas de las técnicas más utilizadas:

Descomposición en polígonos regulares

Una figura plana puede descomponerse en elementos más simples, como triángulos, rectángulos, trapecios, entre otros.

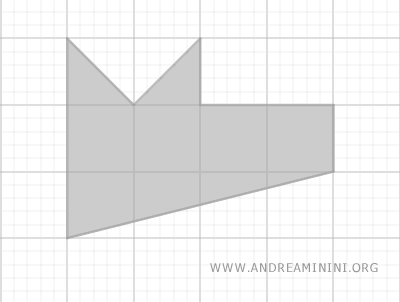
El área del polígono irregular se calcula sumando las áreas de estas figuras elementales.

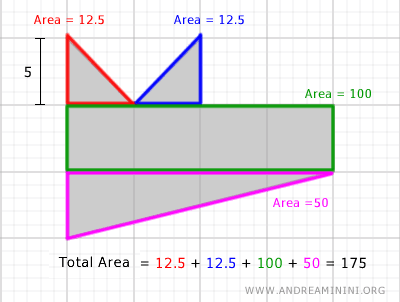
Cuando una figura, o parte de ella, no puede dividirse en polígonos regulares, se recurre a una estimación.

Por ejemplo, considera esta figura curvilínea:

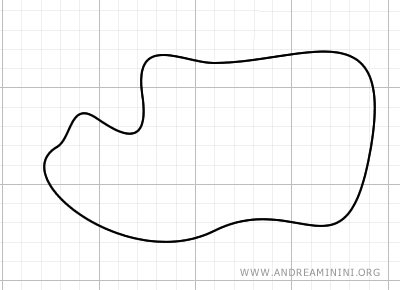
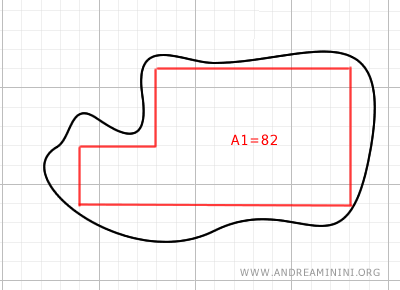
Para estimar su área, se traza un polígono interior que ajuste lo mejor posible a la figura, procurando minimizar los espacios vacíos.

Después, se descompone dicho polígono en polígonos regulares, se calcula el área de cada uno y se suman todas las áreas parciales.

Así obtenemos el área A1=82 correspondiente al polígono inscrito.

A continuación, se dibuja un polígono exterior que envuelva completamente la figura curvilínea, nuevamente buscando reducir al máximo los espacios sobrantes.

Luego, este polígono circunscrito se divide en polígonos regulares, se calcula el área de cada uno y se suman.

De este modo se obtiene el área A2 del polígono circunscrito.

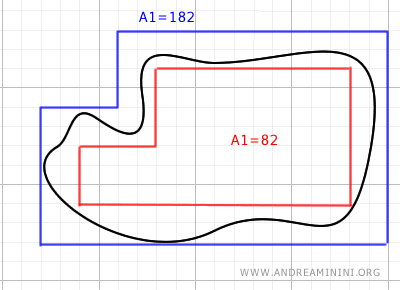
En este punto, podemos afirmar que el área de la figura irregular se encuentra comprendida entre el área del polígono inscrito A1=82 y la del polígono circunscrito A2=182.

$$ A_1 < A < A_2 $$

$$ 82 < A < 182 $$

Finalmente, se obtiene un valor aproximado calculando el promedio de ambos resultados:

$$ A = \frac{A_1 + A_2}{2} $$

$$ A = \frac{82 + 182}{2} $$

$$ A = \frac{264}{2} $$

$$ A = 132 $$

Así, el área aproximada de la figura plana es de 132 unidades cuadradas.

Este método permite obtener una estimación razonablemente precisa del área de cualquier figura plana.

Nota: Por supuesto, se trata de una aproximación. Su precisión dependerá del nivel de detalle en la descomposición. Cuanto más pequeños sean los polígonos utilizados en la estimación, mayor será la exactitud del resultado.

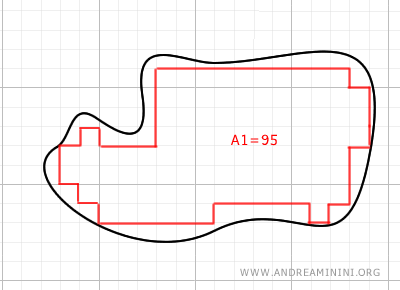
Este método aproximado está desarrollado en el análisis matemático y constituye la base de la integral definida de Riemann.

La fórmula del zapatero (o fórmula del área de Gauss)

Esta fórmula resulta especialmente útil si se conocen las coordenadas de los vértices del polígono irregular. Si el polígono tiene vértices en (x₁,y₁), (x₂,y₂), ..., (x_n,y_n), y se cierra con el vértice (x_n+1,y_n+1) = (x₁,y₁), el área A del polígono se calcula mediante la siguiente expresión:

$$ A = \frac{1}{2} \cdot \left| \sum_{i=1}^{n} ( x_i y_{i+1} - x_{i+1} y_i ) \right| $$

Veamos un ejemplo con este polígono irregular:

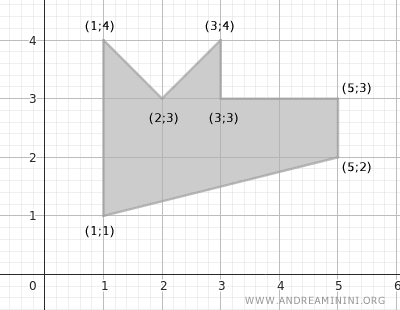
Las coordenadas de sus vértices son:

$$ (x_1;y_1) = (1;1) \\ (x_2;y_2) = (1;4) \\ (x_3;y_3) = (2;3) \\ (x_4;y_4) = (3;4) \\ (x_5;y_5) = (3;3) \\ (x_6;y_6) = (5;3) \\ (x_7;y_7) = (5;2) $$

Para cerrar el polígono, añadimos un vértice adicional coincidente con el inicial:

$$ (x_8;y_8) = (1;1) $$

Ahora aplicamos la fórmula para obtener la suma:

$$ A = \frac{1}{2} \cdot \left| \sum_{i=1}^{7} ( x_i y_{i+1} - x_{i+1} y_i ) \right| $$

$$ A = \frac{1}{2} \cdot \left| (x_1 y_2 - x_2 y_1) + (x_2 y_3 - x_3 y_2) + (x_3 y_4 - x_4 y_3) + \\ \ \ \ \ + (x_4 y_5 - x_5 y_4) + (x_5 y_6 - x_6 y_5) + (x_6 y_7 - x_7 y_6) + (x_7 y_8 - x_8 y_7) \right| $$

Sustituyendo los valores de las coordenadas: x₁=1, x₂=1, x₃=2, x₄=3, x₅=3, x₆=5, x₇=5, x₈=1; y₁=1, y₂=4, y₃=3, y₄=4, y₅=3, y₆=3, y₇=2, y₈=1

$$ A = \frac{1}{2} \cdot \left| (1 \cdot 4 - 1 \cdot 1) + (1 \cdot 3 - 2 \cdot 4) + (2 \cdot 4 - 3 \cdot 3) + \\ \ \ \ \ + (3 \cdot 3 - 3 \cdot 4) + (3 \cdot 3 - 5 \cdot 3) + (5 \cdot 2 - 5 \cdot 3) + (5 \cdot 1 - 1 \cdot 2) \right| $$

Realizando los cálculos:

$$ A = \frac{1}{2} \cdot \left| (4 - 1) + (3 - 8) + (8 - 9) + (9 - 12) + (9 - 15) + (10 - 15) + (5 - 2) \right| $$

$$ A = \frac{1}{2} \cdot \left| 3 - 5 - 1 - 3 - 6 - 5 + 3 \right| $$

$$ A = \frac{1}{2} \cdot |-14| $$

$$ A = \frac{1}{2} \cdot 14 $$

$$ A = 7 $$

Como cada celda de la cuadrícula equivale a 5x5=25 unidades cuadradas,

El área del polígono irregular es 25×7, es decir, 175 unidades cuadradas.

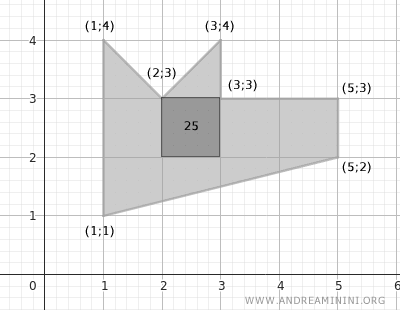
Este es el mismo resultado que se había obtenido previamente.

Y así sucesivamente.