Apotema
El apotema de un polígono regular es el segmento que une el centro del polígono con el punto medio de uno de sus lados, formando un ángulo recto con dicho lado.
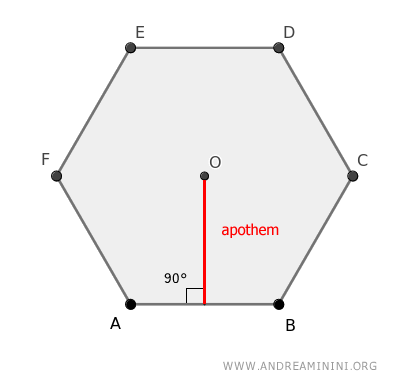
En otras palabras, el apotema es la distancia desde el centro del polígono hasta cualquiera de sus lados.
En los polígonos regulares, el apotema coincide con el radio de la circunferencia inscrita en el polígono, es decir, con el inradio.
Relación entre el apotema y el lado en un polígono regular
La razón entre el apotema (a) y la longitud del lado (l) es constante para cada tipo de polígono, y se conoce como su "número fijo" o constante f: $$ f = \frac{a}{l} $$ Esta constante depende exclusivamente del número de lados del polígono.
El número fijo permanece inalterado, sea cual sea el tamaño del polígono o la longitud de sus lados.
Cada tipo de polígono regular tiene su propio número fijo característico.
Por ejemplo, en un pentágono, la constante f es un decimal no periódico: 0.688... que suele aproximarse como 0.688. En un hexágono, es aproximadamente 0.866.
He aquí una tabla con los valores de f para algunos polígonos comunes:
| Polígono | Constante f |
|---|---|
| Triángulo equilátero | 0.289... |
| Cuadrado | 0.5 |
| Pentágono | 0.688... |
| Hexágono | 0.866... |
| Heptágono | 1.038... |
| Octágono | 1.207... |
| Eneágono | 1.374... |
| Decágono | 1.539... |
| Dodecágono | 1.866... |
¿Por qué es importante conocer la constante f?
Conociendo la constante f es posible calcular la longitud del lado a partir del apotema: $$ l = \frac{a}{f} $$ o bien obtener el apotema a partir del lado: $$ a = l \cdot f $$
Por ejemplo, en un hexágono de lado 6 cm:
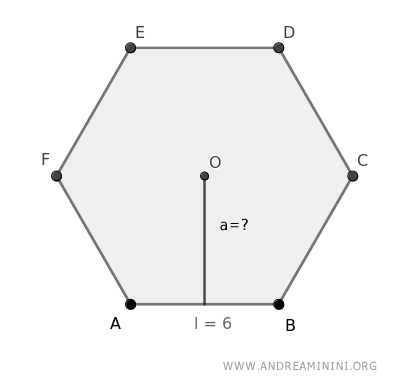
el apotema se calcula así: $$ a = l \cdot f $$ $$ a = 6 \cdot 0.866 $$ $$ a = 5.196 $$
La constante f también resulta muy útil para calcular el área de un polígono regular:
$$ A = n \cdot \frac{l \cdot a}{2} $$
Como $$ a = l \cdot f $$, podemos sustituir:
$$ A = n \cdot \frac{l \cdot (l \cdot f)}{2} $$
$$ A = n \cdot \frac{l^2 \cdot f}{2} $$
El producto de la mitad del número de lados por la constante f se conoce como constante φ (se pronuncia “fi”):
$$ \phi = \frac{n \cdot f}{2} $$
Esta constante, que depende de f, también varía en función del número de lados.
De este modo, la fórmula del área queda:
$$ A = l^2 \cdot \phi $$
Aquí algunos valores aproximados de φ:
| Polígono | Constante φ |
|---|---|
| Triángulo equilátero | 0.433... |
| Cuadrado | 1 |
| Pentágono | 1.72... |
| Hexágono | 2.598... |
| Heptágono | 3.634... |
| Octágono | 4.828... |
| Eneágono | 6.182... |
| Decágono | 7.694... |
| Dodecágono | 11.196... |
Nota: Las fórmulas inversas también resultan muy útiles cuando se trabaja con la constante φ. Por ejemplo, si conoces el área (A) de un polígono regular, puedes hallar la longitud del lado: $$ l = \sqrt{ \frac{A}{\phi} } $$ Esta fórmula se obtiene despejando l a partir de: $$ A = l^2 \cdot \phi $$ $$ l^2 = \frac{A}{\phi} $$ $$ l = \sqrt{ \frac{A}{\phi} } $$
Y así sucesivamente.