Teorema de la Suma de los Ángulos Interiores en un Polígono Convexo
En un polígono convexo de n lados, la suma de sus ángulos interiores es igual a (n-2) ángulos llanos (de 180° cada uno). $$ (n-2) \cdot 180° $$
La suma de los ángulos interiores de un polígono convexo depende exclusivamente del número de lados que posea.
Por ejemplo, un triángulo tiene n = 3 lados.
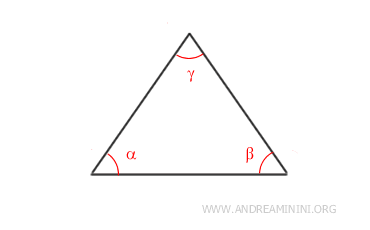
Así, la suma de los ángulos interiores de un triángulo es 180°.
$$ (n-2) \cdot 180° $$
$$ (3-2) \cdot 180° = 180° $$
Por su parte, un rectángulo cuenta con n = 4 lados.
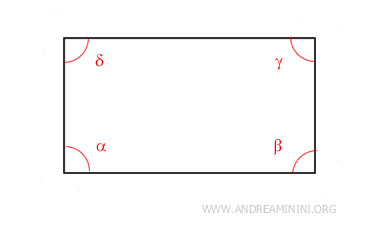
En este caso, la suma de los ángulos interiores del rectángulo es 360°.
$$ (n-2) \cdot 180° $$
$$ (4-2) \cdot 180° $$
$$ 2 \cdot 180° = 360° $$
Del mismo modo, un pentágono, con n = 5 lados, obedece la misma regla.
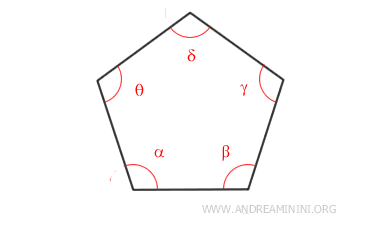
Por tanto, la suma de sus ángulos interiores es 540°.
$$ (n-2) \cdot 180° $$
$$ (5-2) \cdot 180° $$
$$ 3 \cdot 180° = 540° $$
Este patrón se cumple para cualquier polígono convexo, sin importar el número de lados.
Demostración del Teorema
La demostración es sumamente sencilla.
Consideremos un polígono convexo cualquiera con n lados; por ejemplo, uno con n = 5.
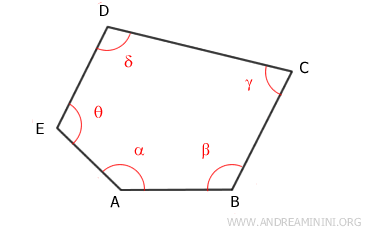
El polígono puede ser regular o irregular; esto no influye en absoluto. Lo esencial es que sea convexo.
Seleccionamos un punto interior $ P $ y trazamos segmentos que lo unan con todos los vértices del polígono.
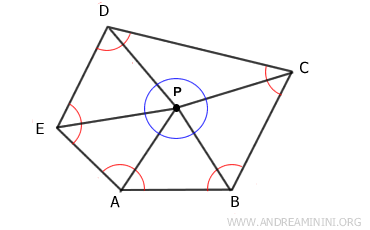
De este modo, el polígono queda dividido en $ n $ triángulos.
Sabemos que la suma de los ángulos interiores de cada triángulo es 180°. Por lo tanto, la suma total de los ángulos interiores del polígono equivale a la suma de los ángulos de esos $ n $ triángulos, menos la suma de los ángulos alrededor del punto $ P $, que en conjunto suman 360°.
$$ n \cdot 180° - 360° $$
Una sencilla reducción algebraica conduce a:
$$ n \cdot 180° - 2 \cdot 180° $$
$$ (n - 2) \cdot 180° $$
Y de este modo queda verificada la fórmula inicial.
Nota. En el caso de $ n = 5 $, la suma de los ángulos interiores de un polígono convexo de 5 lados es 540°: $$ (5 - 2) \cdot 180° = 3 \cdot 180° = 540° $$
Demostración Alternativa
Otra manera de probar este teorema consiste en partir nuevamente de un polígono convexo de n lados, por ejemplo, n = 5.

Elegimos un vértice cualquiera y trazamos desde él todas las diagonales posibles.
Por ejemplo, seleccionemos el vértice A.
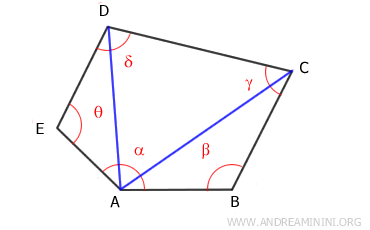
Desde un solo vértice de un polígono pueden trazarse n-3 diagonales, dividiendo así el polígono en n-2 triángulos.
En este caso concreto, el polígono convexo se divide en tres triángulos: ADE, ACD y ABC.
$$ n - 2 = 5 - 2 = 3 \ \text{triángulos} $$
Este procedimiento simplifica notablemente el cálculo de la suma de los ángulos interiores, al descomponer el polígono en partes más sencillas y manejables.
Dado que sabemos que la suma de los ángulos interiores de un triángulo es 180°, y que el polígono ha quedado dividido en tres triángulos, podemos concluir que la suma de los ángulos interiores del polígono convexo es 180° multiplicado por tres.
$$ 180° \cdot 3 = 540° $$
Por tanto, la suma de los ángulos interiores de un polígono convexo de 5 lados es 540°.
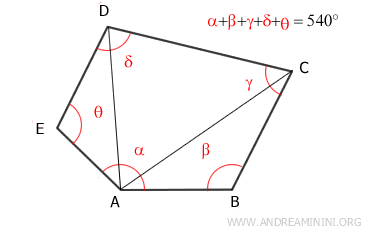
Y este método es perfectamente aplicable a polígonos con cualquier número de lados.