Hexágono

Un hexágono es una figura geométrica cerrada que cuenta con seis lados y seis ángulos.

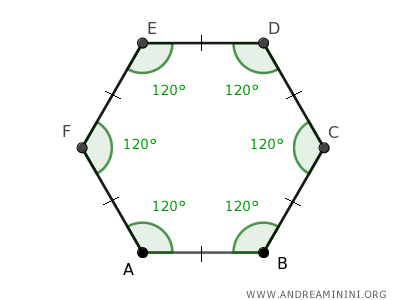
Cuando un hexágono presenta todos sus lados y ángulos iguales, se denomina específicamente hexágono regular.

Cada ángulo interno de un hexágono regular mide 120°.

Existen también los hexágonos irregulares, en los que los lados tienen longitudes distintas y sus ángulos no son congruentes.

En adelante, cuando me refiera a “hexágono”, estaré hablando del hexágono regular.

Fórmulas

A continuación, se presentan las fórmulas fundamentales para calcular el perímetro (P) y el área (A) de un hexágono:

• Perímetro
  El perímetro de un hexágono regular equivale a seis veces la longitud de uno de sus lados (l): $$ P = 6 \cdot l $$
• Área
  El área de un hexágono regular puede calcularse si se conoce la apotema (a): $$ A = \frac{P \cdot a}{2} \ \ \text{o} \ \ A = 2.598 \cdot l^2 $$ donde $ l $ es la longitud del lado y $ a $ la apotema del hexágono. $$ a = 0.866 \cdot l $$
• Longitud del lado
  La longitud del lado de un hexágono regular coincide con el radio de la circunferencia circunscrita (demostración): $$ l = r $$ Alternativamente, puede calcularse conociendo el radio (r) de la circunferencia inscrita (demostración): $$ l = \frac{2\sqrt{3}}{3} \cdot r $$ O bien, conociendo la apotema (a), que coincide con el radio de la circunferencia inscrita (r=a): $$ l = \frac{2\sqrt{3}}{3} \cdot a $$

Perímetro

El perímetro de un hexágono se obtiene simplemente multiplicando la longitud del lado por seis.

$$ P = 6 \cdot l $$

En ocasiones se emplea el símbolo “2p” para representar el perímetro, donde “p” (en minúscula) es el semiperímetro.

$$ 2p = 6 \cdot l $$

Esto se debe a que la letra minúscula “p” se utiliza para designar el semiperímetro de un polígono.

$$ p = \frac{P}{2} $$

Mientras que la letra mayúscula “P” indica el perímetro completo. Así, P=2p.

Ejemplo: Consideremos un hexágono regular con una longitud de lado l=2.

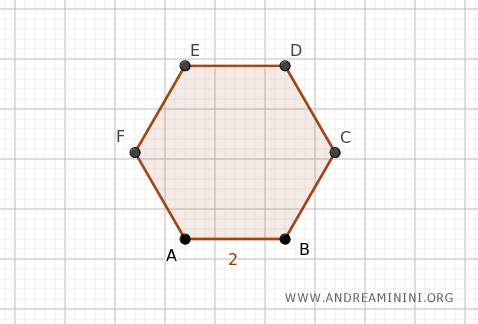
Como un hexágono tiene n=6 lados, su perímetro es P=12 $$ P = n \cdot l = 6 \cdot 2 = 12 $$ Por tanto, su semiperímetro es la mitad del perímetro, es decir, p=6 $$ p = \frac{P}{2} = \frac{12}{2} = 6 $$

Apotema

La apotema (a) de un hexágono corresponde al radio de la circunferencia inscrita.

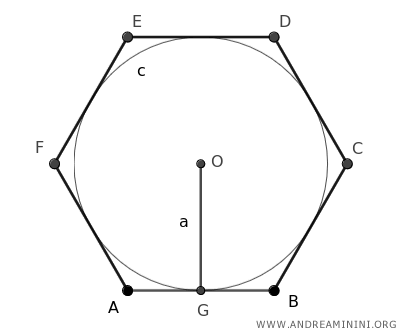
Se determina trazando un segmento (OG) desde el centro (O) hasta el punto medio de cualquiera de sus lados, de forma perpendicular.

Geométricamente, la apotema es la distancia perpendicular entre el centro del hexágono y uno de sus lados.

La fórmula para calcular la apotema en función de la longitud del lado “l” es:

$$ a = l \cdot f_1 $$

Donde f₁ es una constante propia de los hexágonos, cuyo valor es f₁ = 0.866.

¿Qué son los números fijos? En un hexágono regular, la relación entre la apotema “a” y la longitud del lado “l” es constante y vale 0.866 $$ f_1 = \frac{\sqrt{3}}{2} = 0.866 $$ Este valor se denomina “número fijo” porque se mantiene inalterable independientemente del tamaño del hexágono.

¿Para qué sirve?

La apotema es fundamental para distintos cálculos geométricos, especialmente para determinar el área del hexágono.

Área del Hexágono

El área de un hexágono regular puede obtenerse multiplicando el semiperímetro (p) por la apotema (a).

$$ A = p \cdot a $$

Aquí, “p” en minúscula representa el semiperímetro, mientras que P=2p en mayúscula corresponde al perímetro completo. Por tanto, el semiperímetro se calcula como p=P/2.

Ejemplo: Un hexágono regular tiene una longitud de lado l=2.

Así, con n=6 lados, su perímetro es P=12 $$ P = n \cdot l = 6 \cdot 2 = 12 $$ Por tanto, su semiperímetro es p=6 $$ p = \frac{P}{2} = \frac{12}{2} = 6 $$ Calculamos ahora la apotema del hexágono: $$ a = 0.866 \cdot l = 0.866 \cdot 2 = 1.732 $$ Finalmente, hallamos el área del hexágono utilizando p=6 y a=1.732: $$ A = p \cdot a = 6 \cdot 1.732 = 10.392 $$ Por tanto, el área del hexágono es 10.392.

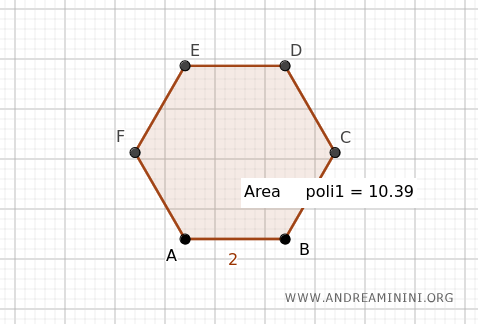
Método Alternativo para Calcular el Área

Otra forma de calcular el área del hexágono consiste en emplear los números fijos característicos de este polígono.

$$ A = l^2 \cdot f_2 $$

Aquí, “l” representa la longitud del lado y f₂ es una constante específica de los hexágonos, cuyo valor es f₂ = 2.598.

Ejemplo: Tomemos el mismo hexágono regular del ejemplo anterior, con longitud de lado l=2.

Para calcular el área, multiplicamos el cuadrado de la longitud del lado por el número fijo f₂ = 2.598: $$ A = l^2 \cdot f_2 = 2^2 \cdot 2.598 = 4 \cdot 2.598 = 10.392 $$ El área del hexágono es 10.392, coincidiendo con el resultado obtenido mediante el método anterior.

Números Fijos del Hexágono

Los números fijos de un hexágono son f₁ = 0.866 y f₂ = 2.598. $$ f_1 = \frac{a}{l} = 0.866 $$ $$ f_2 = 2.598 $$ Resultan especialmente útiles para calcular la apotema y el área de un hexágono.

Existe una relación directa entre ambos números fijos, f₁ y f₂.

Sabemos que el área de un hexágono puede obtenerse multiplicando el semiperímetro (p) por la apotema (a):

$$ A = p \cdot a $$

En un hexágono regular, la razón entre la apotema (a) y la longitud del lado (l) es un valor constante de 0.866.

$$ f_1 = \frac{a}{l} = 0.866 $$

Nota: A veces, el número fijo f₁ se expresa también como la raíz cuadrada de 3 dividida entre 2: $$ f_1 = \frac{\sqrt{3}}{2} = 0.866 $$ Esta relación se debe a que un hexágono regular puede descomponerse en seis triángulos equiláteros.

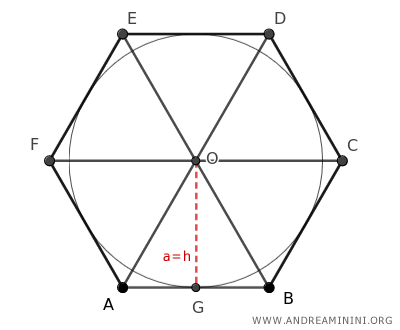
La altura (h) de cada triángulo equilátero que compone el hexágono coincide exactamente con la apotema (a): $$ a = h $$ Sabiendo que la altura (h) de un triángulo equilátero se calcula como el producto de la longitud del lado (l) por √3/2: $$ h = \frac{\sqrt{3}}{2} \cdot l $$ Si consideramos un lado unitario, l=1, obtenemos el número fijo f₁ = 0.866: $$ a = h = \frac{\sqrt{3}}{2} = 0.866 $$

Por tanto, la apotema de un hexágono se calcula mediante la fórmula a = l · 0.866

$$ A = p \cdot a $$

$$ A = p \cdot (l \cdot 0.866) $$

El semiperímetro p = P/2 es la mitad del perímetro del hexágono.

$$ A = \frac{P}{2} \cdot (l \cdot 0.866) $$

A su vez, el perímetro P = n · l se obtiene multiplicando el número de lados (n = 6) por la longitud del lado “l”.

$$ A = \frac{n \cdot l}{2} \cdot l \cdot 0.866 $$

$$ A = \frac{6 \cdot l}{2} \cdot l \cdot 0.866 $$

$$ A = \frac{6 \cdot 0.866}{2} \cdot l^2 $$

$$ A = 2.598 \cdot l^2 $$

Aquí, 2.598 corresponde al número fijo f₂ del hexágono.

Notas Adicionales

A continuación, algunas observaciones y datos adicionales sobre los hexágonos:

• Construcción de un Hexágono Regular
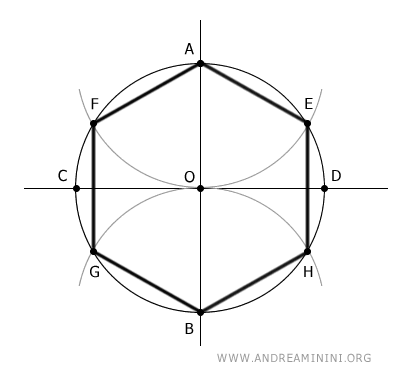
  Un hexágono regular puede construirse únicamente utilizando regla y compás.
  
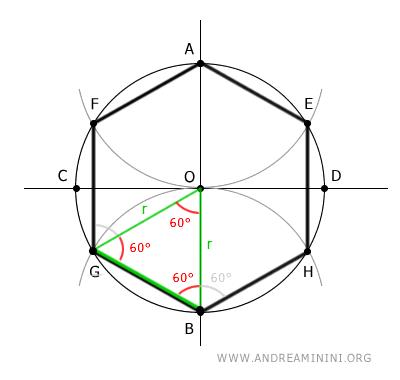
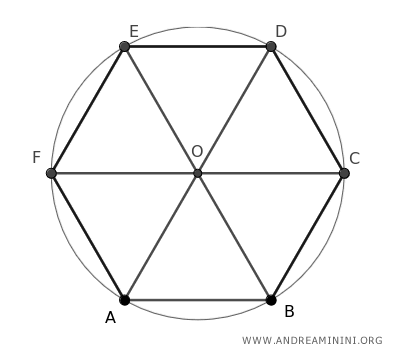
• El Lado de un Hexágono Regular es Igual al Radio de la Circunferencia Circunscrita
  La longitud del lado de un hexágono regular coincide exactamente con el radio de su circunferencia circunscrita. Esto se explica porque cada triángulo formado por un lado del hexágono y dos radios de la circunferencia es equilátero.
  
• Relación entre el Lado del Hexágono y el Radio de la Circunferencia Inscrita y la Apotema
  La longitud del lado de un hexágono regular está relacionada con el radio de su circunferencia inscrita (r) y con la apotema (a), que en este caso coinciden (r = a), mediante la fórmula: $$ l = \frac{2\sqrt{3}}{3} \cdot r $$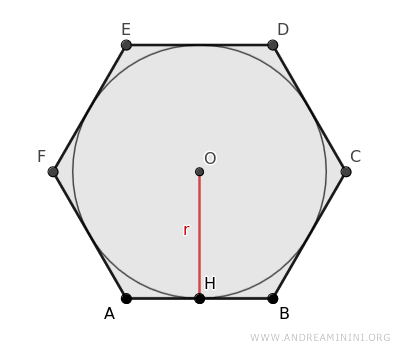
• Optimización del Espacio
  Entre los polígonos, el hexágono regular destaca por su armonía y simetría. Todos sus lados son iguales y sus ángulos internos poseen idéntica medida. Esta regularidad le confiere equilibrio visual y gran estabilidad estructural. La capacidad de los hexágonos regulares para encajar perfectamente entre sí, sin dejar espacios, es la base de las teselaciones.
  
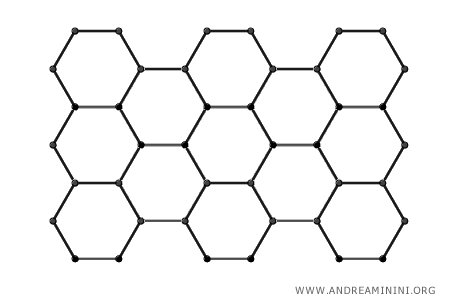
  Por esta razón, los hexágonos se utilizan con frecuencia para optimizar el espacio. En arquitectura e ingeniería, por ejemplo, se emplean celdas hexagonales en el diseño de estructuras. En biología, las abejas construyen panales con forma hexagonal y, en geografía económica, los hexágonos se emplean para analizar patrones de localización.
• El Lado de un Hexágono es Congruente con el Radio de la Circunferencia Circunscrita
  La longitud del lado de un hexágono es igual al radio de su circunferencia circunscrita. Esta propiedad se explica porque el hexágono puede dividirse en seis triángulos equiláteros.
  
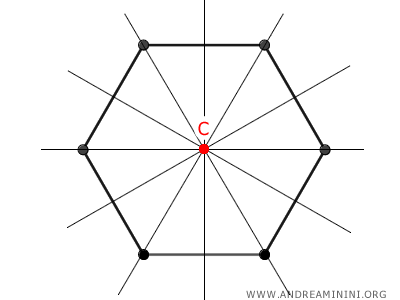
• Un hexágono posee un centro de simetría y seis ejes de simetría que pasan por su centro.
  

Y así sucesivamente.