Polígonos
Un polígono es una figura plana delimitada por una línea poligonal cerrada, que no se cruza a sí misma, y por todos los puntos que se encuentran en su interior.
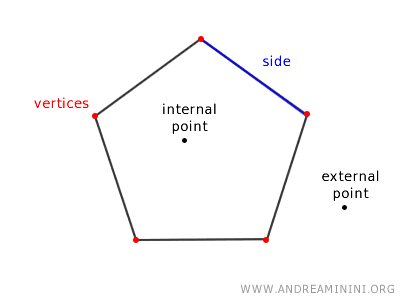
Los segmentos que forman esta línea poligonal cerrada se denominan lados del polígono.
Los extremos de dichos lados reciben el nombre de vértices del polígono.
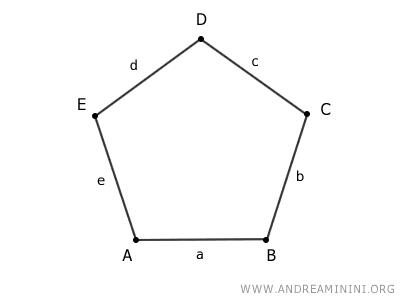
Habitualmente, los lados de un polígono se designan con letras minúsculas, mientras que los vértices se representan con letras mayúsculas.
La palabra "polígono" procede del griego antiguo: πολύς (polys, "muchos") y γωνία (gōnia, "ángulo"), y significa "muchos ángulos". En geometría plana, un polígono siempre posee al menos tres lados, ya que para formar una línea poligonal cerrada se requieren, como mínimo, tres puntos distintos (vértices).
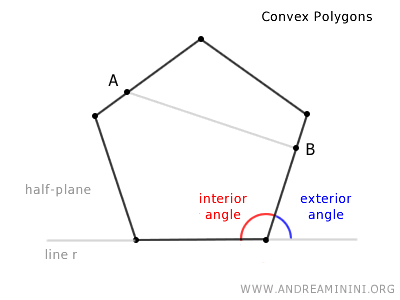
Cada vértice de un polígono tiene un ángulo interior y un ángulo exterior.
Los puntos que se encuentran sobre la línea poligonal cerrada conforman el perímetro del polígono.
Los puntos que quedan dentro de esa línea se llaman puntos interiores, mientras que los que están fuera reciben el nombre de puntos exteriores.
Clasificación de los polígonos
Existen diversas formas de clasificar los polígonos.
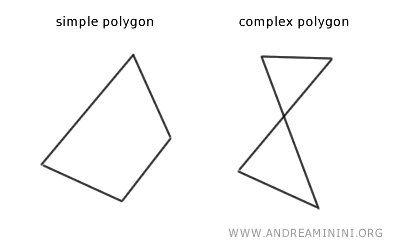
Por ejemplo, un polígono se denomina "polígono simple" si ninguno de sus lados no consecutivos se cruza entre sí.
Si en cambio se cruzan, se habla de un "polígono complejo" (también conocido como "polígono auto-intersecante").
Otra forma de clasificarlos se basa en la congruencia de sus lados y ángulos.
Un polígono se llama polígono regular si todos sus lados y todos sus ángulos son congruentes, es decir, tienen la misma medida.
Si no es así, se clasifica como polígono irregular.
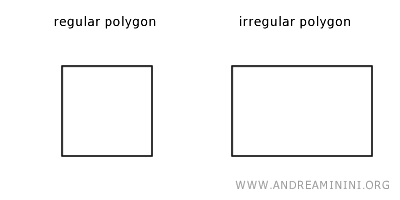
Por ejemplo, un cuadrado es un polígono regular porque todos sus lados y ángulos son iguales. En cambio, un rectángulo es un polígono irregular, ya que sus lados no tienen la misma longitud. De forma análoga, un triángulo equilátero es regular, mientras que un triángulo escaleno es irregular.
También se pueden clasificar los polígonos en función de su concavidad o convexidad, o bien por el número de ángulos que presentan.
Polígonos convexos y cóncavos
Un polígono puede ser convexo o cóncavo.
- Polígonos convexos
Un polígono convexo es aquel en el que, al tomar dos puntos cualesquiera A y B en su interior, el segmento AB que los une permanece íntegramente dentro del polígono. Es decir, ningún punto del segmento se encuentra fuera de la figura. Los polígonos convexos tienen todos sus ángulos interiores menores de 180 grados.

Nota: Un polígono convexo tiene exclusivamente ángulos convexos. Además, si se traza una recta que contenga uno de sus lados, el polígono queda por completo situado en uno de los dos semiplanos definidos por dicha recta.
- Polígonos cóncavos
Un polígono cóncavo (o no convexo) es aquel en el que existen al menos dos puntos A y B tales que el segmento AB que los une no está totalmente contenido dentro del polígono. En otras palabras, parte de ese segmento se encuentra fuera de la figura.
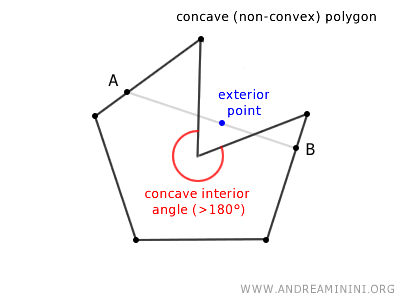
Nota: Un polígono cóncavo debe tener al menos cuatro lados. Además, necesariamente cuenta con al menos un ángulo interior mayor de 180 grados, lo que significa que posee al menos un ángulo interior cóncavo.
Tipos de polígonos
Los polígonos reciben nombres distintos según la cantidad de ángulos que poseen.
| Polígono | Ángulos |
|---|---|
| Triángulo | 3 ángulos |
| Cuadrilátero | 4 ángulos |
| Pentágono | 5 ángulos |
| Hexágono | 6 ángulos |
| Heptágono | 7 ángulos |
| Octágono | 8 ángulos |
| Eneágono | 9 ángulos |
| Decágono | 10 ángulos |
| Hendecágono | 11 ángulos |
| Dodecágono | 12 ángulos |
Diagonales y cuerdas de un polígono
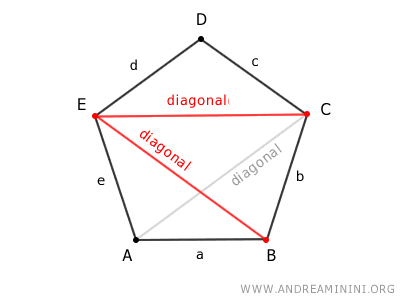
Una diagonal de un polígono es un segmento que une dos vértices que no son consecutivos.
Por ejemplo, los segmentos EC y EB son dos diagonales del polígono.
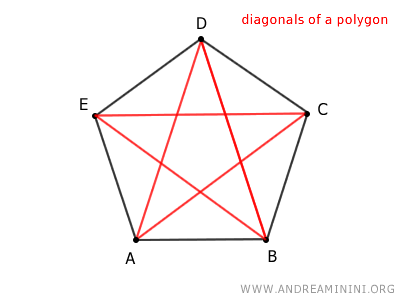
¿Cuántas diagonales tiene un polígono? Un polígono con n vértices tiene n·(n-3)/2 diagonales. $$ \frac{n \cdot (n-3)}{2} $$ Por ejemplo, un pentágono tiene n=5 lados, por lo que posee 5 diagonales: $$ \frac{5 \cdot (5-3)}{2} = \frac{5 \cdot 2}{2} = \frac{10}{2} = 5 $$ Para comprobarlo, basta dibujar todas las diagonales del pentágono y contarlas.
Una cuerda de un polígono es un segmento que une dos puntos cualesquiera del perímetro que no se encuentren sobre el mismo lado.
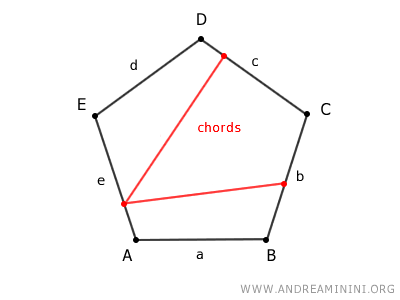
Todo polígono tiene infinitas cuerdas, ya que los puntos que conforman su perímetro son infinitos.
Observaciones
A continuación, se presentan algunas observaciones, propiedades y notas relevantes sobre los polígonos.
- Dos polígonos son congruentes si pueden superponerse mediante un movimiento rígido
Los polígonos congruentes tienen lados y ángulos iguales dispuestos en el mismo orden, lo que significa que poseen las mismas dimensiones. - Perímetro de un polígono
El perímetro de un polígono es igual a la suma de las longitudes de todos sus lados. - La suma de los ángulos interiores de un polígono con n lados se calcula con la fórmula $$ (n-2) \cdot 180° $$
Por ejemplo, un cuadrado tiene n=4 lados. Por tanto, la suma de sus ángulos interiores es 360°. $$ (4-2) \cdot 180° = 2 \cdot 180° = 360° $$ En efecto, un cuadrado posee cuatro ángulos rectos de 90° cada uno.
- Un polígono con n lados tiene n vértices y n ángulos.
Cada lado de un polígono se encuentra delimitado por dos vértices. No obstante, dado que cada vértice pertenece a dos lados, el número total de vértices coincide con el número de lados. De forma similar, cada vértice está asociado a un ángulo, por lo que la cantidad de ángulos es también igual al número de lados.