Ángulos Exteriores

Los ángulos exteriores se forman en la intersección entre uno de los lados de un polígono y la prolongación de su lado contiguo.

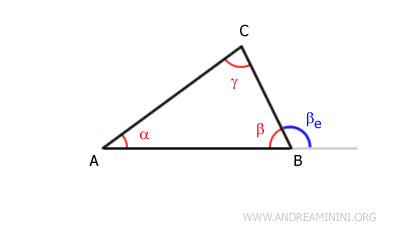
Por ejemplo, analicemos el triángulo ABC.

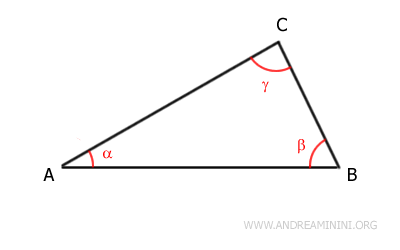
Este triángulo presenta tres ángulos interiores: α, β y γ.

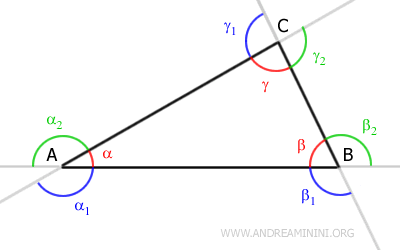
Recorriendo el triángulo en sentido antihorario, se distinguen los siguientes ángulos exteriores:

• El ángulo α₁ está delimitado entre la prolongación del lado AC y el lado AB.
• El ángulo α₂ está delimitado entre el lado AC y la prolongación del lado AB.
• El ángulo β₁ está delimitado entre el lado AB y la prolongación del lado BC.
• El ángulo β₂ está delimitado entre la prolongación del lado AB y el lado BC.
• El ángulo γ₁ está delimitado entre la prolongación del lado BC y el lado AC.
• El ángulo γ₂ está delimitado entre el lado BC y la prolongación del lado AC.

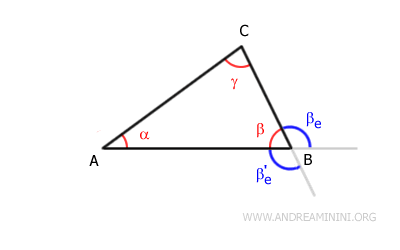
Cada ángulo interior posee dos ángulos exteriores adyacentes. Por ejemplo, el ángulo interior β está asociado a dos ángulos exteriores adyacentes: β_e y β_e'.

Observaciones

Veamos algunas observaciones relevantes sobre la suma de los ángulos:

• Suma de los ángulos exteriores
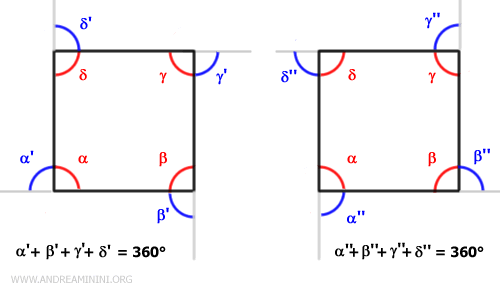
  La suma de los ángulos exteriores de cualquier polígono es siempre 360°, independientemente del número de lados.

  Ejemplo: Un cuadrado tiene 4 lados y 4 ángulos interiores de 90°. Aunque en cada vértice pueden definirse dos ángulos exteriores adyacentes, solo se consideran 4 ángulos exteriores, uno por vértice. La suma de estos ángulos exteriores es, en todos los casos, 360°.
  

• Teorema del Ángulo Exterior
  En un triángulo, cada ángulo exterior es mayor que cualquiera de los ángulos interiores que no son adyacentes a él.

  Ejemplo: En el triángulo ABC, el ángulo exterior β_e es mayor que cada uno de los ángulos interiores que no son contiguos a él: α y γ.
  
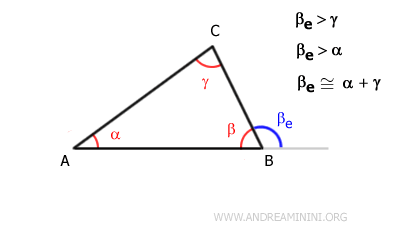
  El ángulo interior β no se tiene en cuenta, ya que es adyacente al ángulo exterior β_e.

• Relación entre ángulos interiores y exteriores
  En cualquier polígono, la suma de un ángulo interior y su ángulo exterior adyacente equivale siempre a un ángulo llano de 180°.

  Ejemplo: En el triángulo ABC, la suma del ángulo interior β y el ángulo exterior β_e conforma un ángulo llano (180°).
  

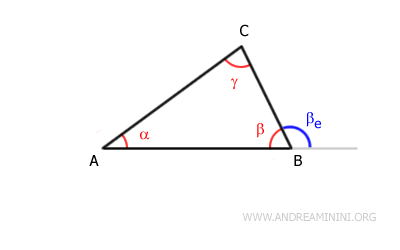
Y así sucesivamente.