Bisectriz de un Ángulo

La bisectriz de un ángulo es una semirrecta que parte del vértice y divide el ángulo en dos partes iguales, generando dos ángulos congruentes.

Por ejemplo, consideremos un ángulo de 60°.

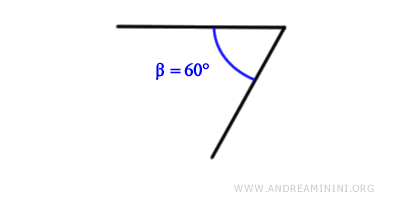
La bisectriz de este ángulo es una semirrecta que nace en el vértice y lo divide en dos ángulos de 30° cada uno.

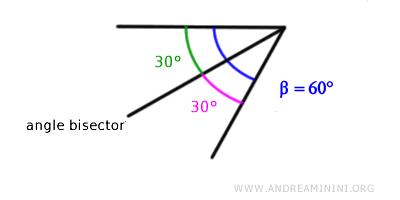
Ecuación de la Bisectriz de un Ángulo

La ecuación que describe las bisectrices de los ángulos formados por la intersección de dos rectas es: $$ \frac{ax+by+c}{ \sqrt{a^2+b^2}} = \pm \frac{a'x+b'y+c'}{ \sqrt{a'^2+b'^2}} $$

Esta ecuación determina las dos bisectrices que dividen un ángulo en dos partes congruentes.

El símbolo ± indica la existencia de dos bisectrices distintas: una correspondiente al ángulo agudo y otra al ángulo obtuso que se forman en la intersección de las dos rectas.

Ejemplo

Consideremos las siguientes ecuaciones de rectas:

$$ r: \ x - y = 0 $$

$$ s: \ x + y - 4 = 0 $$

Se trata de dos rectas que se cortan.

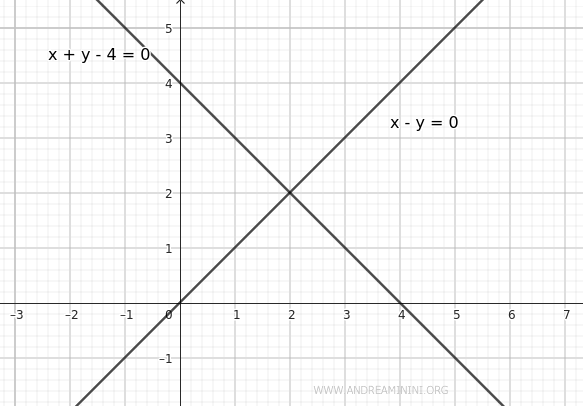
Utilizamos la ecuación general de las bisectrices:

$$ \frac{ax + by + c}{\sqrt{a^2 + b^2}} = \pm \frac{a'x + b'y + c'}{\sqrt{a'^2 + b'^2}} $$

Sustituyamos los coeficientes de ambas rectas: a=1, b=-1, c=0 y a'=1, b'=1, c'=-4

$$ \frac{x - y }{\sqrt{1^2 + (-1)^2}} = \pm \frac{x + y -4}{\sqrt{1^2 + 1^2}} $$

$$ \frac{x - y }{\sqrt{2}} = \pm \frac{x + y -4}{\sqrt{2}} $$

Eliminamos el denominador \(\sqrt{2}\), ya que es el mismo en ambas expresiones:

$$ \frac{x - y }{\sqrt{2}} \cdot \sqrt{2} = \pm \frac{x + y -4}{\sqrt{2}} \cdot \sqrt{2} $$

$$ x - y = \pm ( x + y - 4 ) $$

Ahora separamos los dos casos según el signo:

• Para el signo positivo (+): $$ x - y = x + y - 4 $$ Reordenando términos: $$ -2y = -4 $$ Por tanto, la ecuación de una bisectriz es una recta paralela al eje x: $$ y = 2 $$
• Para el signo negativo (-): $$ x - y = -(x + y - 4) $$ $$ x - y = -x - y + 4 $$ Reordenando términos: $$ 2x = 4 $$ La otra bisectriz es una recta paralela al eje y: $$ x = 2 $$

Por lo tanto, las ecuaciones de las dos bisectrices de los ángulos formados por las rectas son $ y = 2 $ y $ x = 2 $

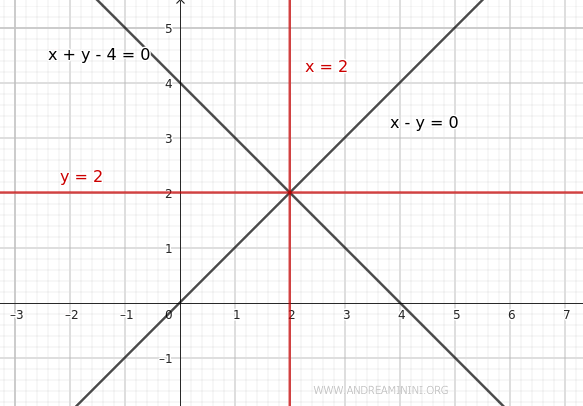
Observaciones

Algunas consideraciones sobre la bisectriz:

• Todo ángulo posee una única bisectriz.
• Dos rectas secantes generan dos pares de ángulos opuestos congruentes y dos bisectrices perpendiculares entre sí.
  Por ejemplo, si dos rectas r y s se cruzan formando un ángulo agudo de 45°, el ángulo opuesto también mide 45°. Como un ángulo llano mide 180°, el ángulo suplementario de 45° es un ángulo obtuso de 135° (180° - 45° = 135°), y su ángulo opuesto también mide 135°.
  
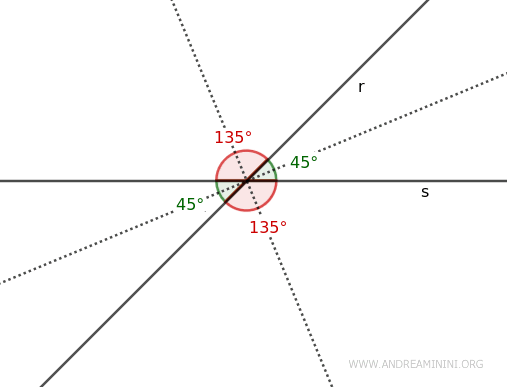
• Dos ángulos opuestos por el vértice comparten la misma bisectriz.
• Todos los puntos situados sobre la bisectriz están a la misma distancia de los lados del ángulo.
  La bisectriz de un ángulo constituye un lugar geométrico, ya que cualquier punto sobre ella equidista de los lados del ángulo.

  Demostración. Tomemos un punto P cualquiera sobre la bisectriz r del ángulo. Dado que la bisectriz divide el ángulo en dos ángulos congruentes α≅α'. Trazamos un segmento OP que une el vértice con el punto P sobre la bisectriz, y dos segmentos perpendiculares AP y BP desde P hasta los lados del ángulo. A partir de esta construcción se deduce que los triángulos OAP y OBP son congruentes según el segundo criterio de congruencia de triángulos, pues tienen dos ángulos congruentes y un lado común (OP). Si los triángulos son congruentes, todos sus lados son congruentes. Por tanto, los segmentos AP ≡ BP son congruentes. Esto demuestra que cualquier punto P sobre la bisectriz está a la misma distancia de los lados del ángulo.
  
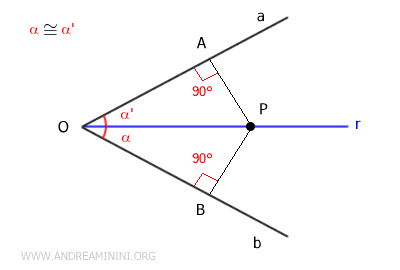
  Demostración recíproca. En este caso, debemos demostrar que todo punto P que equidista de los lados del ángulo se encuentra sobre la bisectriz. Según la hipótesis, consideramos un punto P equidistante de los lados del ángulo, es decir, AP ≡ BP, y la bisectriz r. La distancia de un punto a un lado se mide mediante el segmento perpendicular trazado desde P hasta dicho lado. Por tanto, la distancia AP es perpendicular al lado “a”, mientras que la distancia BP es perpendicular al lado “b”. Los triángulos rectángulos OAP y OBP son congruentes según los criterios de congruencia de triángulos rectángulos, ya que tienen los catetos AP y BP congruentes y la hipotenusa OP también congruente. Al ser congruentes, ambos triángulos tienen lados y ángulos congruentes. En particular, nos interesan los ángulos α ≡ α' de los triángulos OAP y OBP, lo cual indica que la hipotenusa OP y el punto P pertenecen a la bisectriz r del ángulo. Por lo tanto, si un punto P equidista de los lados de un ángulo, se encuentra sobre la bisectriz r de dicho ángulo.

Y así sucesivamente.