Ángulos Suplementarios, Complementarios y Explementarios

Dos ángulos se denominan complementarios, suplementarios o explementarios según si la suma de sus medidas equivale, respectivamente, a un ángulo recto, un ángulo llano o un ángulo completo.

• Ángulos Complementarios

  Dos ángulos son complementarios si la suma de sus medidas es de 90 grados (π/2 radianes).
  

  Dicho en otras palabras, si la suma de dos ángulos forma un ángulo recto, se dice que son complementarios.

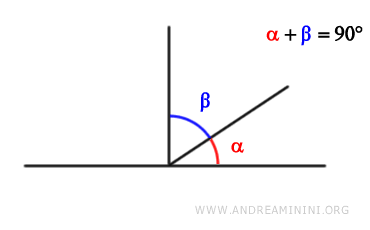
  Por ejemplo, si un ángulo mide 30 grados y el otro 60 grados $$ \alpha=30° $$ $$ \beta=60° $$ se consideran complementarios porque su suma es de 90 grados $$ \alpha+\beta = 30° + 60° = 90° $$.

• Ángulos Suplementarios

  Dos ángulos son suplementarios si la suma de sus medidas es de 180 grados (π radianes).
  

  Es decir, si la suma de dos ángulos forma un ángulo llano, se trata de ángulos suplementarios.

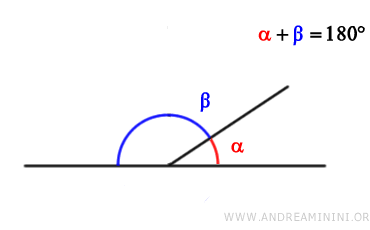
  Por ejemplo, si un ángulo mide 120 grados y el otro 60 grados $$ \alpha=120° $$ $$ \beta=60° $$ son ángulos suplementarios porque su suma es 180 grados $$ \alpha+\beta = 120° + 60° = 180° $$.

• Ángulos Explementarios

  Dos ángulos son explementarios si la suma de sus medidas alcanza los 360 grados (2π radianes).
  

  En pocas palabras, si la suma de dos ángulos completa una circunferencia, se dice que son explementarios.

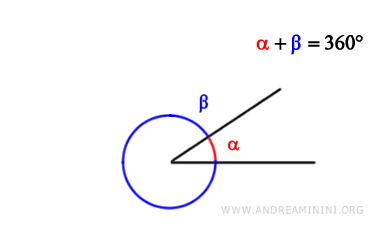
  Por ejemplo, si un ángulo mide 270 grados y el otro 90 grados $$ \alpha=270° $$ $$ \beta=90° $$ se consideran explementarios porque su suma es de 360 grados $$ \alpha+\beta = 270° + 90° = 360° $$.

En resumen, los ángulos complementarios, suplementarios y explementarios se clasifican según la suma de sus medidas: los complementarios suman 90°, los suplementarios 180° y los explementarios 360°.

Estas definiciones se aplican exclusivamente a pares de ángulos.

Por lo tanto, un solo ángulo no puede describirse como suplementario, complementario o explementario si no se lo relaciona con otro ángulo.

Y así sucesivamente.