Ángulos Suplementarios
Ángulos suplementarios son dos ángulos cuya suma es igual a 180° (π radianes).
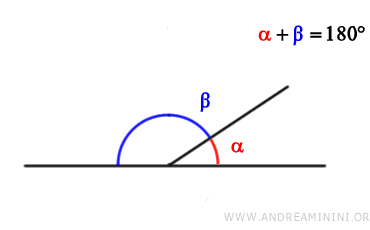
En otras palabras, dos ángulos se consideran «suplementarios» cuando su suma equivale a un ángulo llano.
Esto se cumple sin importar la posición o la orientación de los ángulos.
El concepto de ángulos suplementarios solo tiene sentido aplicado a pares de ángulos. Por tanto, un único ángulo no puede ser suplementario por sí solo: siempre se requieren dos.
Un Ejemplo Práctico
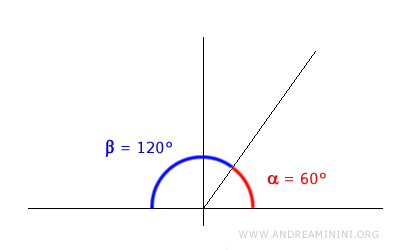
Veamos el siguiente par de ángulos:
$$ \alpha = 60° $$
$$ \beta = 120° $$
Estos ángulos son suplementarios porque la suma de sus medidas es 180°.
$$ \alpha + \beta = 180° $$
El resultado de esta suma es un ángulo llano.
Aspectos Clave
Los ángulos suplementarios presentan propiedades muy interesantes:
- Todo ángulo posee su ángulo suplementario
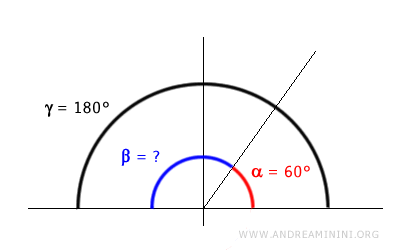
Para cualquier ángulo dado, es posible determinar su ángulo suplementario restando su medida a 180 grados. Por ejemplo, si el ángulo alfa mide 120°: $$ \alpha = 120° $$ entonces su ángulo suplementario beta mide 60°: $$ \beta = 180° - \alpha = 180° - 120° = 60° $$ Así, para cualquier ángulo, siempre se puede hallar su suplemento calculando la diferencia.
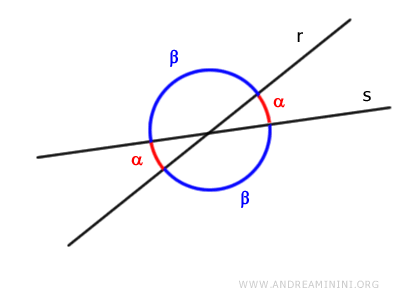
- Cuando dos rectas se cortan, los ángulos consecutivos que se forman por pares son suplementarios
Esta propiedad resulta especialmente útil para resolver problemas geométricos y para demostrar teoremas.
- Los ángulos adyacentes siempre son suplementarios (y viceversa)
Dos ángulos se consideran «adyacentes» cuando comparten un lado y los lados no comunes se prolongan sobre la misma recta. Por lo tanto, para hallar el suplemento de un ángulo basta con identificar su ángulo adyacente.
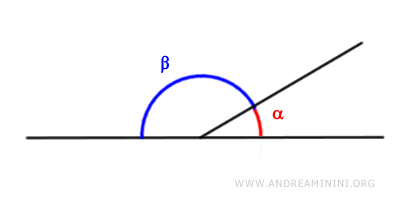
- Ángulos suplementarios de dos ángulos congruentes
Si dos ángulos, \( \alpha \) y \( \alpha' \), son suplementarios de otros dos ángulos congruentes, \( \beta \cong \beta' \) (o del mismo ángulo), entonces también son congruentes entre sí: \( \alpha \cong \alpha' \).
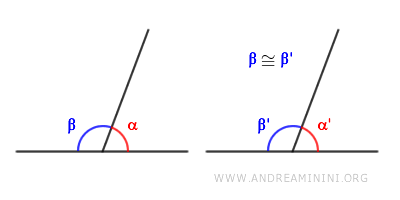
Demostración. Sea \( \alpha \) y \( \alpha' \) dos ángulos, cada uno suplementario de \( \beta \) y \( \beta' \), respectivamente. Por definición: $$ \alpha + \beta = 180^\circ $$ $$ \alpha' + \beta' = 180^\circ $$ Dado que \( \beta \) y \( \beta' \) son congruentes (\( \beta \cong \beta' \)), podemos expresar \( \alpha \) y \( \alpha' \) así: $$ \alpha = 180^\circ - \beta $$ $$ \alpha' = 180^\circ - \beta' $$ Como \( \beta \) y \( \beta' \) tienen la misma medida, sustituimos \( \beta' \) por \( \beta \) en la ecuación: $$ \alpha = 180^\circ - \color{red}{ \beta' } $$ $$ \alpha' = 180^\circ - \beta' $$ Dado que todos los ángulos llanos (180°) son congruentes, y sabiendo que \( \beta \cong \beta' \), se deduce que \( \alpha \) y \( \alpha' \) también son congruentes. Por tanto, concluimos que: $$ \alpha \cong \alpha' $$ como queríamos demostrar.
Y así sucesivamente.