Medición de Ángulos
Medición de ángulos hace referencia al tamaño de la abertura que se forma entre dos líneas o semirrectas, denominadas lados del ángulo, que se encuentran en un punto común llamado vértice.
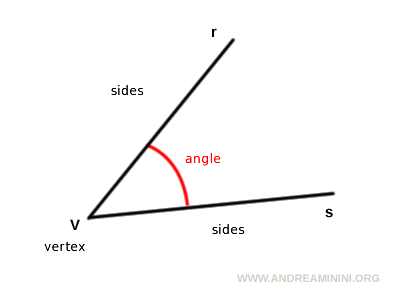
Indica cuán amplio es un ángulo.
Los ángulos se expresan en grados, que varían de 0° a 360°, o en radianes.
Otros significados de medida. En geometría, el término medida suele referirse al tamaño de un ángulo. Sin embargo, también tiene otros usos. En matemáticas, por ejemplo, puede indicar la diferencia entre los valores extremos de un intervalo, clase o conjunto. En ese caso, la medida se refiere a la distancia entre el valor máximo y el mínimo de un conjunto.
Unidades de Medición de Ángulos
La medición de ángulos puede expresarse en diversas unidades, como grados, radianes y vueltas completas.
- Grados
Es la unidad más habitual en geometría plana, donde un círculo completo se divide en 360 grados. Un ángulo llano mide 180°, mientras que un ángulo recto, que es la mitad de uno llano, mide 90 grados.
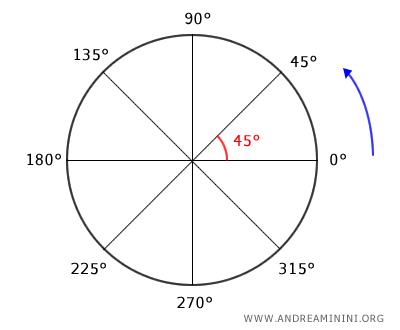
- Radianes
En matemáticas y física, es frecuente medir los ángulos en radianes. Un radián se define como el ángulo que abarca un arco cuya longitud es igual al radio del círculo. Por eso, un círculo completo contiene 2π radianes (aproximadamente 6,283 radianes).
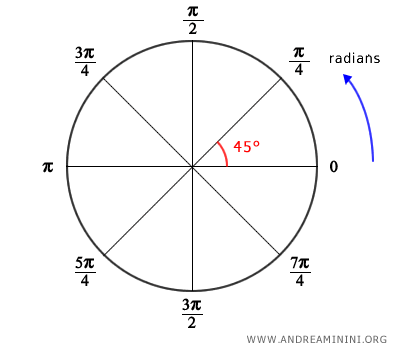
- Vueltas completas
A veces, los ángulos se miden en vueltas completas, donde una vuelta equivale a un círculo entero y media vuelta equivale a un semicírculo. Así, un ángulo llano corresponde a 1/2 vuelta y un ángulo recto a 1/4 de vuelta.
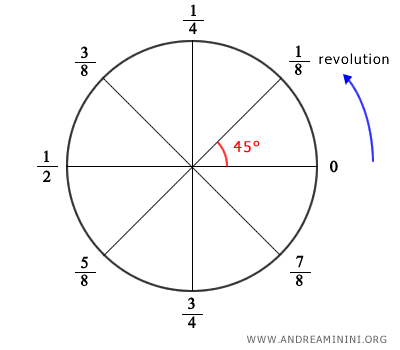
Para compararlas, una vuelta completa equivale a 360 grados y a 2π radianes.
Un Ejemplo Práctico
Para comprender mejor la medición de ángulos, resulta muy útil imaginarse un reloj.
Las agujas de las horas y los minutos actúan como dos lados (semirrectas) que forman ángulos de distintos tamaños.
Por ejemplo, cuando las agujas marcan las 3:00, forman un ángulo recto de 90 grados.

Del mismo modo, un ángulo de 180 grados, llamado ángulo llano, se representa cuando las agujas marcan las 6:00.
Este mide exactamente el doble que el ángulo recto anterior.

Un ángulo de 270 grados se representa cuando las agujas marcan las 9:00, siendo exactamente tres veces mayor que un ángulo recto.

El reloj es uno de los recursos más sencillos y visuales para entender cómo se miden los ángulos.
Da igual el tamaño del reloj, sea pequeño o tan grande como el Big Ben: el ángulo entre sus agujas siempre se mide del mismo modo.
Clases de Equivalencia
Los ángulos que tienen la misma medida se denominan congruentes y pertenecen a la misma clase de equivalencia.
Por ejemplo, dos ángulos de 45 grados pertenecen a la misma clase de equivalencia.
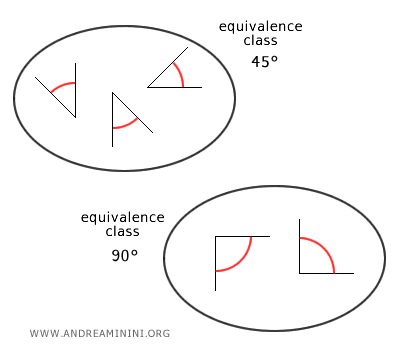
Sin embargo, un ángulo de 45 grados y uno de 90 grados pertenecen a clases de equivalencia distintas.
De esto se deduce que siempre es posible comparar dos ángulos.
Además, la suma de dos ángulos no constituye una operación interna, ya que el resultado puede pertenecer a otra clase de equivalencia.
Por ejemplo, la suma de dos ángulos congruentes de 45 grados da 90 grados, que corresponde a una clase de equivalencia distinta.
Y así sucesivamente.