Comparación de Ángulos

Uno de los métodos clásicos para comparar la amplitud de dos ángulos es el método de superposición.

1. Para comparar dos ángulos, α y β, y determinar si son congruentes:
   
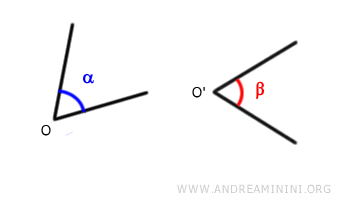
2. Primero, se hace coincidir el vértice O del primer ángulo (α) con el vértice O' del segundo ángulo (β) mediante una traslación:
   
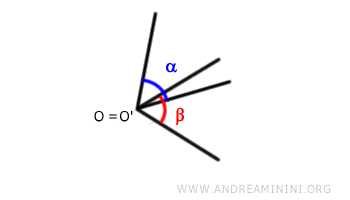
3. Después, se rota uno de los lados del primer ángulo (α) hasta hacerlo coincidir con uno de los lados del segundo ángulo (β):
   
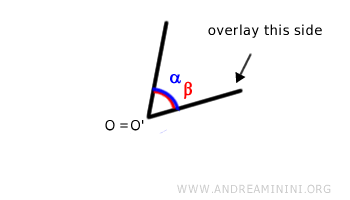
4. Si los otros dos lados también coinciden, los ángulos son congruentes, es decir, tienen la misma amplitud medida en grados o radianes:
   
   

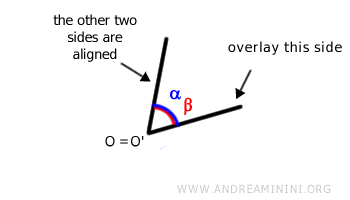
   Por el contrario, si los otros lados no coinciden, los ángulos no son congruentes. En ese caso, uno de ellos es mayor y el otro menor. Se considera que un ángulo es menor si está contenido completamente dentro de la región angular del otro. De lo contrario, es mayor. Por ejemplo, consideremos otros dos ángulos, α y β, y superpongámoslos utilizando el mismo procedimiento explicado antes:
   
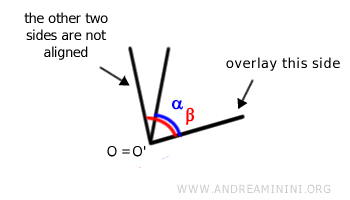
   En este ejemplo, el ángulo α (en azul) está totalmente contenido dentro de la región angular del ángulo β (en rojo). Por tanto, el ángulo α es menor que β. Así, podemos decir que el ángulo α es menor que β o que β es mayor que α.

Diferencia entre Ángulos Congruentes e Iguales

De forma más precisa, en geometría se afirma que dos ángulos son "congruentes" y no simplemente "iguales" cuando pueden superponerse mediante movimientos rígidos, ya que la igualdad implicaría que ambos ángulos coinciden exactamente en los mismos puntos del plano, lo cual no siempre sucede.

La congruencia, en cambio, no exige que dos objetos geométricos ocupen exactamente los mismos puntos en el espacio.

Por ejemplo, dos ángulos α y β pueden tener la misma medida en grados o radianes (por ejemplo, 90°), pero encontrarse situados en posiciones distintas en el espacio. En este caso, no se dice que sean ángulos iguales, sino que son ángulos congruentes α≅β.

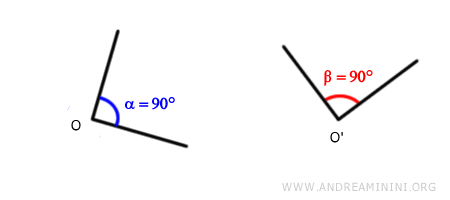
Esto implica que, si bien todos los ángulos iguales son congruentes, no todos los ángulos congruentes son necesariamente iguales.

Nota: Los ángulos congruentes se relacionan con las isometrías, pues pueden superponerse mediante un movimiento rígido.

Otros Métodos para Comparar Ángulos

Existen otros métodos para comparar ángulos en geometría:

• Medición Directa
  Se coloca el centro del transportador sobre el vértice del ángulo (O) y se alinea la base del transportador con uno de los lados del ángulo. De este modo, se puede leer directamente la amplitud del ángulo en la escala graduada del transportador. Por ejemplo, el ángulo α mide 60°.
  
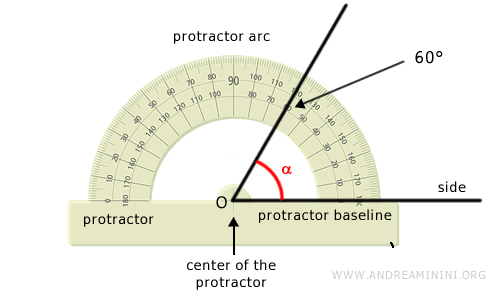
  A continuación, se repite el mismo procedimiento para el ángulo β. Así, es posible comparar las amplitudes de α y β basándose en sus medidas directas en grados o radianes.
• Cálculos Matemáticos
  Si se conocen los vectores que definen los lados de los ángulos, se pueden emplear fórmulas trigonométricas para calcular su amplitud. Por ejemplo, el ángulo entre dos vectores puede determinarse utilizando el producto escalar. Una vez calculadas las medidas, se pueden comparar para establecer si los ángulos son congruentes o no.

En cualquiera de estos métodos, es posible determinar si dos ángulos son congruentes o si uno es mayor o menor que el otro.

Y así sucesivamente.