Vectores

¿Qué es un vector?

Un vector es un concepto matemático fundamental que se define por tres atributos clave: magnitud, dirección y sentido.

En otras palabras, un vector es un segmento al que se le ha asignado una dirección, es decir, un segmento orientado.

Para indicar que es un vector, se suelen denotar los extremos del segmento dirigido colocando una flecha encima (por ejemplo, \( \overrightarrow{AB} \)).

Alternativamente, se puede representar el vector con una letra minúscula con una flecha encima (por ejemplo, \( \vec{v} \)).

El punto inicial del vector se llama ‘punto de aplicación’, mientras que su punto terminal, marcado por la flecha, indica su extremo final.

Observa el segmento de línea de un vector. Este segmento define su dirección, mientras que la flecha indica su sentido.

La longitud del segmento dirigido se llama magnitud y se representa colocando el nombre del vector entre dos barras verticales. Por ejemplo, $ | \vec{v} | \ \ \text{o} \ \ | \overrightarrow{AB} | $

A veces, la magnitud se representa simplemente con el símbolo del vector sin la flecha encima (por ejemplo, \( v \)).

El símbolo del vector \( \vec{v} \) no debe confundirse con su magnitud \( | \vec{v} | \). El símbolo \( \vec{v} \) representa todas las características del vector (dirección, sentido, longitud) y es una cantidad vectorial. La magnitud \( | \vec{v} | \), por su parte, indica solo la longitud y es una cantidad escalar (es decir, un número real). Así, la magnitud \( | \vec{v} | \) es un componente del vector \( \vec{v} \).

¿Por qué son importantes los vectores?

En física, existen cantidades que se definen naturalmente por su magnitud, dirección y sentido.

Ejemplos de estas cantidades son el desplazamiento, la velocidad, la fuerza y la aceleración.

Los vectores se utilizan para representar gráficamente estas cantidades.

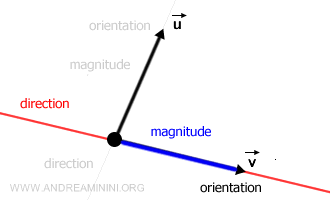
Cada vector se caracteriza de manera única por su dirección, sentido y magnitud.

Para representar visualmente un vector, se emplea un segmento de línea dirigido, que se interpreta de esta forma:

• La orientación de la flecha indica el sentido del vector.
• La longitud de la flecha, también llamada magnitud o norma, mide su intensidad y es de naturaleza escalar.
• La línea sobre la que se dibuja la flecha proporciona información sobre la dirección del vector.

Distinguir entre un vector y su magnitud. Es esencial diferenciar entre un vector y su magnitud. Confundir uno con el otro es un error común que puede llevar a malentendidos importantes. Mientras que un vector engloba magnitud, dirección y sentido, su magnitud es simplemente un valor escalar que representa únicamente su longitud. Para mayor claridad, dos vectores pueden tener la misma magnitud pero diferenciarse por sus direcciones y sentidos.

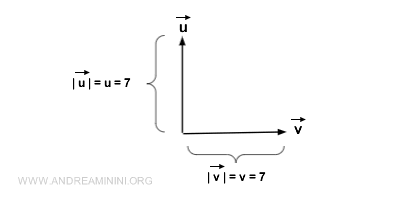
De manera convencional, la magnitud se representa con el símbolo del vector, sin la flecha, o encerrando el símbolo entre barras verticales. En cambio, los vectores suelen denotarse con una flecha sobre la letra o usando la letra en negrita.

Aunque los vectores abarcan un campo matemático extenso, el concepto básico sigue siendo el mismo.

Operaciones con vectores

Los vectores admiten dos operaciones principales:

• Suma de vectores
  La suma de dos vectores da como resultado un tercer vector.
  
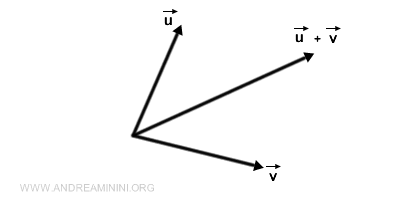
• Multiplicación por un escalar
  Multiplicar un vector por un escalar (por ejemplo, dos) da como resultado un vector con una magnitud ajustada proporcionalmente, pero que conserva su dirección y sentido originales.
  

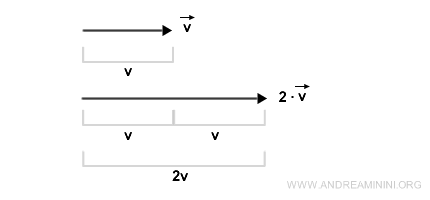
En ambos casos, las operaciones generan otro vector como resultado.

¿Qué es un vector?

Los vectores son conceptos fundamentales en matemáticas y física. Para empezar a comprenderlos, observaremos primero los vectores en un plano bidimensional, lo cual facilita su interpretación.

En un espacio bidimensional, específicamente en el plano x,y, un vector se define como un segmento dirigido. Este segmento tiene tres características principales: su magnitud (o longitud), su dirección y su sentido.

Observa esta ilustración:

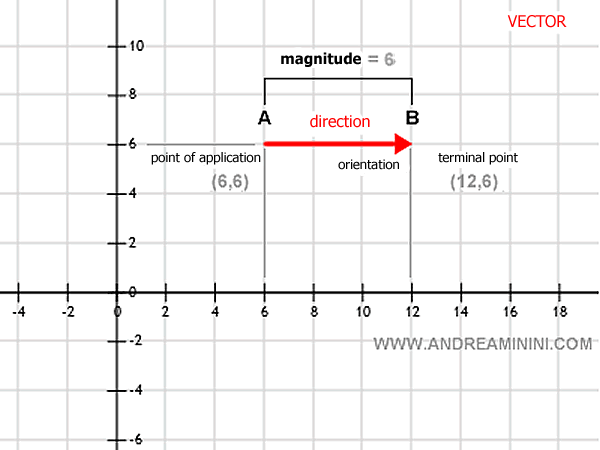
Ejemplo. Imagina un segmento en un plano que mide 6 unidades, comenzando en el punto A (6,6) y terminando en el punto B (12,6). Al asignarle una dirección de A a B, hemos definido un vector.

En matemáticas y física, los vectores se suelen denotar utilizando los puntos inicial y terminal con una flecha encima:

$$ \overrightarrow{AB} $$

También pueden representarse de manera más breve como:

$$ AB $$

Diferenciando vectores aplicados y libres

Vectores aplicados

Un vector aplicado tiene un punto inicial específico, conocido como su punto de aplicación.

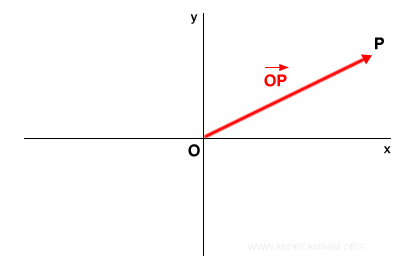
Por ejemplo, si tenemos un punto P y un origen O en el plano, el vector que comienza en O y termina en P se representa como el par de puntos OP. Esto se puede denotar como: $$ \overrightarrow{OP} $$ o usando letras minúsculas como v, u, w, etc.

Para ilustrarlo:

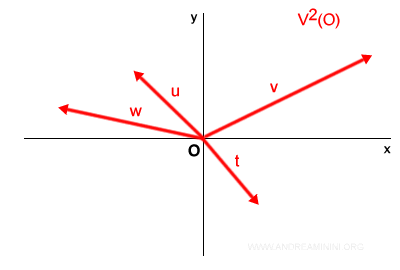
Todos los vectores que comparten un punto inicial común, como O, pueden agruparse y representarse como:

$$ V^2(O) $$

Para una representación práctica:

Es importante notar que, aunque O representa el origen del plano, el punto inicial del vector puede ser otro.

Por ejemplo, el segmento dirigido AB tiene su punto inicial en A.

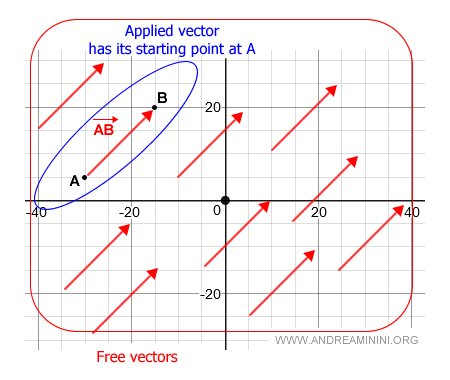
Vectores libres

En cambio, un vector libre no tiene un punto de inicio fijo. Solo se define por su dirección y magnitud.

Todos estos vectores en un plano se representan colectivamente como:

$$ V $$

Nota. Un vector libre agrupa esencialmente todos los vectores que pertenecen a una misma clase de equivalencia, actuando como representante de esa clase.

Definición de un vector en matemáticas

Un vector es un elemento de un espacio vectorial. En el contexto de los espacios vectoriales reales, un vector es un n-upla ordenada de números reales ( x₁, ... , x_n ).

A estos números reales que componen el vector se les llama sus componentes.

Un Ejemplo Práctico

A continuación, algunos ejemplos de vectores de dos componentes (n=2) en el campo de los números reales:

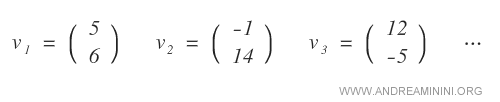
La colección de todos los vectores con dos componentes constituye el espacio vectorial real ( R² = RxR ).

Este espacio ( R² ) corresponde a todos los puntos en el plano cartesiano.

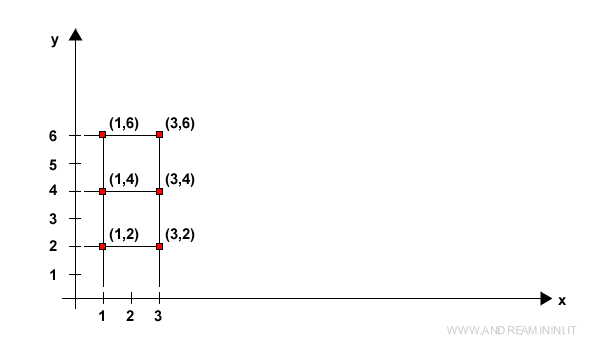
En efecto, cada par de números reales ( x₁, x₂ ) corresponde a un punto único ( x, y ) en el plano cartesiano.

Suma de vectores

Si tenemos dos vectores numéricos cada uno con n componentes:

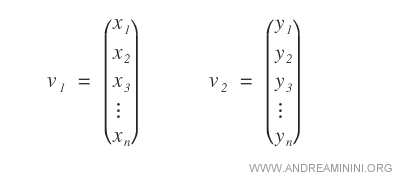
La suma de estos vectores da como resultado un vector con n componentes, donde cada componente ( z_n ) es la suma de los componentes correspondientes ( x_n + y_n ).

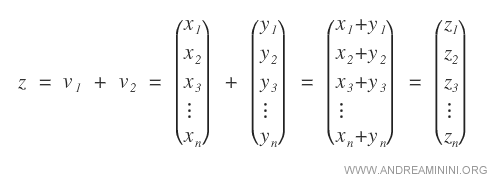
Multiplicación escalar de un vector

Si tenemos un vector v con n componentes y un escalar real cualquiera α, el producto del vector por el escalar da como resultado un vector donde cada componente x_n se multiplica por el escalar α.

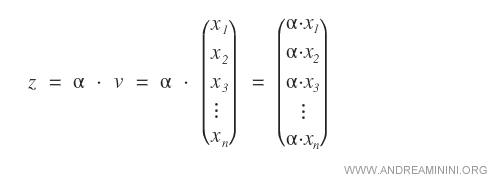
Representación de un vector

En un espacio bidimensional, los vectores pueden representarse en el plano cartesiano.

Dos vectores geométricos OE₁ y OE₂ son linealmente independientes si están en líneas distintas que pasan por el origen.

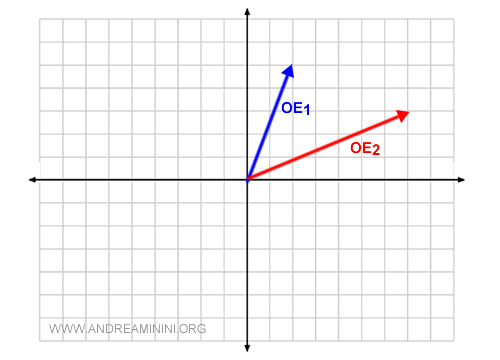
Dos vectores independientes forman una base para el espacio vectorial V²O, ya que su combinación lineal puede generar todos los vectores libres en el espacio vectorial bidimensional V².

$$ B = \{ OE_1 , OE_2 \} $$

Cada punto P en el plano corresponde a un vector numérico v(x,y) que identifica las coordenadas C_v(x,y) del vector OP en relación con la base { OE₁, OE₂ }.

$$ OP = a_1 \cdot OE1 + a_2 \cdot OE2 $$

Inversamente, cada vector v(x,y) corresponde a un punto P en el plano mediante combinación lineal.

Un ejemplo práctico

Utilizo los vectores v₁=(0,1) y v₂(1,0) como base de vectores B, que son OE₁ y OE₂ respectivamente.

$$ B = \{ v_1 , v_2 \} \\ v_1 = \begin{pmatrix} x \\ y \end{pmatrix} =\begin{pmatrix} 0 \\ 1 \end{pmatrix} \\ v_2 = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} $$

Además de ser linealmente independientes, v₁ y v₂ también son ortogonales entre sí, lo que facilita la representación gráfica.

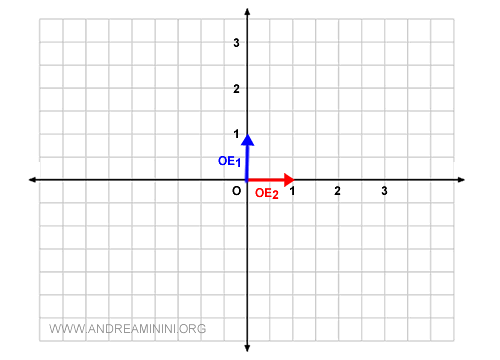
Ahora, quiero representar el punto P en el gráfico.

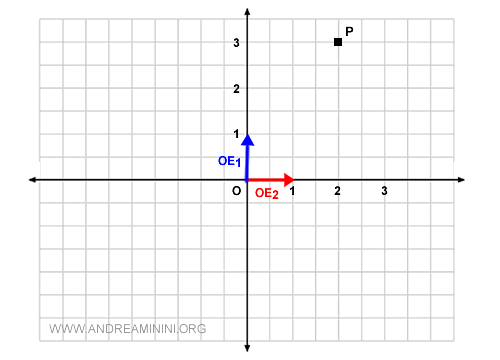
Como cada punto en el plano, el punto P corresponde a un vector que pasa por el origen (O).

En este caso, es el vector geométrico OP.

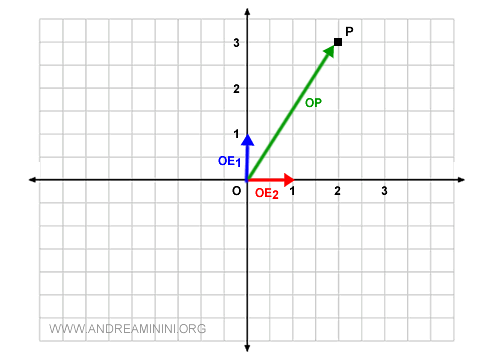
El vector \( OP \) es linealmente dependiente de los vectores base { OE₁, OE₂ } ya que puede representarse mediante su combinación lineal.

En esencia, existen dos escalares c₁ y c₂, conocidos como coordenadas, tales que:

$$ \overrightarrow{OP} = c_1 OE_1 + c_2OE_2$$

$$ \overrightarrow{OP} = c_1 \begin {pmatrix} 0 \\ 1 \end{pmatrix} + c_2 \begin {pmatrix} 1 \\ 0 \end{pmatrix} $$

$$ \overrightarrow{OP} = 3 \begin {pmatrix} 0 \\ 1 \end{pmatrix} + 2 \begin {pmatrix} 1 \\ 0 \end{pmatrix} $$

$$ \overrightarrow{OP} = \begin {pmatrix} 0 \\ 3 \end{pmatrix} + \begin {pmatrix} 2 \\ 0 \end{pmatrix} $$

$$ \overrightarrow{OP} = \begin {pmatrix} 2 \\ 3 \end{pmatrix} $$

En este caso, la solución es sencilla.

Las coordenadas son c₁=3 y c₂=2, es decir, tres veces el vector OE₁ y dos veces el vector OE₂.

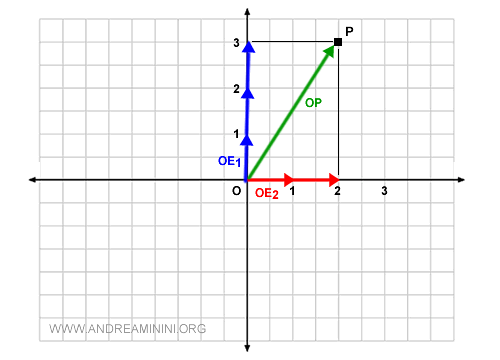
La correspondencia entre el punto P y el vector OP se denota mediante la siguiente relación de equivalencia:

$$ \overrightarrow{OP} \equiv P \begin{pmatrix} 2 \\ 3 \end{pmatrix} $$

De manera similar, puedo representar cualquier otro punto en el plano cartesiano R x R o R².

Nota. La correspondencia entre puntos y vectores es invaluable, ya que nos permite estudiar las propiedades geométricas de puntos y vectores usando el álgebra lineal.

Vectores en espacios multidimensionales

En matemáticas, los vectores no se limitan al plano bidimensional que solemos visualizar. Pueden existir y definirse en espacios multidimensionales.

Vectores en dos dimensiones

En un espacio bidimensional, denotado como R², un vector se caracteriza por la diferencia entre sus puntos inicial y terminal en un plano.

$$ V \{ x_2-x_1, y_2-y_1 \} $$

Ejemplo

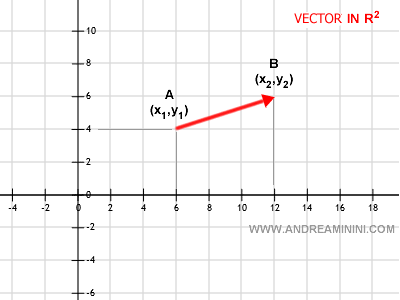
Considera, por ejemplo, un vector en el plano: $$ V \{ x_2-x_1, y_2-y_1 \} $$ Desglosando: $$ V \{ 12-6, 6-4 \} $$ Obtenemos: $$ V \{ 6, 2 \} $$

Vectores en tres dimensiones

Al pasar a un espacio tridimensional, o R³, la representación sigue siendo algebraicamente consistente, pero con una coordenada adicional en z.

$$ V \{ x_2-x_1, y_2-y_1, z_2-z_1 \} $$

De forma abreviada, los elementos del vector pueden expresar directamente la diferencia, a veces referida como aceleración.

$$ V \{ x, y, z \} $$

Donde:

$$ x=x_2-x_1 $$ $$ y=y_2-y_1 $$ $$ z=z_2-z_1 $$

Esta notación es especialmente útil en dimensiones superiores.

Ejemplo

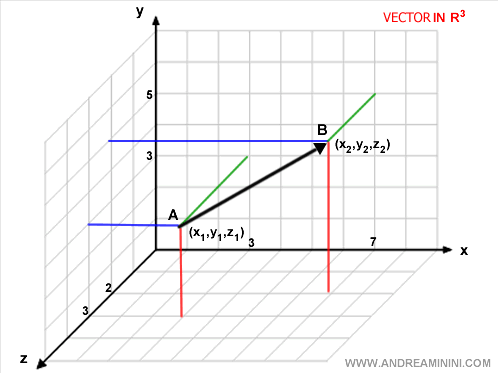
Considera un vector en un espacio 3D (x,y,z): $$ V \{ x_2-x_1, y_2-y_1, z_2-z_1 \} $$ Dados los puntos A=(3,3,3) y B=(7,5,2): $$ con A=(3,3,3) , B=(7,5,2) $$ $$ V \{ 7-3, 5-3, 2-3 \} $$ Esto resulta en: $$ V \{ 4, 2, -1 \} $$

Vectores en n dimensiones

Extendiendo el concepto a espacios n-dimensionales, representados como Rⁿ, tenemos:

$$ V \{ x_1, x_2, x_2, ... , x_n \} $$

Sin embargo, visualizar estos vectores geométricamente plantea un desafío.

Nuestra experiencia está arraigada en tres dimensiones, y solemos considerar la cuarta como el tiempo. Más allá de esto, nuestra capacidad para visualizar dimensiones superiores se limita. Esto no es una deficiencia, sino una muestra de la complejidad del mundo matemático. Para explorar estas dimensiones complejas, solemos emplear simplificaciones o métodos alternativos de representación.

Así, los vectores n-dimensionales se representan generalmente como una n-upla ordenada de n elementos:

$$ V \{ x_1, x_2, x_2, ... , x_n \} $$

Donde cada elemento, desde x₁ hasta x_n, puede ser cualquier número real.

Por ejemplo

$$ V \{ 4, 2, -1, 7 , 3 \} $$

La exploración de vectores multidimensionales es fundamental en el álgebra lineal.