Producto vectorial

El producto vectorial en el espacio tridimensional

El producto vectorial es una operación específica entre dos vectores que genera un tercer vector como resultado. Cuando nos referimos al "vector \( \vec{u} \) cruz vector \( \vec{v} \)", lo expresamos así: $$ \vec{u} \times \vec{v} = \vec{w} $$ De forma alternativa, también puede representarse como: $$ \vec{u} \wedge \vec{v} = \vec{w} $$ El módulo de este producto vectorial viene dado por: $$ |\vec{w}| = |\vec{u}| \cdot |\vec{v}| \cdot \sin \alpha_{uv} $$

El producto vectorial se define para dos vectores en el espacio euclídeo \( \mathbb{R}^3 \) y da lugar a un tercer vector.

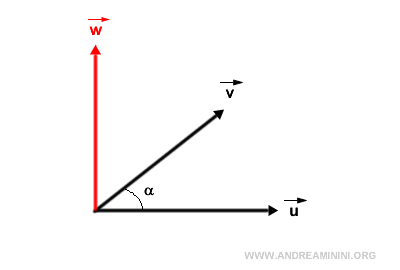
El vector resultante \( \vec{w} \) es ortogonal a los dos vectores originales, es decir, es perpendicular a ambos.

Por convención, el producto vectorial se representa con el símbolo "\times", aunque en algunos contextos también puede utilizarse el símbolo "\wedge".

Propiedades del producto vectorial. Es fundamental conocer las principales propiedades del producto vectorial, ya que constituyen la base del álgebra vectorial.

Propiedades geométricas del producto vectorial

El vector \( \vec{w} \) resultante del producto vectorial presenta las siguientes características:

• El módulo del producto vectorial, es decir, \( |\vec{w}| \), corresponde al área del paralelogramo definido por los vectores \( \vec{u} \) y \( \vec{v} \).
  
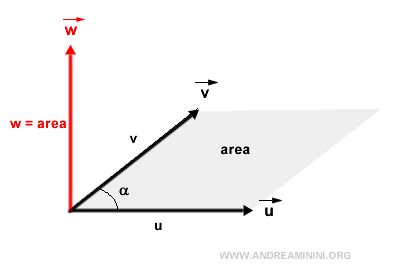
  Desde el punto de vista trigonométrico, el módulo de \( \vec{w} \) se calcula como el producto de los módulos de \( \vec{u} \) y \( \vec{v} \), multiplicado por el seno del ángulo \( \alpha_{uv} \) que forman entre sí. Matemáticamente: $$ |\vec{w}| = |\vec{u}| \cdot |\vec{v}| \cdot \sin \alpha_{uv} $$ Puede interpretarse como el producto de \( |\vec{u}| \) por la componente de \( \vec{v} \) perpendicular a \( \vec{u} \).

  Observación. De esta relación se derivan propiedades muy interesantes. Si los vectores son colineales, su producto vectorial es nulo, ya que el área que abarcan es cero. En particular, si los vectores son paralelos (ángulo de 0°) o antiparalelos (ángulo de 180°), el producto vectorial es el vector nulo.
  
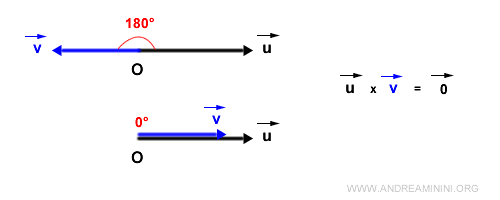
  Si los vectores son ortogonales (ángulo de 90°), el módulo del producto vectorial es simplemente el producto de sus módulos, ya que \( \sin 90^\circ = 1 \).
  
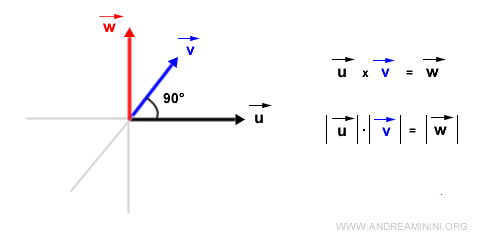
  Si los vectores forman un ángulo de -90°, el módulo del producto vectorial sigue siendo el mismo, pero la dirección del vector \( \vec{w} \) se invierte, ya que \( \sin(-90^\circ) = -1 \).
  

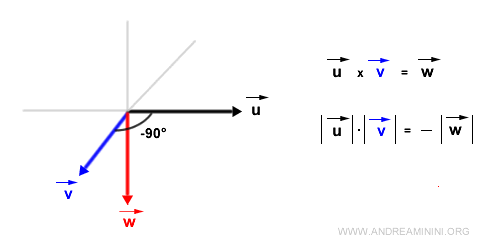
• Dirección del producto vectorial. El vector \( \vec{w} \) es perpendicular al plano definido por los vectores \( \vec{u} \) y \( \vec{v} \).
  
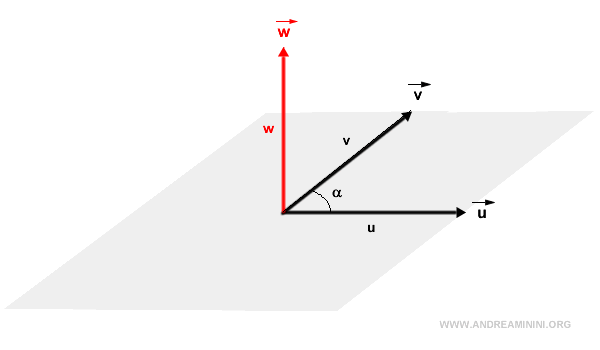
• Para determinar el sentido del vector \( \vec{w} \), se utiliza la regla de la mano derecha. El pulgar representa \( \vec{u} \), el dedo índice representa \( \vec{v} \), y el dedo medio indica la dirección de \( \vec{w} \).
  
  

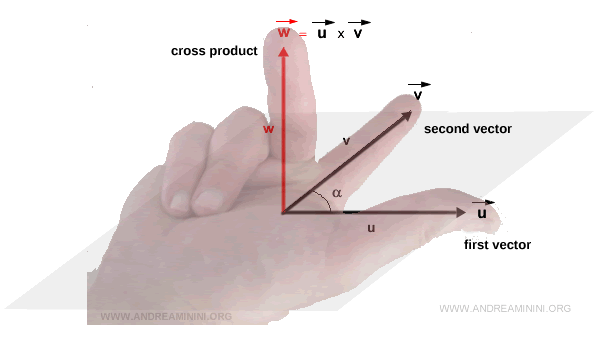
  Observación. Es importante que el pulgar apunte siempre en la dirección del primer vector del producto y el dedo índice en la dirección del segundo.

  Otra forma de determinar la dirección
  Primero se identifica el plano que contiene ambos vectores. Si, observando el plano desde arriba, la rotación más directa para alinear \( \vec{u} \) con \( \vec{v} \) es en sentido antihorario, entonces el vector \( \vec{w} = \vec{u} \times \vec{v} \) apunta hacia arriba. Este principio se conoce como la regla del tornillo de la mano derecha.
  
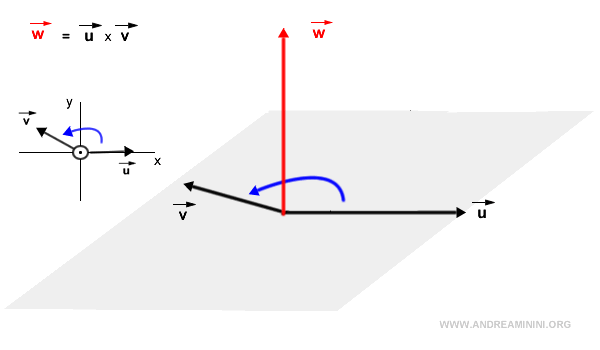
  Por el contrario, si la rotación más directa es en sentido horario, el vector \( \vec{w} \) apunta hacia abajo, es decir, en la dirección opuesta al plano desde el punto de vista del observador.
  
  

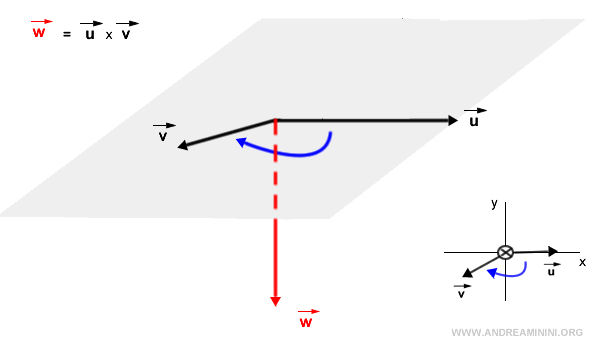
  Observación. De forma general, si se observa desde la punta del vector \( \vec{w} = \vec{u} \times \vec{v} \) mirando hacia el plano, la rotación más directa para llevar \( \vec{u} \) hacia \( \vec{v} \) será siempre en sentido antihorario.

Cálculo del producto vectorial

El producto vectorial puede calcularse mediante dos métodos distintos.

Método 1:

Dado los siguientes vectores:

$$ \vec{v_1} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} $$

y

$$ \vec{v_2} = \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} $$

Su producto vectorial es:

$$ \vec{v_1} \wedge \vec{v_2} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \cdot \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = \begin{pmatrix} det \begin{pmatrix} y_1 & y_2 \\ z_1 & z_2 \end{pmatrix} \\ - det \begin{pmatrix} x_1 & x_2 \\ z_1 & z_2 \end{pmatrix} \\ det \begin{pmatrix} x_1 & x_2 \\ y_1 & y_2 \end{pmatrix} \end{pmatrix} $$

Método 2:

El producto vectorial también puede expresarse como:

$$ \vec{v_1} \wedge \vec{v_2} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \cdot \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} = det \begin{pmatrix} \vec{i} & x_1 & x_2 \\ \vec{j} & y_1 & y_2 \\ \vec{k} & z_1 & z_2 \end{pmatrix} $$

Ejemplo práctico

En el espacio tridimensional \( \mathbb{R}^3 \), consideremos los siguientes vectores:

$$ \vec{v_1} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} $$

$$ \vec{v_2} = \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} $$

Vamos a calcular el producto vectorial \( \vec{v_1} \times \vec{v_2} \) empleando ambos métodos.

Método 1

$$ \vec{v_1} \wedge \vec{v_2} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} = \begin{pmatrix} det \begin{pmatrix} 2 & -3 \\ 1 & 2 \end{pmatrix} \\ - det \begin{pmatrix} 1 & 1 \\ 1 & 2 \end{pmatrix} \\ det \begin{pmatrix} 1 & 1 \\ 2 & -3 \end{pmatrix} \end{pmatrix} $$

Desarrollando los determinantes:

$$ \vec{v_1} \wedge \vec{v_2} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} = \begin{pmatrix} 2 \cdot 2 - (-3) \cdot 1 \\ - \left(1 \cdot 2 - 1 \cdot 1\right) \\ 1 \cdot (-3) - 1 \cdot 2 \end{pmatrix} = \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix} $$

El resultado es un vector ortogonal a ambos vectores originales, es decir, forma un ángulo de 90° con cada uno de ellos.

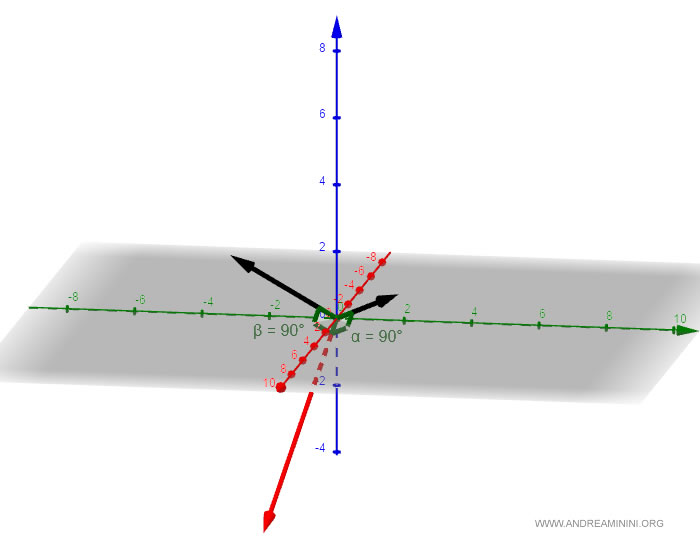
El producto escalar entre dos vectores ortogonales es igual a cero. $$ \left\langle \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix} , \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \right\rangle = 7 \cdot 1 + (-1) \cdot 2 + (-5) \cdot 1 = 7 -2 -5 = 0 $$ $$ \left\langle \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix} , \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} \right\rangle = 7 \cdot 1 + (-1) \cdot (-3) + (-5) \cdot 2 = 7 + 3 -10 = 0 $$ Esto confirma que el vector resultante es efectivamente ortogonal a los vectores originales.

Método 2

Partimos de la siguiente expresión:

$$ \vec{v_1} \wedge \vec{v_2} = \begin{pmatrix} 1 \\ 2 \\ 1 \end{pmatrix} \cdot \begin{pmatrix} 1 \\ -3 \\ 2 \end{pmatrix} = det \begin{pmatrix} \vec{i} & 1 & 1 \\ \vec{j} & 2 & -3 \\ \vec{k} & 1 & 2 \end{pmatrix} $$

Al desarrollar este determinante obtenemos:

$$ \vec{v_1} \wedge \vec{v_2} = \vec{i} \, det \begin{pmatrix} 2 & -3 \\ 1 & 2 \end{pmatrix} - \vec{j} \, det \begin{pmatrix} 1 & 1 \\ 1 & 2 \end{pmatrix} + \vec{k} \, det \begin{pmatrix} 1 & 1 \\ 2 & -3 \end{pmatrix} $$

$$ \vec{v_1} \wedge \vec{v_2} = 7 \vec{i} - \vec{j} - 5 \vec{k} $$

Los coeficientes de los vectores unitarios \( \vec{i} \), \( \vec{j} \) y \( \vec{k} \) representan el resultado del producto vectorial:

$$ \vec{v_1} \wedge \vec{v_2} = \begin{pmatrix} 7 \\ -1 \\ -5 \end{pmatrix} $$

Este resultado coincide perfectamente con el obtenido mediante el Método 1.

Propiedades del producto vectorial

El producto vectorial, denotado \( \vec{a} \times \vec{b} \), presenta varias propiedades fundamentales:

Anticonmutatividad
El producto vectorial no es conmutativo: $$ \vec{a} \wedge \vec{b} = -\vec{b} \wedge \vec{a} $$
Distributividad respecto de la suma vectorial
$$ \vec{a} \wedge (\vec{b} + \vec{c}) = (\vec{a} \wedge \vec{b}) + (\vec{a} \wedge \vec{c}) $$

Otras propiedades relevantes del producto vectorial:

$$ k \cdot \vec{a} \wedge \vec{b} = \vec{a} \wedge (k \cdot \vec{b}) = k \cdot (\vec{a} \wedge \vec{b}) $$ $$ \left\langle \vec{a}, \vec{a} \wedge \vec{b} \right\rangle = \left\langle \vec{b}, \vec{a} \wedge \vec{b} \right\rangle = 0 $$ $$ \| \vec{a} \wedge \vec{b} \|^2 = \| \vec{a} \|^2 \cdot \| \vec{b} \|^2 - \left\langle \vec{a}, \vec{b} \right\rangle^2 $$ $$ \| \vec{a} \wedge \vec{b} \| = \| \vec{a} \| \cdot \| \vec{b} \| \cdot \sin(\widehat{ \vec{a}, \vec{b} }) $$

A estas propiedades podemos añadir otra que resulta particularmente útil para determinar si dos vectores son paralelos.

Dos vectores son linealmente dependientes si su producto vectorial es nulo: $$ \vec{a} \wedge \vec{b} = 0 \ \ \Rightarrow \ \ \vec{a} || \vec{b} $$

El producto vectorial es igual a cero en los siguientes casos:

• Si al menos uno de los vectores es el vector nulo: $$ \vec{a} \wedge \vec{b} = 0 \ \ \text{si} \ \ \vec{a} = \vec{0} \ \ \text{y/o} \ \ \vec{b} = \vec{0} $$
• Si los vectores son paralelos o coinciden, es decir, si son linealmente dependientes: $$ \vec{a} \wedge \vec{b} = 0 \ \ \Rightarrow \ \ \vec{a} || \vec{b} $$

Por tanto, si ninguno de los vectores es nulo, un producto vectorial igual a cero indica que los vectores son linealmente dependientes, es decir, paralelos o coincidentes.

El producto vectorial no es asociativo. El producto vectorial no satisface la propiedad asociativa. Por tanto, el orden en que se realizan los productos es esencial: $$ \vec{a} \wedge (\vec{b} \wedge \vec{c}) \ne (\vec{a} \wedge \vec{b}) \wedge \vec{c} $$

Producto vectorial triple

El producto vectorial triple es una operación vectorial particular en la que uno de los factores es, a su vez, un producto vectorial. Se representa de la siguiente forma: $$ \vec{a} \wedge ( \vec{b} \wedge \vec{c} ) $$

Es fundamental utilizar paréntesis en esta operación, ya que el producto vectorial no es asociativo. Por tanto, se cumple que:

$$ \vec{a} \wedge ( \vec{b} \wedge \vec{c} ) \ne ( \vec{a} \wedge \vec{b} ) \wedge \vec{c} $$

El producto vectorial triple puede desarrollarse utilizando la fórmula de Lagrange: $$ \vec{a} \wedge ( \vec{b} \wedge \vec{c} ) = ( \vec{a} \cdot \vec{c} ) \vec{b} - ( \vec{a} \cdot \vec{b} ) \vec{c} $$ De forma equivalente: $$ \vec{a} \wedge ( \vec{b} \wedge \vec{c} ) = \vec{b} ( \vec{a} \cdot \vec{c} ) - \vec{c} ( \vec{a} \cdot \vec{b} ) $$ Aunque en el miembro izquierdo de la expresión aparece un producto vectorial, en el desarrollo final intervienen únicamente productos escalares. Sin embargo, el resultado sigue siendo un vector. Un recurso mnemotécnico útil para recordar esta fórmula es: ACB - ABC o BAC - CAB.

Ejemplo

Consideremos los siguientes tres vectores:

$$ \vec{a} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} $$

$$ \vec{b} = \begin{pmatrix} 3 \\ 4 \\ 5 \end{pmatrix} $$

$$ \vec{c} = \begin{pmatrix} 6 \\ 7 \\ 8 \end{pmatrix} $$

Para calcular el producto vectorial triple \( \vec{a} \wedge (\vec{b} \wedge \vec{c}) \), comenzamos resolviendo el producto vectorial interno:

$$ \vec{a} \wedge ( \vec{b} \wedge \vec{c} ) $$

$$ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \wedge \left( \begin{pmatrix} 3 \\ 4 \\ 5 \end{pmatrix} \wedge \begin{pmatrix} 6 \\ 7 \\ 8 \end{pmatrix} \right ) $$

El producto vectorial interno es:

$$ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \wedge \begin{pmatrix} det \begin{pmatrix} 4 & 7 \\ 5 & 8 \end{pmatrix} \\ - det \begin{pmatrix} 3 & 6 \\ 5 & 8 \end{pmatrix} \\ det \begin{pmatrix} 3 & 6 \\ 4 & 7 \end{pmatrix} \end{pmatrix} $$

$$ \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} \wedge \begin{pmatrix} -3 \\ 6 \\ -3 \end{pmatrix} $$

Por último, calculamos el producto vectorial externo:

$$ \begin{pmatrix} det \begin{pmatrix} 2 & 6 \\ 3 & -3 \end{pmatrix} \\ - det \begin{pmatrix} 1 & -3 \\ 3 & -3 \end{pmatrix} \\ det \begin{pmatrix} 1 & -3 \\ 2 & 6 \end{pmatrix} \end{pmatrix} $$

$$ \begin{pmatrix} -24 \\ -6 \\ 12 \end{pmatrix} $$

Producto vectorial entre los ejes cartesianos

El producto vectorial entre los ejes cartesianos se define de la siguiente manera:

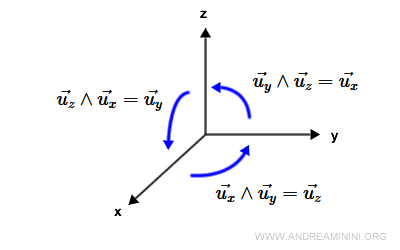
Considerando también los vectores unitarios en sentido opuesto, se obtiene:

$$ \vec{u_x} \wedge \vec{u_y} = \vec{u_z} $$

$$ \vec{u_y} \wedge \vec{u_x} = -\vec{u_z} $$

$$ \vec{u_y} \wedge \vec{u_z} = \vec{u_x} $$

$$ \vec{u_z} \wedge \vec{u_y} = -\vec{u_x} $$

$$ \vec{u_z} \wedge \vec{u_x} = \vec{u_y} $$

$$ \vec{u_x} \wedge \vec{u_z} = -\vec{u_y} $$

Es importante señalar que el producto vectorial de un vector unitario consigo mismo siempre es nulo:

$$ \vec{u_x} \wedge \vec{u_x} = \vec{0} $$

$$ \vec{u_y} \wedge \vec{u_y} = \vec{0} $$

$$ \vec{u_z} \wedge \vec{u_z} = \vec{0} $$

Fórmula alternativa del producto vectorial

En el espacio \( \mathbb{R}^3 \), el producto vectorial de dos vectores se puede expresar como: $$ \vec{a} \wedge \vec{b} = (a_y b_z - a_z b_y ) \vec{u_x} + (a_z b_x - a_x b_z) \vec{u_y} + (a_x b_y - a_y b_x) \vec{u_z} $$

Esta fórmula es especialmente útil cuando se desea calcular el producto vectorial a partir de las componentes de los vectores.

¿Cómo recordar esta fórmula? No siempre es sencillo memorizarla. Afortunadamente, existe un truco práctico para deducirla con rapidez: basta con construir una tabla donde se ubiquen los vectores unitarios en la primera fila, las componentes del primer vector \( \vec{a} \) en la segunda, y las del segundo vector \( \vec{b} \) en la tercera: $$ \begin{pmatrix} u_x & u_y & u_z \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{pmatrix} $$ A continuación, se calcula el determinante de esta matriz aplicando la regla de Sarrus: $$ u_x a_y b_z + u_y a_z b_x + u_z a_x b_y - u_z a_y b_x - u_x a_z b_y - u_y a_x b_z $$ Finalmente, agrupamos los términos con los correspondientes vectores unitarios: $$ (a_y b_z - a_z b_y ) \vec{u_x} + (a_z b_x - a_x b_z ) \vec{u_y} + (a_x b_y - a_y b_x ) \vec{u_z} $$

Demostración de la fórmula

Consideremos el producto vectorial de dos vectores en \( \mathbb{R}^3 \):

$$ \vec{a} \wedge \vec{b} $$

Cada vector se puede expresar como la suma de sus componentes en los tres ejes:

$$ \vec{a} = a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z} $$

$$ \vec{b} = b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} $$

Por lo tanto, el producto vectorial se desarrolla como:

$$ \vec{a} \wedge \vec{b} = ( a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z} ) \wedge ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) $$

Aplicando la propiedad distributiva sobre la suma:

$$ a_x \vec{u_x} \wedge ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) + $$

$$ a_y \vec{u_y} \wedge ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) + $$

$$ a_z \vec{u_z} \wedge ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) $$

Desarrollando cada uno de estos términos:

$$ a_x b_y ( \vec{u_x} \wedge \vec{u_y} ) + a_x b_z ( \vec{u_x} \wedge \vec{u_z} ) + $$

$$ a_y b_x ( \vec{u_y} \wedge \vec{u_x} ) + a_y b_z ( \vec{u_y} \wedge \vec{u_z} ) + $$

$$ a_z b_x ( \vec{u_z} \wedge \vec{u_x} ) + a_z b_y ( \vec{u_z} \wedge \vec{u_y} ) $$

Utilizando las identidades fundamentales:

$$ \vec{u_x} \wedge \vec{u_y} = \vec{u_z}, \quad \vec{u_y} \wedge \vec{u_x} = -\vec{u_z}, $$

$$ \vec{u_y} \wedge \vec{u_z} = \vec{u_x}, \quad \vec{u_z} \wedge \vec{u_y} = -\vec{u_x}, $$

$$ \vec{u_z} \wedge \vec{u_x} = \vec{u_y}, \quad \vec{u_x} \wedge \vec{u_z} = -\vec{u_y} $$

Reuniendo los términos:

$$ a_x b_y \vec{u_z} - a_x b_z \vec{u_y} - a_y b_x \vec{u_z} + a_y b_z \vec{u_x} + a_z b_x \vec{u_y} - a_z b_y \vec{u_x} $$

Agrupando finalmente por vectores unitarios:

$$ (a_y b_z - a_z b_y) \vec{u_x} + (a_z b_x - a_x b_z) \vec{u_y} + (a_x b_y - a_y b_x) \vec{u_z} $$

Así queda demostrada la fórmula del producto vectorial en términos de las componentes de los vectores.