Campo vectorial

¿Qué es un campo vectorial?

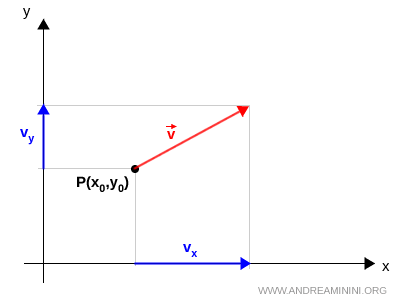
Un campo vectorial es una función F que asigna un vector a cada punto del espacio. $$ \vec{v} = F(x,y,z) $$

Es decir, en cada punto del espacio tridimensional (xyz), se definen tres componentes escalares que determinan la dirección e intensidad del vector en las direcciones de los ejes x, y y z.

En el caso del espacio bidimensional (xy), cada punto queda asociado a dos componentes escalares: las proyecciones del vector sobre los ejes x e y.

¿Los vectores son iguales en todos los puntos o varían?

En un campo vectorial, los vectores pueden variar en dirección, orientación e intensidad a lo largo del espacio, o bien permanecer constantes en toda la región considerada.

Veamos un ejemplo práctico de un campo vectorial definido sobre una región del plano (espacio bidimensional):

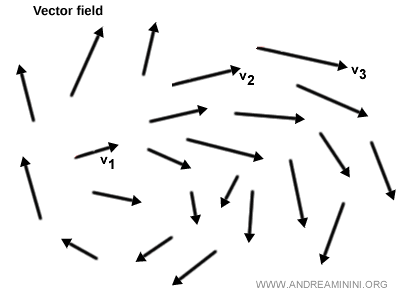
Ejemplo. El viento representado en un mapa meteorológico. En cada punto del mapa, una flecha indica tanto la dirección de procedencia del viento como su intensidad. Este es un ejemplo típico de campo vectorial.

Si todos los vectores son idénticos, se habla de un campo vectorial constante.

Un ejemplo clásico es el campo gravitatorio cerca de la superficie terrestre.

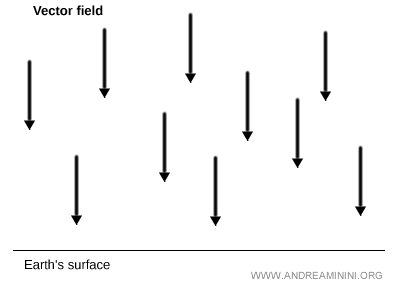
Un campo vectorial también puede definirse en el espacio euclídeo tridimensional.

Por ejemplo, podemos representar la dirección, orientación e intensidad del flujo de aire en torno a una esfera:

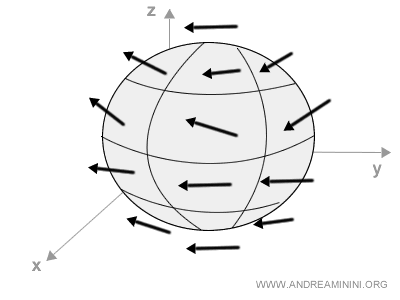
En este caso, cada vector tiene tres componentes que corresponden a sus proyecciones sobre los ejes x, y y z:

$\vec{v}(x, y, z) = \begin{pmatrix} v_x(x,y,z) \\ v_y(x,y,z) \\ v_z(x,y,z) \end{pmatrix}$

De forma más general, un campo vectorial puede depender también del tiempo. En este caso se introduce una cuarta variable, el tiempo: $ F(x, y, z, t) $.

Un ejemplo práctico

Consideremos el siguiente campo vectorial:

$\vec{v}(x,y,z) = (2x,\ -y,\ 3z)$

¿Cuáles son las componentes escalares del vector en el punto $(1,2,3)$?

Las coordenadas del punto en el espacio son:

$$(x_0, y_0, z_0) = (1,2,3)$$

Sustituimos estas coordenadas en la función que define el campo vectorial:

$$ \vec{v}(1,2,3) = (2 \cdot 1,\ -2,\ 3 \cdot 3)$$

$$ \vec{v}(1,2,3) = (2, -2, 9)$$

Las componentes del vector - es decir, los valores escalares que caracterizan el vector en el punto $(1,2,3)$ - son:

$$v_x = 2 $$

$$ v_y = -2 $$

$$ v_z = 9 $$

Por lo tanto:

$\vec{v}(1,2,3) = (2,\ -2,\ 9)$

Esto significa que en el punto $ (1,2,3) $, el vector presenta una componente $ +2 $ en la dirección x, $ -2 $ en la dirección y, y $ +9 $ en la dirección z.

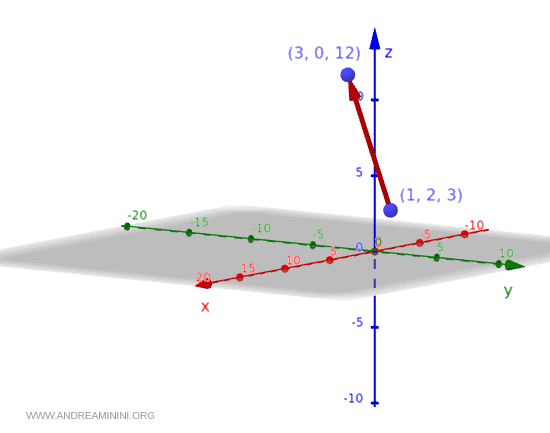
Gráficamente, este vector puede representarse como una flecha que parte del punto $ (1,2,3) $ y apunta hacia el punto $ (3,0,12) $, correspondiente a la suma de las coordenadas del punto y las componentes del vector:

$$ (1,2,3)+(2,-2,9)=(1+2, 2-2, 3+9) = (3,0,12) $$

Así se visualiza en el espacio tridimensional:

Este mismo procedimiento puede aplicarse a todos los puntos del dominio del campo vectorial:

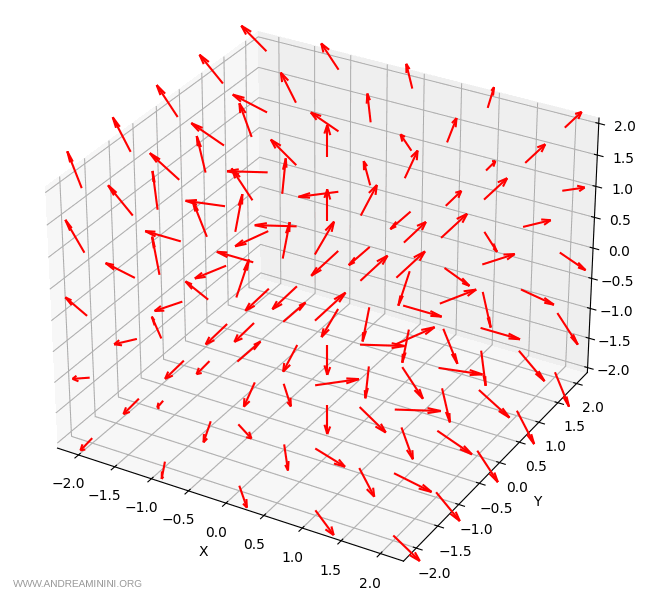
Nota. En la visualización final, los vectores han sido normalizados: es decir, se representan con una misma longitud gráfica para facilitar la lectura. Las direcciones son correctas, pero la longitud dibujada no refleja la magnitud real de cada vector.

La diferencia entre un campo vectorial y un espacio vectorial

Confundir un campo vectorial con un espacio vectorial es un error frecuente entre quienes se inician en este ámbito.

Aunque sus nombres pueden inducir a error, se refieren a conceptos profundamente distintos.

• Espacio vectorial
  Un espacio vectorial (o espacio lineal) es un conjunto de elementos, llamados "vectores", que pueden sumarse entre sí y multiplicarse por escalares (números reales o complejos, por ejemplo), cumpliendo un conjunto específico de axiomas. Estos vectores no se limitan a representaciones geométricas: pueden ser funciones, matrices u otros objetos matemáticos. Se trata de una estructura algebraica abstracta, definida por las operaciones que permite realizar.
• Campo vectorial
  En matemáticas, un campo vectorial es una función que asigna un vector a cada punto de un espacio, generalmente en ℝ² o ℝ³. En física, sin embargo, el término se utiliza con un sentido más amplio, para describir cualquier correspondencia que asocie un vector a cada punto de una región, incluso cuando no exista una fórmula global explícita. Un ejemplo común sería un mapa meteorológico que muestra la dirección e intensidad del viento en distintas zonas geográficas.

Y así sucesivamente.