Momento de un vector
¿Qué es el momento de un vector?
El momento de un vector v, aplicado en un punto P con respecto a un punto O (llamado polo), se define como el producto vectorial entre el vector de posición OP y el propio vector v: $$ \vec{M} = \vec{OP} × \vec{v} $$ La magnitud del momento viene dada por: $$ | \vec{M} | = | \vec{OP} | \cdot | \vec{v} | \cdot \sin θ $$
Aquí, θ es el ángulo comprendido entre los vectores v y OP.
El momento de un vector es, en sí mismo, una magnitud vectorial.
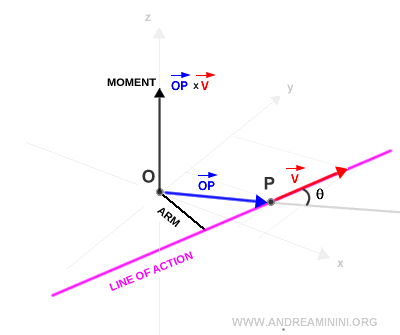
Este vector es perpendicular al plano definido por v y el vector de posición OP, ya que se obtiene a través de un producto vectorial.
Nota. La dirección del vector v se denomina su línea de acción. La distancia más corta entre esta línea de acción y el polo O se conoce como el brazo de momento del vector v con respecto al polo O.
Propiedades del momento de un vector
A continuación se resumen las principales propiedades del momento de un vector:
- La magnitud del momento es nula cuando los vectores v y OP son colineales. Es decir, el momento desaparece si los vectores son paralelos o coinciden. En cambio, es distinto de cero cuando apuntan en direcciones diferentes.
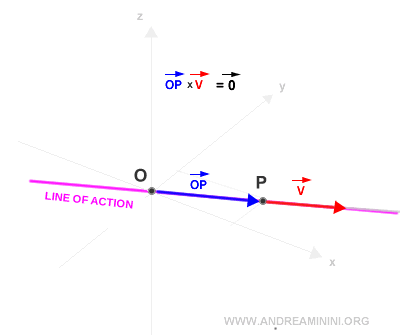
Nota. En este caso, el brazo de momento es cero porque la línea de acción pasa por el polo O. Por lo tanto, el vector momento es nulo.
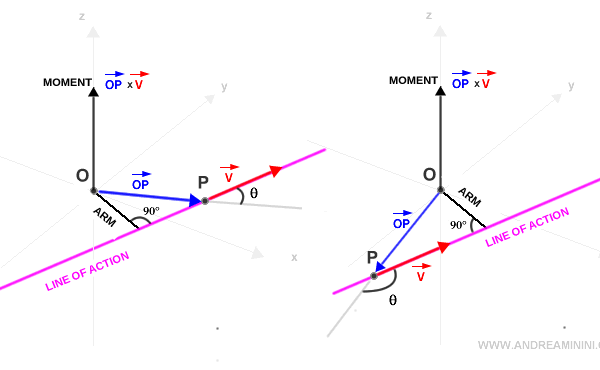
- El desplazamiento del vector v a lo largo de su línea de acción no modifica la magnitud de su momento. Esta propiedad pone de manifiesto la conservación del momento respecto a traslaciones a lo largo de la línea de acción.
Explicación paso a paso
Consideremos un vector aplicado en el punto P y un punto de referencia O, que actuará como polo.
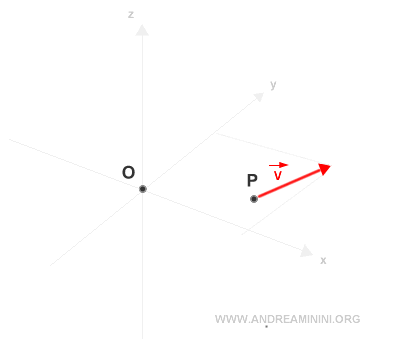
En primer lugar, calculamos el vector de posición de v con respecto a O.
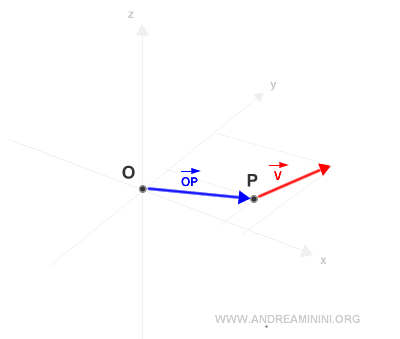
A continuación, trazamos las líneas que representan las direcciones de ambos vectores.
La dirección del vector v define su línea de acción.
Luego, medimos el ángulo θ entre ambos vectores.
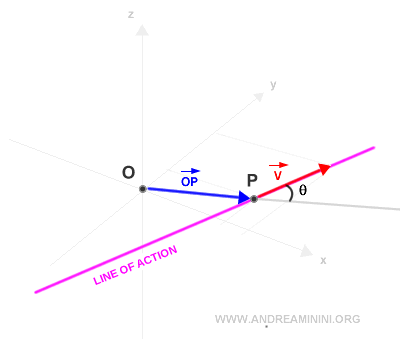
La distancia perpendicular desde la línea de acción hasta el polo se denomina brazo de momento.
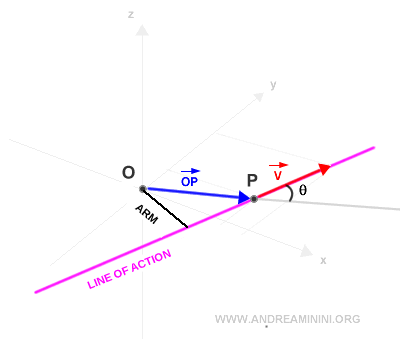
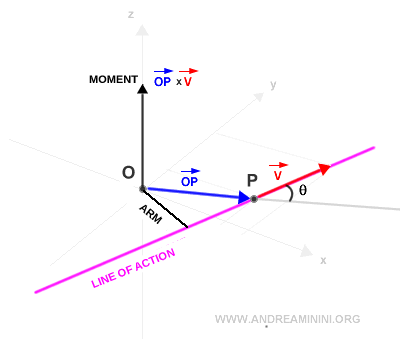
Ahora calculamos el producto vectorial entre el vector de posición OP y el vector v.
El resultado es un vector perpendicular al plano, que corresponde al momento del vector v con respecto al polo O.
Efecto de cambiar el polo
El polo actúa como punto de referencia (o sistema de referencia).

Al cambiar el polo de O a un nuevo punto O' en el plano cartesiano, el momento del vector se modifica.
El nuevo vector momento MO' conserva la misma dirección que el momento original, aunque su magnitud suele variar.
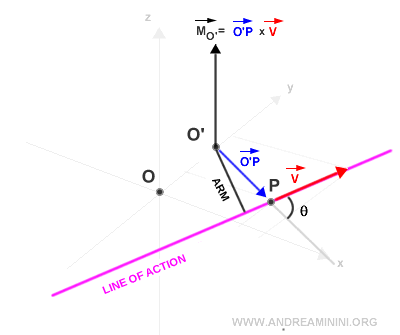
Al cambiar el polo, también varían el ángulo θ, el brazo de momento y la magnitud del momento.
Los dos momentos MO y MO' del vector v están relacionados mediante la siguiente expresión algebraica:
$$ \vec{M_{O'}} = \vec{O'O} × \vec{v} + \vec{M_O} $$
Demostración
El momento del vector v respecto al polo O es:
$$ \vec{M_O} = \vec{OP} × \vec{v} $$
El momento del vector v respecto al polo O' es:
$$ \vec{M_{O'}} = \vec{O'P} × \vec{v} $$
El vector de posición O'P equivale a la suma de los vectores O'O y OP.
Por lo tanto:
$$ \vec{M_{O'}} = ( \vec{O'O} + \vec{OP} ) × \vec{v} $$
Aplicando la propiedad distributiva del producto vectorial:
$$ \vec{M_{O'}} = \vec{O'O} × \vec{v} + \vec{OP} × \vec{v} $$
Dado que MO = OP × v, se obtiene:
$$ \vec{M_{O'}} = \vec{O'O} × \vec{v} + \vec{M_O} $$
Así queda demostrada la relación entre los dos momentos del vector respecto a los polos O y O'.
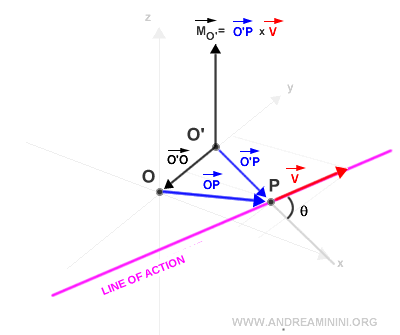
Por tanto, la magnitud del nuevo momento |MO'| tras cambiar el sistema de referencia es:
$$ | \vec{M_{O'}} | = | \vec{O'O} × \vec{v} | + | \vec{M_O} | $$
Nota. Si, al cambiar el polo, el vector O'O es paralelo al vector v, el momento no se ve afectado, ya que el brazo de momento permanece inalterado. $$ \vec{O'O} \ || \ \vec{v} \ \ \Rightarrow \ \ M_{O'}=M_O $$ El siguiente diagrama ilustra este caso particular:
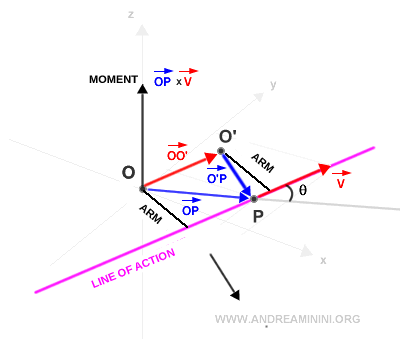
Y así sucesivamente.