Vectores ortogonales
Los vectores ortogonales están relacionados entre sí por la propiedad de ortogonalidad, es decir, son perpendiculares entre sí.
En un espacio vectorial real, dos vectores v1 y v2 son ortogonales si su producto escalar es igual a cero. $$ <v_1,v_2> = 0 $$
El símbolo de una T invertida indica la ortogonalidad entre dos vectores.
$$ v_1 \perp v_2 $$
Nota: Un producto escalar nulo es condición necesaria, pero no suficiente, para la ortogonalidad. Es fundamental además que ninguno de los vectores sea un vector nulo; es decir, ambos deben tener norma distinta de cero. Por ejemplo, el producto escalar de cualquier vector con el vector nulo es cero, pero en ese caso no se consideran ortogonales. $$ < \vec{v} , \vec{0} > = 0 $$
Ejemplo de vectores ortogonales
En el espacio vectorial V=R2 sobre el cuerpo K=R, consideremos dos vectores:
$$ v_1 = ( 1, 0 ) \\ v_2 = ( 0,1 ) $$
El producto escalar euclídeo <v1,v2> de estos dos vectores es igual a cero.
$$ <v_1,v_2> = 1\cdot0 + 0\cdot1 = 0 $$
Por tanto, estos dos vectores son ortogonales.
Nota: Estos vectores v1 y v2 pueden representarse en el plano cartesiano, tomando como referencia el origen O(0,0). La representación gráfica muestra claramente que son geométricamente perpendiculares.
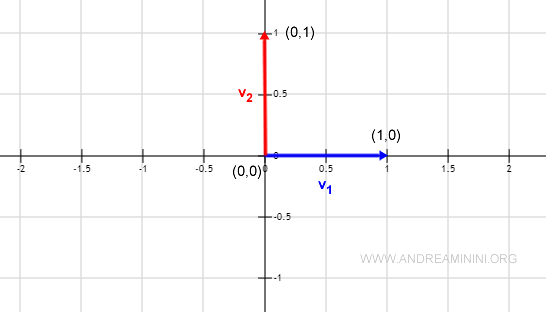
Ejemplo 2
Consideremos ahora otro par de vectores:
$$ v_1 = ( 1, 1 ) \\ v_2 = ( 0,1 ) $$
Su producto escalar no es cero.
$$ <v_1,v_2> = 1\cdot0 + 1\cdot1 = 0+1 = 1 $$
Por tanto, estos vectores no son ortogonales.
Nota: Al representar estos vectores en el plano cartesiano, resulta evidente que no son geométricamente perpendiculares.
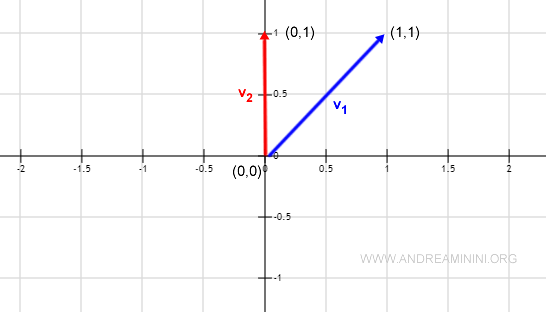
El coseno del ángulo y la ortogonalidad
Cuando ambos vectores son distintos del vector nulo, existe una relación directa entre el coseno del ángulo que forman los vectores v1 y v2, su producto escalar y sus normas.
$$ cos(v_1,v_2) = \frac{ <v_1,v_2> } { ||v_1|| \cdot ||v_2|| }$$
Por convención, si uno de los vectores v1 o v2 es el vector nulo, se define que el coseno es cero:
$$ cos(v_1,v_2) := 0 \:\:si \:\:v_1=0_V \:\:o\:\: v_2=0_V $$
Ejemplo práctico
Calculemos el coseno del ángulo para los siguientes vectores:
$$ v_1 = ( 1, 0 ) \\ v_2 = ( 0,1 ) $$
Su producto escalar es:
$$ <v_1,v_2> = 1\cdot0 + 0\cdot1 = 0 $$
Mientras que las normas de los vectores son:
$$ ||v_1|| = \sqrt{1^2+0^2} = 1 \\ ||v_2|| = \sqrt{0^2+1^2} = 1 $$
Por tanto, el coseno del ángulo entre estos dos vectores es:
$$ cos(v_1,v_2) = \frac{ 0 }{ 1 } = 0 $$
En efecto, el ángulo es de 90° y el coseno es cero.
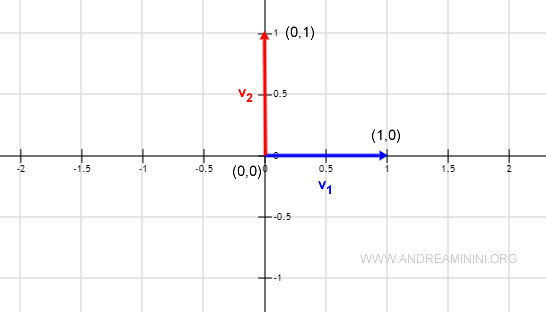
Ejemplo 2
Calculemos ahora el coseno para otro par de vectores:
$$ v_1 = ( 1, 1 ) \\ v_2 = ( 0,1 ) $$
Su producto escalar es:
$$ <v_1,v_2> = 1\cdot0 + 1\cdot1 = 0+1 = 1 $$
Las normas de los vectores son:
$$ ||v_1|| = \sqrt{1^2+1^2} = \sqrt{2} \\ ||v_2|| = \sqrt{0^2+1^2} = 1 $$
Por tanto, el coseno del ángulo entre estos dos vectores es:
$$ cos(v_1,v_2) = \frac { 1 } { \sqrt{2} \cdot 1 } = \frac {1} { \sqrt{2} } $$
Es decir, los vectores forman un ángulo de 45°.
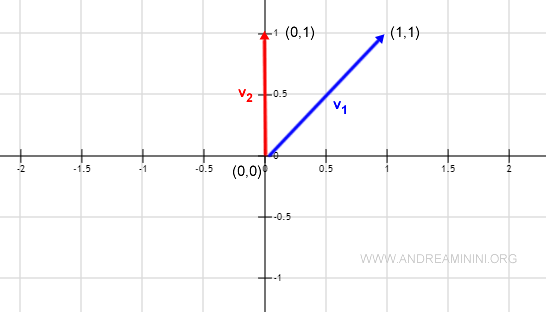
Diferencia entre perpendicularidad y ortogonalidad
Los términos "ortogonalidad" y "perpendicularidad" son sinónimos.
Sin embargo, el término "perpendicularidad" se utiliza con mayor frecuencia en un contexto puramente geométrico, mientras que "ortogonalidad" es un concepto más general que también se aplica en ámbitos no geométricos, como el álgebra lineal y el análisis funcional.
Bases ortogonales y ortonormales
Los vectores ortogonales permiten construir tanto bases ortogonales como bases ortonormales.
- Una base ortogonal está formada por vectores ortogonales entre sí.
- Una base ortonormal es una base ortogonal cuyos vectores, además, tienen norma unitaria.