Base ortonormal
Una base ortonormal de un espacio vectorial B{v,w} es un conjunto de vectores ortogonales $$ <v,w>=0 \:\:si\:\: v \ne w $$ cuyos elementos tienen norma unitaria: $$ || \vec{v} || = || \vec{w} || = 1 $$
En otras palabras, una base ortonormal debe cumplir dos condiciones fundamentales:
- Los vectores de la base tienen norma unitaria; es decir, su magnitud (longitud) es exactamente 1.
- Los vectores son distintos y ortogonales entre sí; en consecuencia, su producto escalar <v,w> es cero.
Nota. Los vectores de una base ortonormal también se denominan vectores de norma unitaria, ya que la norma de cada vector es igual a 1: $$ ||v|| = 1 $$ $$ ||w|| = 1 $$ Esta propiedad se deduce del hecho de que el producto escalar <v,w> = 1 cuando v = w. La norma inducida por el producto escalar se define como: $$ ||v|| = \sqrt{ <v,v> } $$ Por tanto, si v = w, es necesario que <v,w> = 1 para que la norma sea unitaria.
Ejemplo de una base ortonormal
El siguiente conjunto constituye un ejemplo práctico de base ortonormal.
Se trata de la base canónica del plano.
$$ B = \{ \vec{v_1} \ , \ \vec{v_2} \} = \{ \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \end{pmatrix} \} $$
Ambos vectores tienen norma unitaria:
$$ ||\vec{v}|| = \sqrt{1^2+0^2} = 1 $$
$$ ||\vec{w}|| = \sqrt{0^2+1^2} = 1 $$
Además, los dos vectores son distintos y su producto escalar es cero:
$$ <v,w>= ( 1 \cdot 0 ) + ( 0 \cdot 1 ) = 0+0 = 0 $$
Por tanto, forman una base ortonormal.
Gráficamente, los dos vectores forman un ángulo de 90° (son ortogonales) y tienen longitud (magnitud) igual a 1.
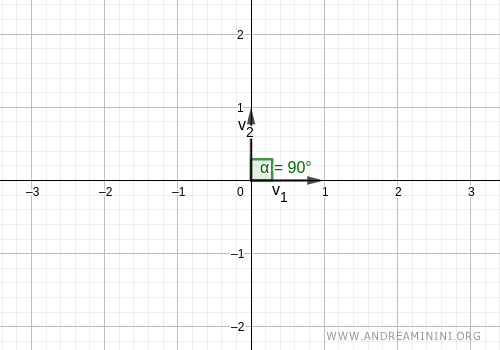
Nota. En una base ortonormal, los vectores son vectores de norma unitaria. Esta es otra manera de verificar la ortonormalidad de la base: $$ ||v|| = \sqrt{1^2+0^2}=1 $$ $$ ||w|| = \sqrt{0^2+1^2}=1 $$
Diferencia entre bases ortogonales y bases ortonormales
Una base ortonormal es siempre una base ortogonal, ya que sus vectores son ortogonales entre sí.
Sin embargo, la recíproca no es necesariamente cierta: una base ortogonal no siempre es ortonormal.
Ejemplo
El siguiente conjunto constituye una base ortogonal:
$$ B = \{ \begin{pmatrix} 1 \\ -1 \end{pmatrix} , \begin{pmatrix} 1 \\ 1 \end{pmatrix} \} $$
Se trata de dos vectores distintos cuyo producto escalar es cero:
$$ <v,w>= ( 1 \cdot 1 ) + ( -1 \cdot 1 ) = 1-1 = 0 $$
Por tanto, los dos vectores forman un ángulo de 90°; es decir, son vectores ortogonales.
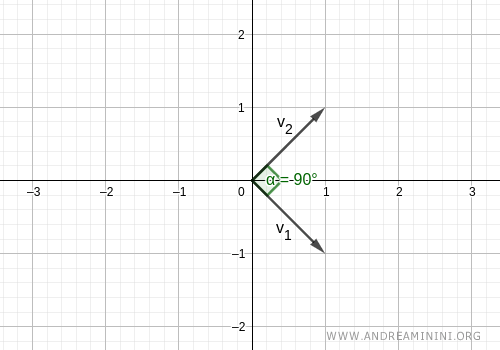
No obstante, esta no es una base ortonormal, ya que los vectores no tienen norma unitaria:
$$ ||v_1|| = \sqrt{1^2+(-1)^2}=\sqrt{2} $$ $$ ||v_2|| = \sqrt{1^2+1^2}=\sqrt{2} $$
Gráficamente, esto significa que la longitud (magnitud) de los vectores es distinta de 1.
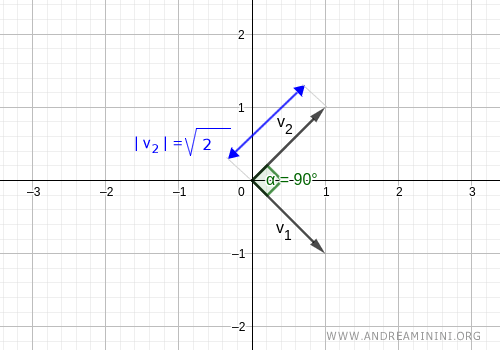
Aunque los vectores son ortogonales, no forman una base ortonormal.
Nota. Cualquier base ortogonal puede transformarse en una base ortonormal normalizando los vectores que la componen. Para más información, consulta cómo transformar una base ortogonal en una base ortonormal.