Producto escalar de dos vectores

El producto escalar (o producto interno) entre dos vectores es una operación que da como resultado un número real (escalar). Se calcula multiplicando la magnitud de un vector por la magnitud de la proyección del segundo vector sobre el primero: $$ \vec{x} \cdot \vec{y} = | \vec{x} | \cdot | \vec{y} | \cdot \cos \theta $$ donde θ es el ángulo entre los dos vectores. De forma equivalente, el producto escalar puede obtenerse sumando los productos de los componentes correspondientes: \[ \vec{x} \cdot \vec{y} = x_1 y_1 + x_2 y_2 + \ldots + x_n y_n \]

También se conoce como producto interno, y suele representarse con las notaciones <v₁, v₂>, (v₁, v₂) o v₁•v₂.

Es importante señalar que el producto escalar de dos vectores, como <v₁, v₂>, es un número real. Esto lo distingue claramente del producto de un vector por un escalar k, que genera un nuevo vector.

¿Por qué es importante?

El producto escalar posee propiedades geométricas de gran utilidad:

• Si dos vectores son ortogonales (perpendiculares), su producto escalar es cero.
  

  
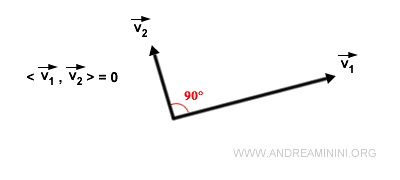
  Esto ocurre porque el coseno de un ángulo de 90° es cero. Por tanto, un producto escalar nulo sugiere que los vectores son ortogonales.

  Sin embargo, un producto escalar igual a cero también puede deberse a que uno o ambos vectores son el vector nulo. Algunas observaciones relevantes:
  
  
  • El producto escalar de un vector consigo mismo es cero únicamente si se trata del vector nulo: $$ \langle \vec{v}, \vec{v} \rangle = 0 \ \Leftrightarrow \ \vec{v} = \{ \oslash \} $$
  • Para un vector no nulo, el producto escalar consigo mismo es el cuadrado de su magnitud: $$ \langle \vec{v}, \vec{v} \rangle = |\vec{v}|^2 \ \Leftrightarrow \ \vec{v} \ne \{ \oslash \} $$
• Si dos vectores son paralelos o coinciden, su producto escalar equivale al producto de sus magnitudes. Esto se debe a que el coseno de un ángulo de 0° es uno, de modo que <v₁, v₂> = |v₁| · |v₂|.
  
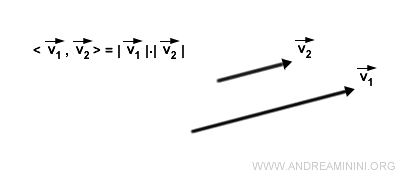
• El producto escalar permite calcular la magnitud de un vector y el ángulo entre dos vectores.

Propiedades del producto escalar. A continuación, se resumen sus principales propiedades:

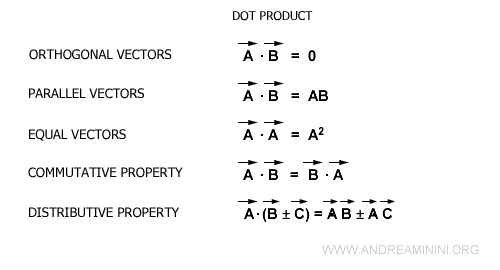
Conviene recordar que el producto escalar con el vector nulo siempre es cero, ya que su magnitud es nula. Por ello, un producto escalar nulo sugiere que los vectores podrían ser ortogonales, aunque no lo garantiza.

Ejemplo práctico con vectores

Consideremos dos vectores en el espacio bidimensional \( \mathbb{R}^2 \):

$$ \vec{v_1} = \begin{pmatrix} 4 \\ 1 \end{pmatrix} $$

$$ \vec{v_2} = \begin{pmatrix} 2 \\ 2 \end{pmatrix} $$

Representación gráfica:

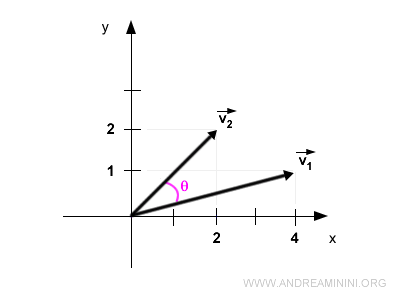
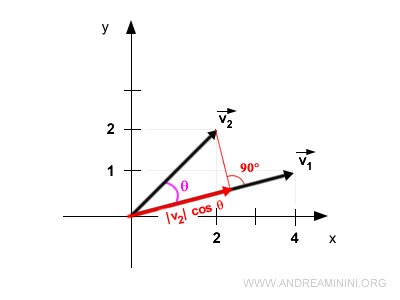
Estos vectores forman un ángulo θ = 30,96°.

Para calcular su producto escalar:

$$ \langle \vec{v_1}, \vec{v_2} \rangle = \vec{v_1} \cdot \vec{v_2} $$

Proyectando ortogonalmente el vector v₂ sobre v₁, se obtiene un nuevo vector cuya magnitud es |v₂| · cos θ, dirigido en la misma dirección que v₁.

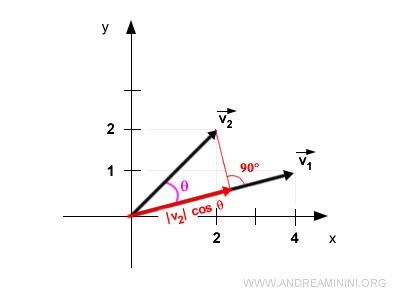
El producto de las magnitudes de estos vectores es:

$$ \langle \vec{v_1}, \vec{v_2} \rangle = |\vec{v_1}| \cdot \left( |\vec{v_2}| \cdot \cos \theta \right) $$

Con |v₁| = 4,12 y |v₂| = 2,83:

$$ \langle \vec{v_1}, \vec{v_2} \rangle = 4,12 \cdot \left( 2,83 \cdot \cos \theta \right) $$

$$ \langle \vec{v_1}, \vec{v_2} \rangle = 4,12 \cdot \left( 2,83 \cdot \cos 30,96^\circ \right) $$

Como cos 30,96° = 0,86:

$$ \langle \vec{v_1}, \vec{v_2} \rangle = 4,12 \cdot \left( 2,83 \cdot 0,86 \right) $$

$$ \langle \vec{v_1}, \vec{v_2} \rangle = 4,12 \cdot 2,43 $$

Nota. El término 2,83 · cos(30,96°) corresponde a la magnitud de la proyección de v₂ sobre v₁, es decir, |v₂| · cos θ.

Por tanto, el producto escalar es:

$$ \langle \vec{v_1}, \vec{v_2} \rangle = 4,12 \cdot 2,43 $$

$$ \langle \vec{v_1}, \vec{v_2} \rangle = 10 $$

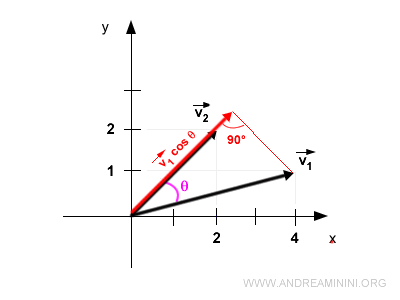
Nota. El producto escalar es conmutativo. Por lo tanto, proyectar v₁ sobre v₂ produce el mismo resultado.

Cálculo directo

Una forma directa de calcular el producto escalar es mediante la fórmula euclídea:

$$ \langle \vec{v_1}, \vec{v_2} \rangle = v_{1x} \cdot v_{2x} + v_{1y} \cdot v_{2y} + v_{1z} \cdot v_{2z} $$

Este método es rápido y sencillo: basta con multiplicar los componentes correspondientes y sumar los resultados.

 

 

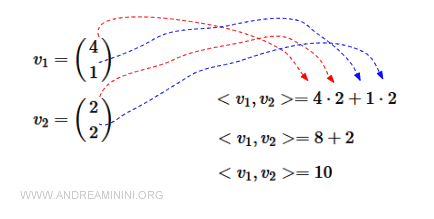
En nuestro caso, los componentes en x son 4 y 2, y los componentes en y son 1 y 2.

Este resultado coincide con el obtenido previamente.

Propiedades del producto escalar

El producto escalar de dos vectores pertenecientes al mismo espacio vectorial V sobre el cuerpo K=ℝ es una función simétrica y bilineal. En otras palabras, para los vectores v₁ y v₂ se tiene:

$$ \langle \cdot, \cdot \rangle \:\: := \:\: V \times V \:\: \rightarrow \:\: \mathbb{R} $$

Producto escalar euclídeo

Entre las diferentes definiciones de producto escalar, el producto escalar euclídeo se define como: $$ \langle v_1 , v_2 \rangle = v_{1x} \cdot v_{2x} + v_{1y} \cdot v_{2y} + v_{1z} \cdot v_{2z} $$

Ejemplo

Consideremos dos vectores $v_1$ y $v_2$ en $V = \mathbb{R}^3$:

$$ v_1 = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}, \quad v_2 = \begin{pmatrix} 3 \\ -1 \\ 0 \end{pmatrix} $$

Su producto escalar euclídeo es:

$$ \langle v_1 , v_2 \rangle = (2 \cdot 3) + ((-1) \cdot (-1)) + (1 \cdot 0) $$

$$ \langle v_1 , v_2 \rangle = 6 + 1 + 0 = 7 $$

Nota. El producto escalar es no degenerado: si $\langle w, v \rangle = 0$ para todo vector $w$ en $V$, entonces $v$ es necesariamente el vector nulo.

Demostración de la fórmula del producto escalar

Sean dos vectores $\vec{a}$ y $\vec{b}$. Su producto escalar es:

$$ \vec{a} \cdot \vec{b} $$

donde:

$$ \vec{a} = a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z} $$

$$ \vec{b} = b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} $$

Expandimos esta expresión aplicando la propiedad distributiva, teniendo en cuenta que el producto escalar entre vectores unitarios ortogonales es nulo:

$$ \vec{a} \cdot \vec{b} = ( a_x \vec{u_x} + a_y \vec{u_y} + a_z \vec{u_z} ) \cdot ( b_x \vec{u_x} + b_y \vec{u_y} + b_z \vec{u_z} ) $$

$$ = a_x \vec{u_x} b_x \vec{u_x} + a_x \vec{u_x} b_y \vec{u_y} + a_x \vec{u_x} b_z \vec{u_z} + $$

$$ + a_y \vec{u_y} b_x \vec{u_x} + a_y \vec{u_y} b_y \vec{u_y} + a_y \vec{u_y} b_z \vec{u_z} + $$

$$ + a_z \vec{u_z} b_x \vec{u_x} + a_z \vec{u_z} b_y \vec{u_y} + a_z \vec{u_z} b_z \vec{u_z} $$

Como el producto escalar entre dos vectores ortogonales es cero, se anulan los términos cruzados:

$$ \vec{u_x} \cdot \vec{u_y} = \vec{u_y} \cdot \vec{u_x} = 0 $$ $$ \vec{u_x} \cdot \vec{u_z} = \vec{u_z} \cdot \vec{u_x} = 0 $$ $$ \vec{u_y} \cdot \vec{u_z} = \vec{u_z} \cdot \vec{u_y} = 0 $$

Por lo tanto, la expresión se reduce a tres términos:

$$ a_x \vec{u_x} b_x \vec{u_x} + a_y \vec{u_y} b_y \vec{u_y} + a_z \vec{u_z} b_z \vec{u_z} $$

Podemos escribirlo como:

$$ a_x b_x ( \vec{u_x} \cdot \vec{u_x} ) + a_y b_y ( \vec{u_y} \cdot \vec{u_y} ) + a_z b_z ( \vec{u_z} \cdot \vec{u_z} ) $$

El producto escalar de un vector consigo mismo equivale al cuadrado de su magnitud, ya que $\cos 0^\circ = 1$:

Nota. $$ \vec{v} \cdot \vec{v} = | \vec{v} |^2 $$

Dado que los vectores unitarios tienen magnitud uno, se verifica que:

$$ \vec{u_x} \cdot \vec{u_x} = 1, \quad \vec{u_y} \cdot \vec{u_y} = 1, \quad \vec{u_z} \cdot \vec{u_z} = 1 $$

Así, la expresión final queda:

$$ a_x b_x (1) + a_y b_y (1) + a_z b_z (1) $$

$$ = a_x b_x + a_y b_y + a_z b_z $$

En conclusión, hemos demostrado que el producto escalar de dos vectores es igual a la suma de los productos de sus componentes en las direcciones $x$, $y$ y $z$:

$$ \vec{a} \cdot \vec{b} = a_x b_x + a_y b_y + a_z b_z $$

Norma inducida por el producto escalar

Existe una relación directa entre el producto escalar de un vector y su norma (o magnitud).

La norma de un vector se define como la raíz cuadrada de su producto escalar consigo mismo:

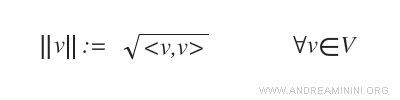
Esta norma recibe el nombre de norma inducida por el producto escalar.

Nota. La norma representa la longitud del vector, y también se denomina su magnitud.

Ejemplo

Consideremos un vector $v_1$ en el espacio vectorial $V = \mathbb{R}^3$ sobre el cuerpo $K = \mathbb{R}$:

$$ v_1 = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix} $$

La norma del vector es:

$$ || v_1 || = \sqrt{ \langle v_1, v_1 \rangle } $$

$$ || v_1 || = \sqrt{ (2 \cdot 2) + ((-1) \cdot (-1)) + (1 \cdot 1) } $$

$$ || v_1 || = \sqrt{ 4 + 1 + 1 } $$

$$ || v_1 || = \sqrt{6} $$

Desigualdad de Cauchy-Schwarz

La desigualdad de Cauchy-Schwarz establece que:

El valor absoluto del producto escalar de dos vectores $\langle v_1, v_2 \rangle$ es menor o igual que el producto de sus normas $||v_1|| \cdot ||v_2||$, inducidas por el producto escalar.

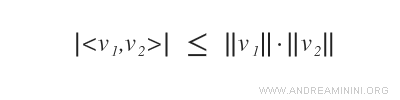
Si el producto escalar es igual al producto de las normas, los vectores son linealmente dependientes.

 

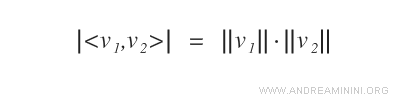
Ejemplo

Consideremos dos vectores $v_1$ y $v_2$ en el espacio vectorial $V = \mathbb{R}^3$:

$$ v_1 = \begin{pmatrix} 2 \\ -1 \\ 1 \end{pmatrix}, \quad v_2 = \begin{pmatrix} 3 \\ -1 \\ 0 \end{pmatrix} $$

El valor absoluto del producto escalar es:

$$ |\langle v_1, v_2 \rangle| = |7| = 7 $$

Las normas de ambos vectores son:

$$ || v_1 || = \sqrt{ (2 \cdot 2) + ((-1) \cdot (-1)) + (1 \cdot 1) } = \sqrt{6} $$

$$ || v_2 || = \sqrt{ (3 \cdot 3) + ((-1) \cdot (-1)) + (0 \cdot 0) } = \sqrt{10} $$

Aplicando la desigualdad de Cauchy-Schwarz:

$$ |\langle v_1, v_2 \rangle| \le || v_1 || \cdot || v_2 || $$

$$ 7 \le \sqrt{6} \cdot \sqrt{10} $$

$$ 7 \le 7.7459 $$

Por lo tanto, según la desigualdad, los vectores no son linealmente dependientes.

Ejemplo 2

Consideremos ahora dos vectores linealmente dependientes:

$$ v_1 = \begin{pmatrix} -1 \\ 1 \end{pmatrix}, \quad v_2 = \begin{pmatrix} 1 \\ -1 \end{pmatrix} $$

Nota. El determinante de la matriz formada por estos dos vectores es cero, lo que confirma su dependencia lineal.

El valor absoluto del producto escalar es:

$$ |\langle v_1, v_2 \rangle| = |(-1 \cdot 1) + (1 \cdot -1)| = 2 $$

Las normas de ambos vectores son:

$$ || v_1 || = \sqrt{ (-1 \cdot -1) + (1 \cdot 1) } = \sqrt{2} $$

$$ || v_2 || = \sqrt{ (1 \cdot 1) + (-1 \cdot -1) } = \sqrt{2} $$

Aplicando la desigualdad:

$$ |\langle v_1, v_2 \rangle| \le || v_1 || \cdot || v_2 || $$

$$ 2 \le \sqrt{2} \cdot \sqrt{2} $$

$$ 2 = 2 $$

En este caso, se verifica la igualdad, lo que confirma que los vectores son linealmente dependientes.

Notas

Observaciones relevantes sobre el producto escalar:

• A diferencia del producto de números reales, el producto escalar puede ser cero aun cuando ninguno de los vectores sea nulo (por ejemplo, si son perpendiculares).
• Si los vectores tienen la misma dirección y el mismo sentido, el producto escalar es el producto de sus magnitudes.
• Si tienen la misma dirección pero sentido opuesto, el producto escalar es el opuesto del producto de sus magnitudes.