Relación entre el producto escalar y la longitud de un vector
El producto escalar de un vector consigo mismo es igual al cuadrado de su magnitud: $$ \vec{v} \cdot \vec{v} = | \vec{v} |^2 $$
Esta propiedad resulta especialmente útil, ya que nos permite calcular la longitud (magnitud o norma) de un vector de manera sencilla.
Para ello, basta con tomar la raíz cuadrada del producto escalar del vector consigo mismo:
$$ | \vec{v} | = \sqrt{ \vec{v} \cdot \vec{v} } $$
Un ejemplo práctico
Consideremos el siguiente vector:
$$ \vec{v} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} $$
Su representación gráfica es la siguiente:
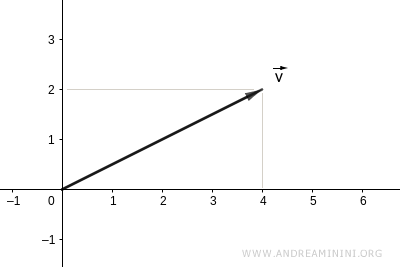
Para calcular su magnitud (o norma), comenzamos evaluando el producto escalar del vector consigo mismo:
$$ \vec{v} \cdot \vec{v} = 2 \cdot 2 + 4 \cdot 4 = 2^2 + 4^2 = 4
+ 16 = 20 $$
Como el producto escalar del vector consigo mismo equivale al cuadrado de su magnitud:
$$ | \vec{v} |^2 = \vec{v} \cdot \vec{v} = 20 $$
Obtenemos entonces la magnitud tomando la raíz cuadrada del resultado:
$$ | \vec{v} | = \sqrt{ 20 } $$
De este modo, determinamos la longitud del vector:
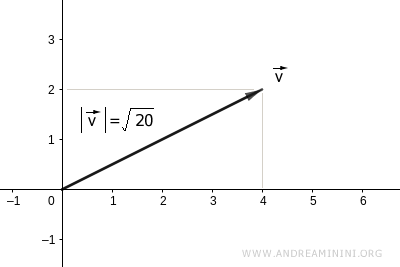
Demostración
Consideremos un vector con coordenadas (x, y):
$$ \vec{v} = \begin{pmatrix} x \\ y \end{pmatrix} $$
Para simplificar, trabajaremos con un vector en dos dimensiones, aunque este razonamiento se aplica igualmente a vectores en espacios de cualquier dimensión.
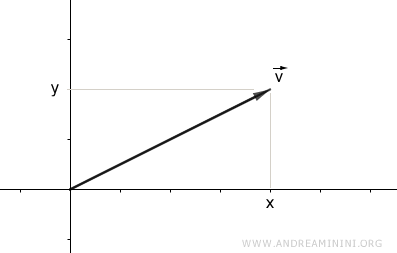
La proyección de las coordenadas del vector (x, y) sobre los ejes cartesianos forma un triángulo rectángulo ABC.
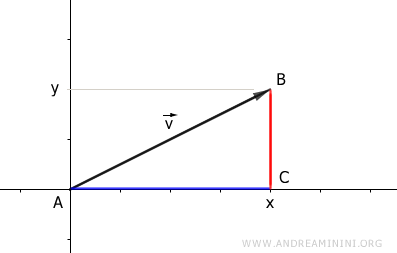
En dicho triángulo, las proyecciones sobre los ejes corresponden a los catetos, mientras que la longitud del vector (su magnitud) se corresponde con la hipotenusa.
El producto escalar del vector consigo mismo es igual a la suma de los cuadrados de los catetos del triángulo:
$$ \vec{v} \cdot \vec{v} = x \cdot x + y \cdot y = x^2 + y^2 $$
De acuerdo con el Teorema de Pitágoras, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa:
$$ \overline{AB}^2 = \overline{BC}^2 + \overline{AC}^2 $$
En este contexto, AC = x, BC = y, y AB representa la longitud (magnitud) del vector |v|:
$$ | \vec{v} |^2 = x^2 + y^2 $$
Por lo tanto, el producto escalar de un vector consigo mismo nos proporciona el cuadrado de su magnitud:
$$ \vec{v} \cdot \vec{v} = x^2 + y^2 = | \vec{v} |^2 $$
De aquí se deduce que la magnitud del vector es la raíz cuadrada de dicho producto:
$$ | \vec{v} | = \sqrt{\vec{v} \cdot \vec{v}} $$
Nota: La magnitud de un vector también se conoce como su norma. Los términos "magnitud" y "norma" hacen referencia al mismo valor escalar, que corresponde a la longitud del vector: $$ || \vec{v} || = \sqrt{\vec{v} \cdot \vec{v}} $$
Y así sucesivamente.