Ángulo entre dos vectores
Para determinar el ángulo entre dos vectores, utilizo una fórmula basada en el arco coseno. Esta se fundamenta en el cociente entre el producto escalar de los vectores y el producto de sus módulos. $$ \alpha = \arccos \left( \frac{\vec{v} \cdot \vec{w}}{ |\vec{v}| \cdot |\vec{w}|} \right) $$
Esta fórmula es válida independientemente del cuadrante en el que se encuentren los vectores.
Siempre devuelve el ángulo más pequeño entre ambos vectores, comprendido entre 0° y 180°, sin importar su orientación en el plano.
Ejemplo
Veamos un ejemplo práctico para ilustrarlo:
Se tienen los siguientes dos vectores:
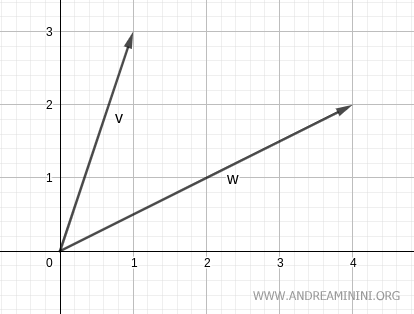
$$ \vec{v} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} $$
$$ \vec{w} = \begin{pmatrix} 4 \\ 2 \end{pmatrix} $$
Al representarlos gráficamente, ambos se encuentran en el plano.
Para calcular el ángulo entre ellos, aplico la fórmula:
$$ \alpha = \arccos \left( \frac{\vec{v} \cdot \vec{w}}{ |\vec{v}| \cdot |\vec{w}|} \right) $$
En primer lugar, calculo el producto escalar:
$$ \vec{v} \cdot \vec{w} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} \cdot \begin{pmatrix} 4 \\ 2 \end{pmatrix} = 1 \cdot 4 + 3 \cdot 2 = 4 + 6 = 10 $$
Ahora sustituyo este valor en la fórmula:
$$ \alpha = \arccos \left( \frac{10}{ |\vec{v}| \cdot |\vec{w}|} \right) $$
A continuación, calculo los módulos de los vectores aplicando el teorema de Pitágoras:
$$ |\vec{v}| = \sqrt{3^2 + 1^2} = \sqrt{10} $$
$$ |\vec{w}| = \sqrt{4^2 + 2^2} = \sqrt{20} $$
Con estos valores obtenidos, procedo a completar la fórmula:
$$ \alpha = \arccos \left( \frac{10}{ \sqrt{10} \cdot \sqrt{20} } \right) $$
$$ \alpha = \arccos \left( \frac{10}{ \sqrt{200} } \right) $$
$$ \alpha = \arccos ( 0,71 ) $$
De donde se obtiene:
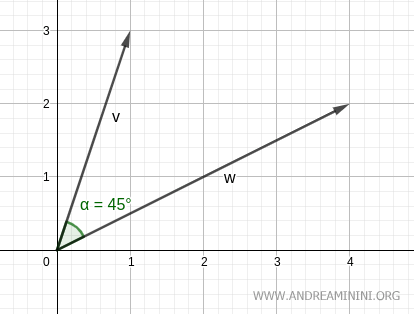
$$ \alpha = 45^\circ $$
Por lo tanto, el ángulo entre estos dos vectores es de 45°.
Ejemplo 2
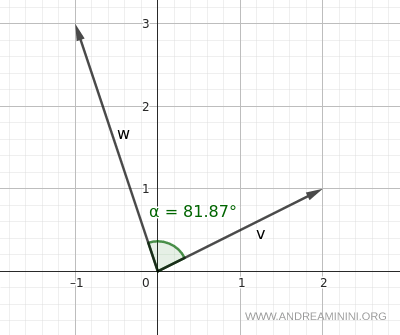
Ahora consideremos dos vectores situados en cuadrantes diferentes:
$$ \vec{v} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} \quad \text{(primer cuadrante)} $$
$$ \vec{w} = \begin{pmatrix} -1 \\ 3 \end{pmatrix} \quad \text{(segundo cuadrante)} $$
El producto escalar de estos vectores es:
$$ \vec{v} \cdot \vec{w} = 2 \cdot (-1) + 1 \cdot 3 = -2 + 3 = 1 $$
Los módulos son:
$$ |\vec{v}| = \sqrt{2^2 + 1^2} = \sqrt{5} $$
$$ |\vec{w}| = \sqrt{(-1)^2 + 3^2} = \sqrt{10} $$
Por tanto, el ángulo entre los vectores es:
$$ \alpha = \arccos \left( \frac{1}{\sqrt{5} \cdot \sqrt{10}} \right) = \arccos \left( \frac{1}{\sqrt{50}} \right) \approx \arccos(0.141) \approx 81.87^\circ $$
El ángulo resultante es aproximadamente 81.87°:
$$ \alpha \approx 81.87^\circ $$
Aunque los vectores se encuentran en cuadrantes distintos - lo que afecta al signo de sus componentes - la fórmula sigue proporcionando correctamente el ángulo (no orientado) entre ellos, que siempre se encuentra en el intervalo de 0° a 180°. Al no tratarse de un ángulo orientado, nunca será de 270°.
Demostración
Para quienes deseen conocer la demostración.
El producto escalar de dos vectores es igual al producto de sus módulos por el coseno del ángulo que los separa:
$$ \vec{v} \cdot \vec{w} = |\vec{v}| \cdot |\vec{w}| \cdot \cos \alpha $$
A partir de esta relación, puedo despejar el coseno del ángulo α:
$$ \cos \alpha = \frac{ \vec{v} \cdot \vec{w} }{|\vec{v}| \cdot |\vec{w}|} $$
Aplicando el arco coseno a ambos lados de la ecuación:
$$ \arccos( \cos \alpha ) = \arccos \left( \frac{ \vec{v} \cdot \vec{w} }{|\vec{v}| \cdot |\vec{w}| } \right) $$
Como el arco coseno es la función inversa del coseno, el resultado de esta operación nos da directamente el valor del ángulo α:
$$ \alpha = \arccos \left( \frac{ \vec{v} \cdot \vec{w} }{|\vec{v}| \cdot |\vec{w}| } \right) $$
De este modo se confirma la validez de la fórmula utilizada para calcular el ángulo entre dos vectores.