Complemento ortogonal
El complemento ortogonal (o suplemento ortogonal) es un subespacio W* del espacio vectorial V que contiene todos los vectores que son ortogonales a cada vector w de un subespacio vectorial W.
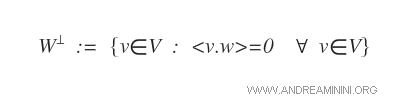
El complemento ortogonal se denota mediante el símbolo de T invertida.
En un espacio vectorial V de dimensión finita, los subespacios W y W* son subespacios suplementarios.
Es decir, la suma directa de W y W* es igual a todo el espacio vectorial V.
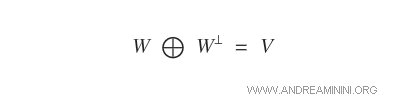
Cálculo de los vectores del complemento ortogonal
Un vector v ∈ V pertenece al complemento ortogonal W* si, y solo si, es ortogonal a todos los elementos de la base BW = { w₁, …, wₙ } del subespacio W.
Esto equivale a resolver un sistema de ecuaciones cartesianas:
$$ \begin{cases} <v,w_1> = c_{11} v_1 + … + c_{1n} v_n = 0 \\ <v,w_2> = c_{21} v_1 + … + c_{2n} v_n = 0 \\ ⋮ \\ <v,w_k> = c_{k1} v_1 + … + c_{kn} v_n = 0 \end{cases} $$
Donde los coeficientes c representan las componentes de cada vector w de la base de W:
$$ W = B \{ w_1, w_2, …, w_k \} $$
El vector v es un vector genérico del espacio V, que puede o no pertenecer al complemento ortogonal.
Nota. Este sistema es homogéneo, ya que para que un vector v sea ortogonal a un vector w, el producto escalar <v,w> debe ser igual a 0.
Ejemplo de cálculo
En el espacio vectorial V = R4 sobre el cuerpo K = R, consideremos el subespacio W generado por la siguiente base:
$$ B_W = \{ w_1, w_2 \} \\ w_1 = (1,1,1,1) \\ w_2 = (1,0,1,0) $$
Queremos determinar los vectores v ∈ V que sean ortogonales a los vectores de la base B.
$$ v = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix} $$
Como la base consta de dos vectores, debemos resolver el siguiente sistema:
$$ \begin{cases} x_1 + x_2 + x_3 + x_4 = 0 \\ x_1 + x_3 = 0 \end{cases} $$
Reescribiendo el sistema:
$$ \begin{cases} -x_3 + x_2 + x_3 + x_4 = 0 \\ x_1 = -x_3 \end{cases} $$
Lo que conduce a:
$$ \begin{cases} x_2 = -x_4 \\ x_1 = -x_3 \end{cases} $$
Por tanto, los vectores que generan la base del complemento ortogonal W* son:
$$ v = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{pmatrix} = B_{W*} \left\{ \begin{pmatrix} 0 \\ 1 \\ 0 \\ -1 \end{pmatrix}, \begin{pmatrix} 1 \\ 0 \\ -1 \\ 0 \end{pmatrix} \right\} $$
Todos los vectores generados a partir de esta base pertenecen al complemento ortogonal.
Ejemplo. El vector v = (3,2,-3,-2) pertenece al complemento ortogonal, ya que se puede expresar como combinación lineal de los vectores de la base de W*: $$ v = \begin{pmatrix} 3 \\ 2 \\ -3 \\ -2 \end{pmatrix} = 2 \begin{pmatrix} 0 \\ 1 \\ 0 \\ -1 \end{pmatrix} + 3 \begin{pmatrix} 1 \\ 0 \\ -1 \\ 0 \end{pmatrix} $$