Bases ortogonales
En un espacio vectorial B{v,w}, una base ortogonal está formada por vectores ortogonales. Es decir, el producto escalar de cualquier par de vectores es igual a cero. $$ <v,w>=0 \:\:\:\: \forall \ v,w $$
Esta condición de ortogonalidad debe cumplirse para cada par de vectores del conjunto.
Ejemplo de una base ortogonal
El siguiente conjunto constituye un ejemplo práctico de base ortogonal, compuesta por vectores ortogonales.
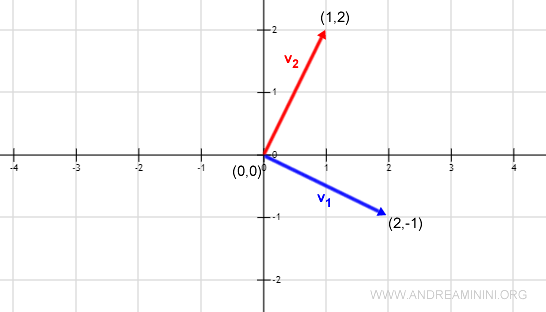
$$ B = \{ \begin{pmatrix} 2 \\ -1 \end{pmatrix} , \begin{pmatrix} 1 \\ 2 \end{pmatrix} \} $$
$$ <v_1,v_2> = 2\cdot(1) + (-1)\cdot2 = 2 - 2 = 0 $$
Nota. La representación gráfica de estos vectores en el plano permite visualizar claramente su perpendicularidad.
Diferencia entre bases ortogonales y bases ortonormales
Una base ortogonal se convierte en una base ortonormal cuando sus vectores, además de ser ortogonales, tienen norma unitaria; es decir, el producto escalar es igual a 1 cuando se toma el mismo vector, y a 0 cuando se trata de vectores distintos.
Ejemplo
El siguiente conjunto es a la vez una base ortogonal y ortonormal:
$$ B = \{ \begin{pmatrix} 1 \\ 0 \end{pmatrix} , \begin{pmatrix} 0 \\ 1 \end{pmatrix} \} $$
El producto escalar entre vectores distintos es cero:
$$ <v,w>= ( 1 \cdot 0 ) + ( 0 \cdot 1 ) = 0+0 = 0 $$
El producto escalar de un vector consigo mismo es igual a 1:
$$ <v,v>= ( 1 \cdot 1 ) + ( 0 \cdot 0 ) = 1+0 = 1 $$
$$ <w,w>= ( 0 \cdot 0 ) + ( 1 \cdot 1 ) = 0+1 = 1 $$
Transformación de una base ortogonal en una base ortonormal
Cualquier base ortogonal puede transformarse en una base ortonormal normalizando sus vectores, es decir, dividiendo cada uno de ellos por su propia norma.
Nota. Para más información, consulta cómo transformar una base ortogonal en una base ortonormal.