Espacios vectoriales

¿Qué es un espacio vectorial?

Un espacio vectorial sobre un campo K es un conjunto no vacío de vectores V, dotado de dos operaciones binarias (suma de vectores y multiplicación por un escalar) que cumplen ciertas propiedades específicas.

También se le conoce como espacio lineal o espacio vectorial sobre K.

Visualmente, un espacio vectorial es el conjunto de todos los vectores que parten de un punto específico, junto con las operaciones de suma de vectores y multiplicación escalar.

Nota. Intuitivamente, los elementos de un espacio vectorial son vectores. No obstante, un espacio vectorial también puede estar constituido por otros objetos, como un conjunto de matrices o de polinomios.

¿Cuáles son los componentes de un espacio vectorial?

Los componentes de un espacio vectorial son los siguientes:

• Un campo (K), cuyos elementos se llaman escalares.
• Un conjunto no vacío (V), cuyos elementos se llaman vectores.
• Dos operaciones binarias: suma de vectores y multiplicación escalar, que satisfacen las siguientes propiedades:
  • Propiedad conmutativa $$ \vec{v}+\vec{w}=\vec{w}+\vec{v} \ \ \ \ \ \ \vec{v}, \vec{w} \in V $$
  • Propiedad asociativa $$ ( \vec{u}+\vec{v} ) +\vec{w} = \vec{u} + ( \vec{v}+\vec{w} ) \ \ \ \ \ \ \vec{v}, \vec{w}, \vec{u} \in V $$
  • Existencia del vector cero $$ \exists \ \vec{0} \ \in V \ \ | \ \ \vec{v}+\vec{0} = \vec{0}+\vec{v} = \vec{v} $$
  • Existencia de un inverso aditivo $$ \forall \ \vec{v} \ \ \exists \ -\vec{v} \ \in V \ \ | \ \ \vec{v}+(-\vec{v}) = \vec{0} $$
  • Multiplicación escalar $$ (a \cdot b) \cdot \vec{v} = a \cdot (b \cdot \vec{v} ) \ \ \ \ a,b \in K \ \ \ \vec{v} \in V $$

    Nota. El símbolo de multiplicación representa dos operaciones diferentes. El producto a*b es una multiplicación entre dos escalares en el campo K, mientras que (a*b)*v es la multiplicación de un escalar (a*b) por un vector v.

  • Propiedad distributiva $$ (a + b) \cdot \vec{v} = a \cdot \vec{v} + b \cdot \vec{v} \ \ \ \ \ \ \ \ a,b \in K \ \ \ \vec{v} \in V $$ $$ a \cdot (\vec{v} + \vec{w}) = a \cdot \vec{v} + a \cdot \vec{w} \ \ \ \ \ \ \ \ a \in K \ \ \ \vec{v}, \vec{w} \in V $$
  • Elemento neutro de la multiplicación escalar $$ 1 \cdot \vec{v} = \vec{v} \ \ \ \ \ \ \ \ \forall \vec{v} \in V $$

Es importante señalar que las propiedades de las operaciones en el espacio vectorial V son similares, aunque distintas, a las propiedades de las operaciones en el campo K.

En el espacio vectorial V, las operaciones se realizan entre vectores o entre vectores y escalares, mientras que en el campo K, las operaciones ocurren únicamente entre escalares.

Por lo tanto, en un espacio vectorial, las operaciones entre escalares deben cumplir las propiedades del campo K, mientras que las operaciones que involucran vectores deben satisfacer las propiedades del espacio vectorial V.

Para un análisis más detallado de las propiedades de las operaciones en un espacio vectorial, consulta la sección correspondiente.

¿Qué es un campo? En matemáticas, un campo es una estructura algebraica que consiste en un conjunto no vacío K y dos operaciones binarias (suma y multiplicación) representadas por + y *.

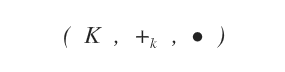
Si el campo K es el conjunto de los números reales R, el espacio se llama espacio vectorial real. Si el campo es el conjunto de los números complejos C, el espacio se denomina espacio vectorial complejo.

Un ejemplo de espacio vectorial

Ejemplo 1: El espacio vectorial R¹

El espacio vectorial R¹ es un espacio unidimensional (n=1) sobre el campo de los números reales K=R, donde se definen las operaciones de suma de vectores y multiplicación escalar.

Ya que n=1, el espacio vectorial es idéntico al campo de los números reales.

$$ R^1 = \{ (a_1) \} \ \ \ \ \ \ a_1 \in R $$

Cada punto en la recta representa un número real.

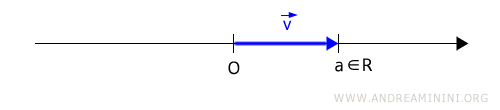
Con un origen fijo (O), cada punto en la recta representa un vector cuya magnitud (módulo) es igual a un número real.

Nota. En el espacio vectorial R¹, todos los vectores tienen la misma dirección, están orientados en un sentido u otro, y presentan distintas longitudes (módulos).

Aquí algunos ejemplos de vectores en R¹:

$$ \vec{v_1} = 3 \ \ \ \ \vec{v_2} = 5 \ \ \ \ \vec{v_3} = -1 \ \ \ ... $$

Las operaciones de suma de vectores y multiplicación escalar en R¹ cumplen con las propiedades de los espacios vectoriales.

Ejemplo 2: El espacio vectorial R²

Cuando n=2, el espacio vectorial R² (es decir, RxR) corresponde al plano cartesiano de los números reales.

$$ R^2 = \{ (a_1,a_2) \} \ \ \ \ \ \ a_1,a_2 \in R $$

Aquí, RxR es el producto cartesiano del conjunto de los números reales.

En este caso, cada par de números reales (x,y) representa un punto en la geometría euclidiana, o sea, un vector bidimensional.

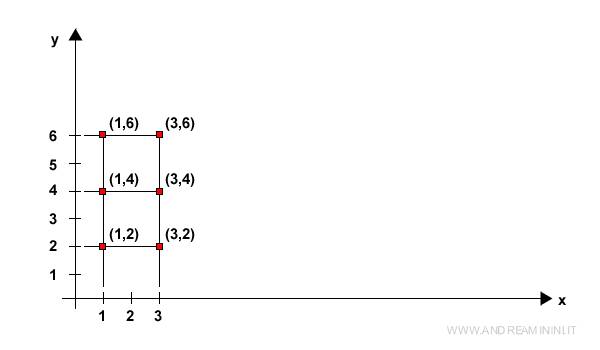
Así, el espacio vectorial real está compuesto por vectores en R².

Aquí algunos ejemplos de vectores con n=2 elementos en el campo de los números reales R:

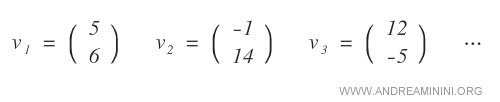
Nota. Dado que el conjunto de números reales R es infinito, el espacio vectorial real R² también es infinito.

En el espacio vectorial R² se definen dos operaciones binarias: la suma de vectores y la multiplicación escalar.

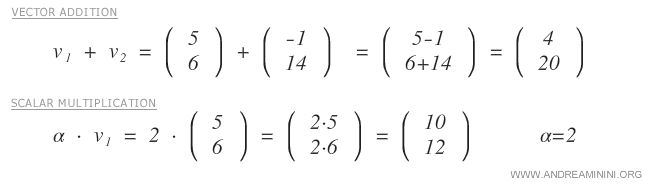
Todas las operaciones cumplen con las propiedades de los espacios vectoriales.

Esto demuestra que R² es un espacio vectorial sobre el campo R.

El mismo razonamiento se aplica a cualquier otro espacio vectorial real con vectores de dimensión n en Rⁿ.

Ejemplo 3: El espacio vectorial R³

Si n=3, el espacio vectorial R³ (es decir, RxRxR) corresponde al espacio tridimensional.

$$ R^3 = \{ (a_1,a_2, a_3) \} \ \ \ \ \ \ a_1,a_2, a_3 \in R $$

En este caso, cada tripleta de números reales (x,y,z) representa un punto en el espacio, es decir, un vector tridimensional donde a₁=x, a₂=y, a₃=z.

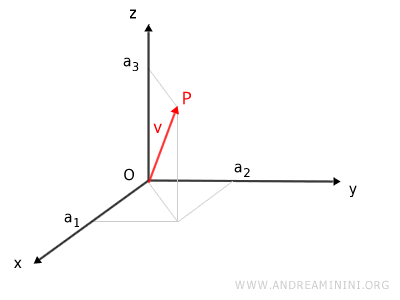
Además, en el espacio vectorial R³ se definen las dos operaciones binarias: la suma de vectores y la multiplicación escalar.

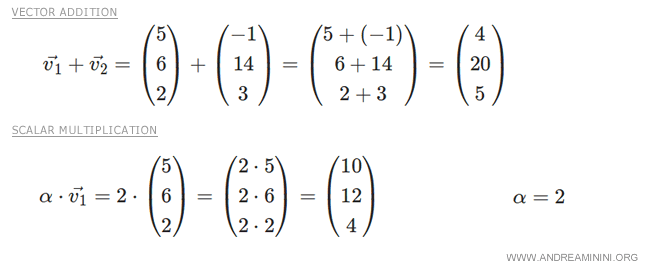
Las operaciones cumplen con todas las propiedades de los espacios vectoriales.

Ejemplo 4: El espacio vectorial R⁴

Para n=4, el espacio vectorial R⁴ (es decir, RxRxRxR) es un espacio de cuatro dimensiones.

Es un espacio compuesto por vectores con cuatro componentes (a₁, a₂, a₃, a₄).

$$ R^4 = \{ (a_1,a_2, a_3, a_4) \} \ \ \ \ \ \ a_1,a_2, a_3, a_4 \in R $$

 

En el espacio vectorial R⁴ se definen las dos operaciones binarias (suma de vectores y multiplicación escalar), y estas cumplen con todas las propiedades de los espacios vectoriales.

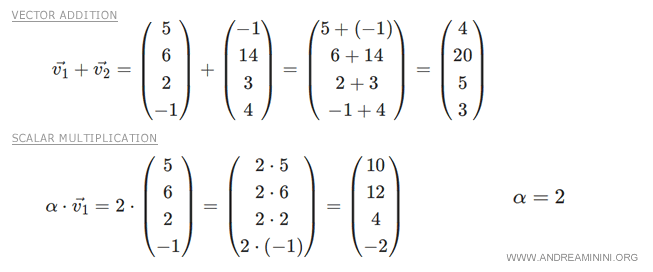
Nota. Imaginar un espacio vectorial de cuatro dimensiones o más puede ser difícil, ya que estamos acostumbrados a vivir en un espacio geométrico tridimensional. Es más fácil conceptualizar espacios con menos dimensiones (1 o 2) que uno de cuatro dimensiones. Sin embargo, los espacios vectoriales existen incluso en dimensiones mayores que tres.

Ejemplo 5: El espacio vectorial Rⁿ

El espacio vectorial Rⁿ es el producto cartesiano RxRx...xR, donde R se multiplica consigo mismo n veces.

$$ R^n = \{ (a_1, a_2, a_3, ... , a_n) \} \ \ \ \ \ \ a_i \in R $$

Cada elemento del espacio vectorial Rⁿ es un vector con n componentes, o sea, una n-tupla ordenada de números reales a₁, ..., a_n.

$$ \vec{v} = \begin{pmatrix} a_1 \\ a_2 \\ a_3 \\ \vdots \\ a_n \end{pmatrix} \ \ \ \ \ \ \ \vec{v} \in V = R^n $$

Por lo tanto, el espacio vectorial Rⁿ es el espacio de n-tuplas ordenadas en el campo K=R.

En el espacio vectorial Rⁿ se definen dos operaciones binarias:

1. La suma de dos vectores v₁ y v₂ da como resultado otro vector que pertenece al mismo espacio vectorial.
   
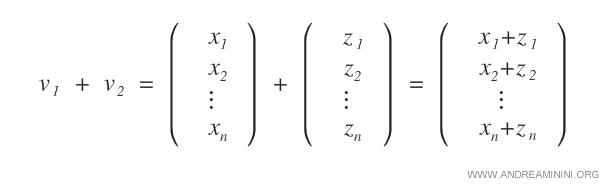
2. La multiplicación escalar de un escalar α con un vector v da como resultado otro vector que pertenece al mismo espacio vectorial.
   

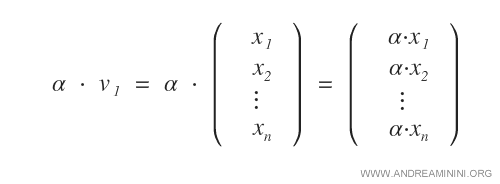
Las dos operaciones cumplen con todas las propiedades de un espacio vectorial.

Nota. Las propiedades (axiomas) de un espacio vectorial son las siguientes: asociativa, conmutativa, distributiva de la multiplicación sobre la suma de vectores, distributiva de la multiplicación sobre la suma escalar, existencia de un elemento neutro, existencia de un elemento inverso, compatibilidad de la multiplicación escalar, y compatibilidad del elemento neutro.

Norma y producto escalar

Los espacios vectoriales no incluyen inherentemente las nociones de longitud y ángulo de un vector.

Para introducir estos conceptos en los espacios vectoriales, se requiere una estructura adicional que consiste en dos entidades matemáticas:

• Norma. Es el concepto matemático que define la longitud (o magnitud) de un vector.
• Producto escalar. Es el concepto matemático que define el ángulo entre dos vectores.

Nota. Existen diversas estructuras para elegir, cada una con definiciones diferentes de norma y producto escalar. Por lo tanto, no hay una única definición posible del ángulo y la longitud de un vector.

Combinación lineal

Una de las operaciones más comunes en un espacio vectorial es la combinación lineal.

Una combinación lineal es una operación que involucra vectores y escalares dentro de un espacio vectorial V definido sobre el campo K=R. $$ \vec{w} = a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + a_3 \cdot \vec{v_3} + ... + a_n \cdot \vec{v_n} $$ Produce un vector (w) obtenido mediante la suma de productos entre n coeficientes escalares (a) y n vectores (v).

Donde w, v₁, v₂, ... ,v_n son vectores en el espacio vectorial V

$$ \vec{w}, \vec{v_1}, \vec{v_2}, ... , \vec{v_n} \in V $$

Mientras que los coeficientes a₁, a₂, ... , a_n son números (escalares), es decir, elementos del campo de los números reales K=R.

$$ a_1, a_2, ... , a_n \in K=R $$

Vectores linealmente dependientes e independientes

Las combinaciones lineales permiten determinar si los vectores en un espacio vectorial son:

• Vectores linealmente independientes
  Los vectores v₁, v₂,..., v_n son linealmente independientes si la única solución a su combinación lineal que da como resultado el vector cero $$ a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + ... + a_n \cdot \vec{v_n} = \vec{0} $$ es la combinación trivial donde todos los coeficientes escalares son cero, es decir, a_i= 0 $$ a_1 = a_2 = ... = a_n = 0 $$
• Vectores linealmente dependientes
  Los vectores v₁, v₂,..., v_n son linealmente dependientes si existe una o más soluciones no triviales para su combinación lineal que da como resultado el vector cero, donde al menos uno de los coeficientes escalares a_i ≠ 0 es distinto de cero. $$ a_1 \cdot \vec{v_1} + a_2 \cdot \vec{v_2} + ... + a_n \cdot \vec{v_n} = \vec{0} $$ En este caso, no todos los coeficientes a_i necesarios para obtener el vector cero son nulos. $$ \exists \ a_i \ne 0 $$

En esencia, dos o más vectores son linealmente dependientes entre sí cuando no son linealmente independientes.

Tipos de espacios vectoriales

Los espacios vectoriales se dividen en dos categorías:

• Espacios vectoriales finamente generados
  Son aquellos espacios vectoriales generados por un número finito de vectores.
• Espacios vectoriales infinitamente generados
  Son aquellos espacios vectoriales generados por un número infinito de vectores.

Y así sucesivamente.